Krychlička na nakloněné rovině
Úloha číslo: 764
Ve výšce h nad zemí je umístěna krychlička o hmotnosti m, která je nabita kladným nábojem o velikosti Q. Tuto krychličku necháme klouzat po nakloněné rovině, která se nachází v homogenním elektrickém poli o intenzitě \(\vec{E}\), jehož směr je zřejmý z obrázku.
Jaký úhel α musí svírat tato nakloněná rovina s vodorovným směrem, aby doba, za kterou se krychlička dostane na zem, byla co nejmenší?
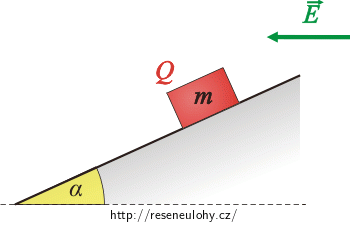
Tření mezi krychličkou a nakloněnou rovinou zanedbejte.
Nápověda: Působící síly
Na krychličku působí elektrická a tíhová síla a tlaková síla nakloněné roviny. Rozložte tyto síly na tečné a normálové složky.
Co musí platit pro normálové složky, aby se krychlička udržela na nakloněné rovině?
Které složky udávají zrychlení krychličky?
Nápověda: Vyjádření funkce času
K vyjádření závislosti času na sklonu nakloněné roviny využijte vztahu:
\[s\,=\,\frac{1}{2}at^2\,.\]Zrychlení krychličky závisí na působící síle a hmotnosti krychličky.
Délku nakloněné roviny můžeme vyjádřit pomocí výšky nakloněné roviny a úhlu, který svírá s vodorovnou rovinou.
Nápověda: Minimální čas
Minimum funkce nalezneme, položíme-li první derivaci funkce rovnu nule:
\[\frac{\mathrm{d}f}{\mathrm{d}\alpha}\,=\,0.\]Rozbor
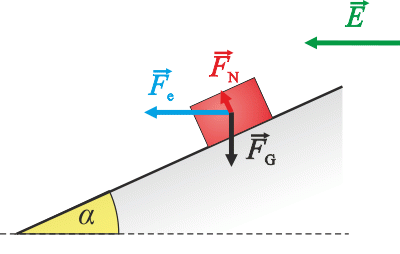
Na krychličku bude v průběhu pohybu působit tíhová a elektrická síla a tlaková síla nakloněné roviny.
Normálové složky sil
Aby se krychlička udržela na nakloněné rovině, musí být normálová složka tíhové síly větší než normálová složka síly elektrické nebo v kritickém případě jsou si rovny. (Případný rozdíl je kompenzován tlakovou silou nakloněné roviny.) Odtud získáme podmínku pro maximální velikost úhlu. Při větším úhlu se krychlička na nakloněné rovině neudrží a vlivem elektrické síly „odlétne“.
Poznámka: Obrázek je nakreslen pro mezní případ, kdy je tlaková síla nakloněné roviny nulová.
Tečné složky
Tečné složky obou sil udělují krychličce zrychlení ve směru nakloněné roviny. Jeho velikost můžeme vypočítat z druhého Newtonova zákona.
Poznámka: V tuto chvíli se zdá, že aby krychlička ujela svou dráhu za nejkratší čas, musí mít maximální zrychlení. Pozor, není tomu tak. V této úloze je dána výška, ve které se krychlička nachází. Měníme-li úhel nakloněné roviny, mění se také dráha, kterou krychlička musí urazit. Může se tedy stát, že krychlička bude mít minimální čas proto, že musela urazit menší dráhu, a ne proto, že měla velké zrychlení.
Minimální čas
Čas, za který krychlička sjela z nakloněné roviny, můžeme vyjádřit pomocí zrychlení a dráhy, kterou krychlička urazí. Získáme tak závislost času na úhlu, který svírá nakloněná rovina s vodorovnou rovinou. Pak už stačí najít minimum funkce pomocí první derivace.
Řešení: Vyjádření času
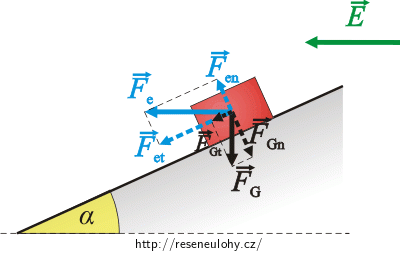
Na krychličku bude v průběhu pohybu působit tíhová síla \(\vec{F}_\mathrm{G}\), elektrická síla \(\vec{F}_\mathrm{e}\) a tlaková síla podložky \(\vec{F}_\mathrm{N}\). Tyto síly si rozložíme na tečnou a normálovou složku. Všimněme si, že normálové složky tíhové síly FGn a elektrické síly Fen mají opačný směr!
Poznámka: Obrázek je nakreslen pro mezní případ, kdy je tlaková síla nakloněné roviny nulová.
Aby se krychlička udržela na nakloněné rovině a klouzala dolů, je třeba, aby normálová složka síly tíhové byla větší nebo stejně velká jako normálová složka síly elektrické, jejich rozdíl je kompenzován tlakovou silou nakloněné roviny. V mezním případě jsou si normálové složky tíhové a elektrické síly rovny. Platí:
\[F_\mathrm{Gn}\,\geq \,F_\mathrm{en},\] \[mg\cos \alpha \,\geq \,QE \sin\alpha,\] \[\frac{\sin\alpha}{\cos \alpha} \,\leq \,\frac{mg}{QE},\] \[\mathrm{tg}\alpha \,\leq \,\frac{mg}{QE}.\tag{*}\]To znamená, že se krychlička udrží na nakloněné rovině pro úhly menší, než je maximální úhel:
\[\mathrm{tg}\alpha_\mathrm{m} \,= \,\frac{mg}{QE}.\]Tečné složky obou uvažovaných sil udělují krychličce pohybující se po nakloněné rovině zrychlení. To bude konstantní vzhledem k homogenitě tíhového pole Země i pole elektrického. Pro jeho velikost platí vztah:
\[a\,=\,\frac{F}{m},\] \[a\,=\,\frac{F_\mathrm{Gt}+F_\mathrm{et}}{m}\,=\,\frac{mg\sin\alpha+EQ\cos\alpha}{m},\] \[a\,=\,g\sin\alpha\,+\,\frac{EQ\cos\alpha}{m}.\tag{1}\]Krychlička se tedy bude po nakloněné rovině pohybovat rovnoměrně zrychleně; uvažujme, že s nulovou počáteční rychlostí. Pro dráhu při tomto typu pohybu platí vztah
\[s\,=\,\frac{1}{2}at^2\,.\]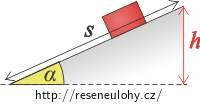
Odtud vyjádříme hledaný čas t:
\[t^2\,=\,\frac{2s}{a}.\tag{2}\]Poznámka: Dráha nakloněné roviny se s úhlem mění, proto ji musíme vyjádřit pomocí výšky nakloněné roviny, která zůstává stejná.
Pro celkovou délku s nakloněné roviny platí vzorec \(s\,=\,\frac{h}{\sin \alpha}\). Tento vzorec dosadíme spolu s vyjádřením zrychlení (1) do vztahu pro čas (2):
\[t^2\,=\,\frac{2\frac{h}{\sin \alpha}}{g\sin\alpha\,+\,\frac{EQ\cos\alpha}{m}},\] \[t^2\,=\,\frac{2h}{\sin \alpha\left(g\sin\alpha\,+\,\frac{EQ\cos\alpha}{m}\right)}.\] Nalezli jsme předpis funkce udávající závislost druhé mocniny doby potřebné k proběhnutí nakloněné roviny na úhlu α, jenž tato rovina svírá s vodorovným směrem.Řešení: Hledání minima
V předchozím oddíle jsme nalezli předpis funkce udávající závislost druhé mocniny doby potřebné k proběhnutí nakloněné roviny na úhlu α, jenž tato rovina svírá s vodorovným směrem:
\[t^2\,=\,\frac{2h}{\sin \alpha\left(g\sin\alpha\,+\,\frac{EQ\cos\alpha}{m}\right)}.\]Aby tato doba byla minimální, musíme určit takový úhel, při kterém bude výraz ve jmenovateli této funkce maximální (prostě hledáme extrém funkce úhlu α ve jmenovateli, čitatel je konstantní a nehraje tedy žádnou roli stejně jako fakt, že známe závislost druhé mocniny času).
Pozn.: Je samozřejmě možné celý zlomek odmocnit a derivovat takto získanou funkci. Derivování by bylo ale mnohem složitější a dostali bychom se ke stejnému výsledku.
Jmenovatele proto derivujeme podle α a derivaci položíme rovnu nule:
\[\frac{\mathrm{d}f}{\mathrm{d}\alpha}\,=\,0.\]Derivujeme jako součin:
\[\cos\alpha\left(g\sin\alpha\,+\,\frac{EQ}{m}\cos\alpha\right)\,+\,\sin\alpha \left(g\cos\alpha\,-\,\frac{EQ}{m}\sin\alpha\right)\,=\,0.\]Upravíme:
\[2g\sin \alpha \cos\alpha\, +\, \frac{EQ}{m} \left(\cos^2 \alpha - \sin^2\alpha \right)\,=\,0\]a použijeme vzorce pro goniometrické funkce dvojnásobného úhlu:
\[g\sin 2\alpha \, +\, \frac{EQ}{m}\cos 2\alpha \,=\,0.\]Upravíme a vyjádříme hledaný úhel α:
\[g\sin 2\alpha \, =\, -\frac{EQ}{m}\cos 2\alpha,\] \[\mathrm{tg}\,2\alpha \,=\,-\frac{EQ}{mg}.\]Vzhledem k tomu, že funkce tangens je lichá a periodická s periodou π, můžeme řešení psát ve tvaru:
\[ \alpha \,=\,\frac{1}{2}\left(n\pi- \,\mathrm{arctg}\,\frac{EQ}{mg}\right),\]kde n je libovolné celé číslo. A protože nás zajímá řešení v intervalu \((0,\,\pi/2)\), je hledaným kořenem
\[ \alpha \,=\,\frac{\pi}{2}- \frac{1}{2}\,\mathrm{arctg}\,\frac{EQ}{mg}.\]Ještě bychom měli ověřit matematicky pomocí druhé derivace, že se jedná skutečně o maximum. Plyne to i z fyzikálního rozboru úlohy: při větším úhlu je příspěvek elektrické síly do směru pohybu menší a krychličku urychluje hlavně tíhová síla, při malých úhlech je zase malý příspěvek tíhové síly, ale hlavně se prodlužuje délka nakloněné roviny.
Nyní je ještě nutné zkontrolovat, zda námi určený úhel splňuje podmínku, kterou jsme zformulovali na počátku, tj. že se krychlička při tomto úhlu udrží na nakloněné rovině. Tato podmínka pro maximální úhel zněla
\[\mathrm{tg}\, \alpha_\mathrm{m} \,= \,\frac{mg}{QE}.\]Dosadíme tuto podmínku do vztahu pro úhel α nejrychlejšího skouznutí dolů:
\[\alpha \,=\,\frac{\pi}{2}- \frac{1}{2}\,\mathrm{arctg}\,\frac{EQ}{mg} = \frac{\pi}{2}- \frac{1}{2}\,\mathrm{arccotg}\,\frac{mg}{EQ} =\] \[=\frac{\pi}{2}- \frac{1}{2}\,\mathrm{arccotg}\,\,(\mathrm{tg}\,{\alpha_\mathrm{m}}) = \frac{\pi}{2}- \frac{1}{2}\,\left(\frac{\pi}{2} - \mathrm{arctg}\,\,\mathrm{tg}\,{\alpha_\mathrm{m}}\right) = \] \[ = \frac{\pi}{2}- \frac{1}{2}\,\left(\frac{\pi}{2} - {\alpha_\mathrm{m}}\right) =\frac{\pi}{4} + \alpha_\mathrm{m}. \]Z předchozího výpočtu je vidět, že úhel, při kterém se krychlička dostane dolů nejrychleji, je větší než mezní úhel, při kterém se ještě krychlička udrží na nakloněné rovině.
Pokud by se tedy jednalo například o korálek navlečený na šikmé tyčce, potom by nejrychleji sklouznul dolů pod vypočteným úhlem α. V případě krychličky je ale pro nejrychlejší pohyb dolů nejlepší nastavit mezní úhel αm.
Odpověď
Krychlička vázaná na nakloněnou rovinu se dostane na zem v nejkratším čase, pokud nakloněná rovina svírá se svislým směrem úhel
\[ \alpha \,=\, \frac{\pi}{2}- \frac{1}{2}\,\mathrm{arctg}\,\frac{EQ}{mg}\,.\]Pokud je krychlička na nakloněnou rovinu volně položena, tak se při výše uvedeném úhlu na nakloněné rovině neudrží a pro sklouznutí v co možná nejkratším čase je třeba nastavit mezní úhel
\[ \alpha_\mathrm{m} \,=\, \mathrm{arctg}\,\frac{mg}{EQ}\,.\]Jak by se úloha změnila při konstantní délce nakloněné roviny
Podíváme se, jak by se řešení úlohy změnilo, pokud bychom neměli zadanou výšku, ve které se krychlička nachází, ale byla by zadaná dráha, kterou musí krychlička urazit, aby se dostala na zem.
Podmínka pro maximální úhel by byla stejná jako při původním zadání:
\[\mathrm{tg}\alpha_\mathrm{m} \,= \,\frac{mg}{QE}.\]Opět bychom pomocí tečných složek sil vypočítali zrychlení krychličky (viz vzorec (1) v části řešení Vyjádření času):
\[a\,=\,g\sin\alpha\,+\,\frac{EQ\cos\alpha}{m}.\]Stejně bychom vyjádřili také čas pomocí dráhy a zrychlení (viz vzorec (2)):
\[t^2\,=\,\frac{2s}{a}.\]Nyní se postup řešení trochu liší. Protože máme zadanou dráhu, která se nemění, můžeme z tohoto vzorce zjistit, za jakých podmínek bude čas minimální.
Protože v čitateli zlomku jsou pouze konstanty, záleží velikost zlomku pouze na jeho jmenovateli, tzn. na zrychlení. Aby byl zlomek minimální, musí být zrychlení maximální.
Pomocí první derivace tedy zjistíme maximum zrychlení:
\[\frac{\mathrm{d}a}{\mathrm{d}\alpha}\,=\,0,\] \[\frac{\mathrm{d}}{\mathrm{d}\alpha}\left(g\sin\alpha\,+\,\frac{EQ\cos\alpha}{m} \right)\,=\,0,\] \[g\cos\alpha\,-\,\frac{EQ\sin\alpha}{m}\,=\,0.\]Funkce úhlu převedeme na jednu stranu rovnice:
\[g\cos\alpha\,=\,\frac{EQ\sin\alpha}{m},\] \[\frac{\sin\alpha}{\cos\alpha}\,=\,\frac{mg}{EQ}.\]Stejný vztah jsme dostali pro mezní úhel. Krychlička tedy urazí dráhu za minimální čas při maximálním úhlu, který může nakloněná rovina svírat s vodorovnou rovinou, aby se krychlička na rovině udržela. Pro tento úhel platí vztah:
\[\mathrm{tg}\, \alpha_\mathrm{m} \,= \,\frac{mg}{QE}.\]