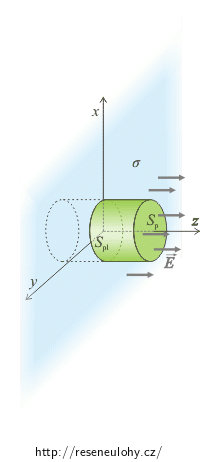
Pole rovnoměrně nabité roviny
Úloha číslo: 443
Na nekonečné rovinné desce je rovnoměrně rozmístěn náboj s plošnou hustotou σ.
1) Určete intenzitu elektrického pole ve vzdálenosti z od roviny.
2) Najděte také elektrický potenciál ve vzdálenosti z od roviny.
Nápověda: Intenzita elektrického pole
Protože k řešení úlohy se hodí využít Gaussovu větu, je třeba si rozmyslet, jakou Gaussovu plochu zvolíme.
Vhodnou plochou je povrch válce, jehož osa je kolmá k rovině a rovina prochází jeho středem. Rozmyslete si, jaká je poloha vektoru intenzity vzhledem k podstavám a plášti válce.
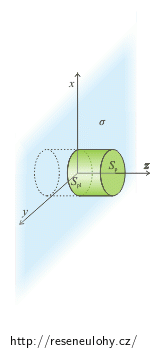
Celkový tok Gaussovou plochou získáme sečtením toku pláštěm a oběma podstavami válce.
Nápověda: Elektrický potenciál
Potenciál je potenciální energie vztažená na jednotkový náboj
\[\varphi\,=\, \frac{E_\mathrm{p}}{Q}\]a potenciální energie je rovna záporně vzaté práci, kterou musí vykonat elektrická síla, aby přenesla náboj z místa s nulovou potenciální energií (označme ho třeba A) do daného místa (označme ho B):
\[E_\mathrm{p}(z)\,=\, - \int_\mathrm{A}^\mathrm{B} \vec{F} \cdot \mathrm{d}\vec{z}.\]Vydělíme obě strany nábojem Q a dostaneme:
\[\varphi\,=\, - \int_\mathrm{A}^\mathrm{B} \frac{\vec{F}} {Q}\cdot \mathrm{d}\vec{z}.\]Jestliže sílu \(\vec{F}\) vydělíme nábojem Q, získáme intenzitu elektrického pole \(\vec{E}\):
\[\varphi\,=\, - \int_\mathrm{A}^\mathrm{B} \vec{E}\cdot \mathrm{d}\vec{z}.\]Rozbor
Vzhledem k symetrickému rozložení náboje je nejjednodušším způsobem nalezení intenzity elektrického pole v tomto případě využití Gaussovy věty. Gaussova věta vyjadřuje vztah mezi tokem elektrické intenzity uzavřenou plochou a celkovým nábojem, který se nachází uvnitř této plochy.
Vektory elektrické intenzity jsou ve všech místech kolmé na rovinu a jejich velikost závisí pouze na vzdálenosti od roviny. (V závislosti na znaménku náboje míří vektory buď směrem k rovině, nebo směrem od ní.) Důvodem je symetrické rozložení náboje. Vzhledem k symetrii úlohy můžeme také celou úlohu vyřešit pouze pro kladné hodnoty z, pro záporné hodnoty se změní pouze směr vektoru.
Jako Gaussovu plochu volíme povrch válce jehož osa je kolmá na rovinu desky a zároveň prochází nabitá rovina středem válce. V tomto případě je vektor elektrické intenzity kolmý na podstavy válce a zároveň rovnoběžný s pláštěm válce. Tím se nám zjednoduší výpočet toku elektrické intenzity jeho povrchem.
Celkový tok intenzity Gaussovou plochou získám sečtením toku pláštěm válce a oběma podstavami válce.
Potenciál vypočítáme z elektrické intenzity. Potenciál v daném místě se až na znaménko rovná integrálu intenzity z místa s nulovým potenciálem do tohoto místa.
Řešení: Intenzita
Intenzitu elektrického pole nabité roviny vyjádříme pomocí Gaussovy věty:
\[\oint_\mathrm{S} \vec{E} \cdot \mathrm{d}\vec{S}\,=\, \frac{Q}{\varepsilon_0},\] \[\oint_\mathrm{S} \vec{E} \cdot \vec{n}\mathrm{d}S\,=\, \frac{Q}{\varepsilon_0}.\]Protože je náboj na rovině rozložen symetricky, je také elektrické pole v okolí roviny symetrické. Vektor elektrické intenzity je ve všech místech kolmý na rovinu a jeho velikost závisí pouze na vzdálenosti z od roviny.
Pozn.: Na obrázku je nabitá rovina totožná s rovinou xy a je vyznačena modrou barvou.
Jako Gaussovu plochu volíme povrch válce, jehož osa je k rovině kolmá. Plochu volíme takto proto, že vektor intenzity je kolmý k podstavám válce a rovnoběžný s pláštěm válce (viz obrázek), což zjednoduší výpočet skalárního součinu. (Obecný postup Jak volit Gaussovu plochu je popsán v úloze Pole rovnoměrně nabité koule.)
Celkový tok intenzity povrchem válce získáme sečtením toku pláštěm a oběma podstavami. Protože obě podstavy válce mají od nabité roviny stejnou vzdálenost, je velikost intenzity na obou podstavách stejná. Indukční tok oběma podstavami je stejný, a proto tok podstavou započítáváme do celkového toku intenzity dvakrát. Upravíme tedy levou stranu Gaussovy věty:
\[\oint_\mathrm{Spl} \vec{E} \cdot \vec{n}\mathrm{d}S\,+2\oint_\mathrm{Sp} \vec{E} \cdot \vec{n}\mathrm{d}S\,=\, \frac{Q}{\varepsilon_0}.\tag{*}\]Tok pláštěm:
Vektor intenzity je rovnoběžný s pláštěm válce, a tedy kolmý na normálový vektor této plochy. Proto je skalární součin obou vektorů roven nule, a tedy i tok intenzity pláštěm válce je nulový:
\[\oint_\mathrm{Spl} \vec{E} \cdot \vec{n}\mathrm{d}S\,=\, 0.\]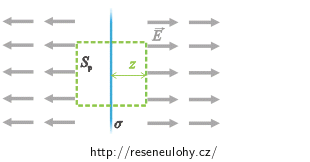
Tok podstavou:
Vektor intenzity je ve všech místech podstavy k ní kolmý (a tedy rovnoběžný s normálovým vektorem), proto můžeme skalární součin zjednodušit:
\[ \vec{E} \cdot \vec{n} \,=\, En\,=\,E\](pozn.: \(\vec{n}\) je jednotkový vektor).
S využitím těchto poznatků upravíme integrál na levé straně Gaussovy věty a vyjádříme tok podstavou válce:
\[\oint_\mathrm{Sp} \vec{E} \cdot \vec{n}\mathrm{d}S\,=\,\oint_\mathrm{Sp} E n\mathrm{d}S\,=\, \oint_\mathrm{Sp} E\mathrm{d}S.\]Velikost vektoru elektrické intenzity E je ve všech místech podstavy stejná, a proto ji můžeme vyjmout před integrál jako konstantu. Dostáváme tedy vztah:
\[\oint_\mathrm{Sp} \vec{E} \cdot \vec{n}\mathrm{d}S\,=\,E \oint_\mathrm{Sp} \mathrm{d}S\,=\,E S_\mathrm{p},\]kde Sp je obsah podstavy Gaussova válce.
Výsledný vztah dosadíme zpět do Gaussovy věty (*). Nesmíme zapomenout, že válec má podstavy dvě, proto musíme tok podstavou započítat dvakrát:
\[2 E S_\mathrm{p}\,=\, \frac{Q}{\varepsilon_0}.\]Zbývá vyjádřit náboj Q uvnitř Gaussovy plochy. Uvnitř válce je část desky o obsahu Sp. Náboj vyjádříme pomocí obsahu této části a plošné hustoty náboje Q = σSp:
\[2 E S_\mathrm{p}\,=\, \frac{\sigma S_\mathrm{p}}{\varepsilon_0}.\]Vyjádříme velikost intenzity elektrického pole nabité desky:
\[E \,=\, \frac{\sigma}{2 \varepsilon_0}.\]Vypočítali jsme, že velikost intenzity nezávisí na vzdálenosti od nabité roviny. Nekonečná nabitá rovina kolem sebe vytváří homogenní pole.
Řešení: Potenciál
Potenciál v bodě A, který je ve vzdálenosti z od roviny, se až na znaménko rovná integrálu intenzity z místa s nulovým potenciálem do bodu A. (Podrobnější vysvětlení je uvedeno v nápovědě.) Velmi často volíme nulový potenciál v nekonečnu, zkusme to i v této úloze:
\[\varphi (z)\,=\, - \int_{\infty}^\mathrm{z} \vec{E} \cdot \mathrm{d}\vec{z}.\]Potenciál nezávisí na volbě integrační cesty, proto ji můžeme volit libovolně. V této úloze jako integrační cestu zvolíme část přímky, která je kolmá na rovinu.
Vektor elektrické intenzity \(\vec{E}\) je rovnoběžný s vektorem \(\vec{z}\), proto můžeme integrál zjednodušit:
\[\varphi (z)\,=\, - \int^\mathrm{z}_{\infty} E \mathrm{d}z. \]Protože velikost elektrické intenzity je konstantní, můžeme intenzitu vyjmout před integrál:
\[\varphi (z)\,=\, - E \int^\mathrm{z}_{\infty} \mathrm{d}z. \]Vypočítáme určitý integrál:
\[\varphi (z)\,=\, - E \,[z]^\mathrm{z}_\infty. \]Z výsledku vidíme, že volba nulového potenciálu v nekonečnu není vhodná, protože integrál „nelze dopočítat“. Zkusíme tedy zvolit nulový potenciál přímo na nabité rovině, tedy pro z = 0. V integrálu se změní pouze dolní mez:
\[\varphi (z)\,=\, - E \int^\mathrm{z}_{0} \mathrm{d}z \,=\, - E \,[z]^z_0 \,=\, - E z. \]Nyní už jsme integrál dopočítat mohli, volba nulového potenciálu na rovině je tedy vhodná. (Pozn.: Podobné „problémy“ s volbou místa s nulovou hodnotou potenciálu v nekonečnu nastávají u všech těles, která „zasahují nabitou plochou až do nekonečna“.)
Dosadíme velikost elektrické intenzity, kterou jsme si vyjádřili v předchozím oddíle:
\[\varphi (z) \,=\,- \,\frac{\sigma }{2 \varepsilon_0}\,z.\]Potenciál je největší na nabité desce a poté se vzdáleností od desky lineárně klesá.
Protože jsme úlohu řešili pouze na jedné straně roviny, tj. pro z > 0, je třeba si uvědomit, že na druhé straně roviny je situace obdobná a i zde bude potenciál lineárně klesat. Pokud budeme z chápat jako vzdálenost od roviny, pak získaný vztah platí pro všechna místa. Pokud ale chceme z chápat jako souřadnici, je třeba do získaného vztahu doplnit absolutní hodnotu:
\[\varphi (z) \,=\,- \,\frac{\sigma }{2 \varepsilon_0}\,|z|.\]Odpověď
Nabitá nekonečná rovina kolem sebe vytváří homogenní pole o intenzitě
\[E (z) \,=\,\frac{\sigma }{2 \varepsilon_0}\,.\]Vektory elektrické intenzity jsou ve všech místech kolmé na rovinu a míří buď směrem od roviny v případě kladného náboje, nebo k rovině při záporném náboji na rovině.
Potenciál elektrického pole roviny je největší na nabité rovině a poté se vzdáleností od roviny na obě strany lineárně klesá (při kladném náboji):
\[\varphi (z) \,=\,- \,\frac{\sigma }{2 \varepsilon_0}\,|z|.\]Pozn.: Nyní už bereme z jako souřadnici a ne jako vzdálenost od roviny.
Grafy
Při kreslení grafů uvažujeme, že je rovina nabita kladným nábojem.
Graf závislosti velikosti el. intenzity na vzdálenosti od roviny
Velikost elektrické intenzity je konstantní: \(E\,=\,\frac{\sigma}{2 \varepsilon_0}.\)
Grafem je tedy konstantní funkce, která je na kladné části osy z kladná a na záporné části osy záporná. Je to proto, že vektor elektrické intenzity má „za rovinou“ opačný směr než „před rovinou“.
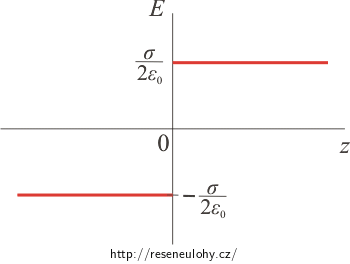
Pozn.: Intenzita elektrického pole je spojitá s výjimkou bodů, kdy prochází nabitou plochou. Při průchodu nabitou plochou zůstávají spojité pouze tečné složky vektoru. Normálové složky se mění „skokem“, který je úměrný plošné hustotě náboje, což v našem případě platí.
Graf závislosti el. potenciálu na vzdálenosti od roviny
Potenciál je největší na nabité desce, tj. pro z = 0.
Poté se vzdáleností od desky na obě strany lineárně klesá:
\[\varphi (z)\,=\,- \,\frac{\sigma}{2 \varepsilon_0}\,|z|.\]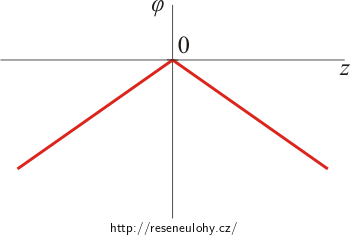
Pozn.: Elektrický potenciál je vždy spojitý, protože se jedná vlastně o práci při přenášení jednotkového náboje a ta se nemůže změnit „skokově“. Kromě nabitých ploch má potenciál spojité také první derivace, tj. je hladký.