Sbírka řešených úloh

Kondenzátor částečně vyplněný dielektrikem

Úloha číslo: 28

Vypočtěte výslednou kapacitu deskového kondenzátoru, jestliže prostor mezi jeho deskami o ploše S je zaplněn dielektrikem o permitivitě ε podle nákresu na obrázku.

• Nápověda: Jak začít

  Kondenzátor, který je takto z části vyplněn dielektrikem, můžeme nahradit dvěma paralelně zapojenými kondenzátory. Jeden bude vzduchový a druhý zcela vyplněný dielektrikem.

• Nápověda: Kapacita kondenzátoru

  Kapacity paralelně zapojených kondenzátorů se sčítají.

• Rozbor

  Deskový kondenzátor, který je takto z části vyplněn dielektrikem, můžeme nahradit dvěma paralelně zapojenými kondenzátory. Jeden bude vyplněný dielektrikem a druhý bude vzduchový.

  Celková kapacita paralelně zapojených kondenzátorů je rovna součtu kapacit těchto kondenzátorů.

  Kapacita deskového kondenzátoru závisí nepřímo úměrně na vzdálenosti desek a přímo úměrně na ploše kondenzátoru a permitivitě prostředí, které je mezi deskami.

  Jediné, co nám zbývá určit, jsou plochy desek obou kondenzátorů. Využijeme toho, že známe celkovou plochu kondenzátoru, a víme také, v jakém poměru délek se kondenzátor rozdělil na dva.

• Řešení

  Deskový kondenzátor si nahradíme dvěma kondenzátory zapojenými paralelně. Jeden vyplněný dielektrikem o šířce l₁ a druhý vzduchový o šířce l−l₁.

  

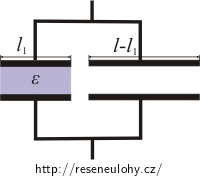
  Celková kapacita je tedy dána součtem kapacit těchto dvou kondenzátorů:

  \[C\,=\,C_1+C_2.\tag{1}\]

  Kapacita deskového kondenzátoru je dána vztahem:

  \[C\,=\, \epsilon \frac{S}{d}\,=\,\epsilon_0 \epsilon_r \frac{S}{d}.\]

  Pro kapacity našich kondenzátorů platí:

  \[C_1\,=\, \epsilon_0 \epsilon_r\frac{S_1 }{d},\tag{2}\] \[C_2\,=\,\epsilon_0 \frac{S_2 }{d}.\tag{3}\]

  Nyní si vyjádříme plochy S₁ a S₂ pomocí délek l, l₁ a celkové plochy kondezátoru S.

  Celková plocha kondenzátoru je:

  \[ S\,=\,lx\,\,\Rightarrow\,\,x\,=\,\frac{S}{l}\,,\tag{*}\]

  kde x jsme si označili šířku kondenzátoru.

  Plochy S₁ a S₂ můžeme vyjádřit podobně S₁ = l₁x a S₂ = (l-l₁)x.

  Dosadíme-li za x ze vztahu (*) získáme plochy desek obou kondenzátorů, které jsme potřebovali:

  \[S_1\,=\,\frac{l_1}{l}S,\] \[S_2\,=\,\frac{l-l_1}{l}S.\]

  Teď už zbývá jen dosadit plochy S₁ a S₂ do vzorců pro kapacity C₁ a C₂ (vzorec (2) a (3)) a vše dosadit do vztahu (1) pro celkovou kapacitu:

  \[C\,=\, \epsilon_0 \epsilon_r \frac{l_1 S}{dl} +\epsilon_0 \frac{\left(l-l_1\right) S}{dl}.\]

  Vytkneme zlomek \(\frac{\epsilon_0 S}{dl}\):

  \[C\,=\, \frac{\epsilon_0 S}{dl} \left( \epsilon_r l_1+l-l_1\right).\]

  Nakonec ještě uvnitř závorky můžeme vytknout l₁ a máme vztah pro celkovou kapacitu kondenzátoru C:

  \[C\,=\, \frac{\epsilon_0 S}{dl} \left(l_1 \left(\epsilon_r -1\right)+l\right).\]

• Odpověď

  Celková kapacita kondenzátoru je dána vztahem:

  \[C\,=\, \frac{\epsilon_0 S}{dl} \left(l_1 \left(\epsilon_r -1\right)+l\right)\,.\]

• Jinak vložené dielektrikum

  Zamyslete se nad tím, jak by se úloha řešila, kdyby bylo dielektrikum vloženo jinak (viz obrázek)?

  

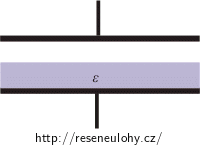
  Pokud by byl kondenzátor vyplněn dielektrikem tak, jak je znázorněno na obrázku, rozdělili bychom si ho opět na dva kondenzátory (vzduchový a kondenzátor s dielektrikem). V tomto případě by ale kondenzátory byly zapojeny sériově.