Sbírka řešených úloh

Nabité těleso na závěsu

Úloha číslo: 799

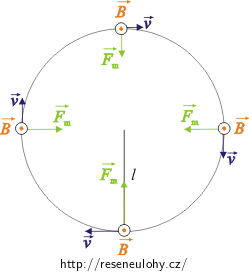
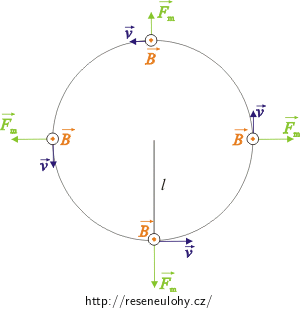
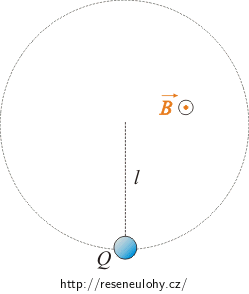
Malé těleso o hmotnosti m s kladným nábojem Q, které je připevněno k niti o délce l, se může pohybovat po kružnici ve vertikální rovině. Homogenní pole o magnetické indukci $\vec{B}$ je orientováno kolmo k této rovině a směřuje ven z nákresny. Jakou minimální rychlost musíme tělesu udělit ve spodním bodě, aby vykonalo celý obrat?

Poznámka: Jedná se v podstatě o kyvadlo.

• Nápověda 1

  Zamyslete se, jak určíte směr magnetické síly?

• Řešení nápovědy

  Řekněme, že budeme udělovat tělesu rychlost $\vec{v}$ ve směru pohybu hodinových ručiček (jak je znázorněno na obrázku).

  

  Magnetická síla $\vec{F}_\mathrm{m}$ je dána vztahem

  $$\vec{F}_\mathrm m=q\vec{v} \times \vec{B}.$$

  Z tohoto vztahu určíme směr magnetické síly. Vektory tvoří ve vztahu výše pravotočivou bázi, proto magnetická síla $\vec{F}_\mathrm{m}$ musí podle obrázku směřovat v každém bodě na trajektorii do středu otáčení.

• Nápověda 2

  Dále se tato úloha řeší stejnou strategií jako úloha Otáčející se nabitá kulička kolem druhé stejně nabité kuličky, ve které jsou úvahy převzaté z úlohy Koule přivázaná na konci provazu.

• Rozbor

  O tom, jestli kulička vykoná otočku, se rozhodne při průchodu nejvyšším bodem trajektorie. Proto si musíme uvědomit, jaké síly budou na kuličku v tomto bodě působit. Na kuličku bude působit síla tíhová, síla magnetická a také síla nitě; výslednice těchto sil se musí rovnat síle dostředivé. Pomocí 2. Newtonova zákona určíme minimální rychlost v tomto bodě.

  Minimální rychlost, udělenou v nejnižším bodě kruhové trajektorie, určíme ze zákona zachování mechanické energie.

• Řešení

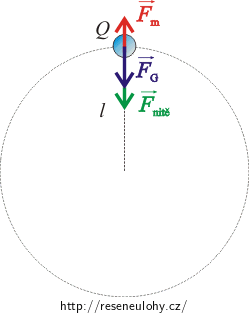
  Kritické místo pro dokončení otočky je nejvyšší bod trajektorie. Proto si musíme uvědomit, které síly budou na těleso v tomto bodě působit. Nakreslíme si obrázek.

  

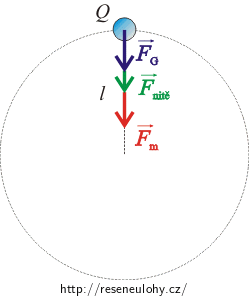
  Určitě se projeví síla tíhová $\vec{F}_\mathrm G$, která se bude snažit dokončení otáčky zabránit; dále síla magnetická $\vec{F}_\mathrm m$, jež bude působit stejným směrem jako síla tíhová, a nesmíme opomenout ani sílu nitě. Aby těleso otočku dokončilo, musí být výslednice těchto sil rovna síle dostředivé $\vec{F}_\mathrm {do}$. Síla nitě je v mezním případě v nejvyšším bodě trajektorie nulová. Všechny síly jsou v jedné přímce, proto pro velikost výslednice píšeme $$F_\mathrm {do}=F_\mathrm m+F_\mathrm G.$$ Jednotlivé síly vyjádříme a získáme vztah

  $$m\frac{{v_1}^2}{l}=B Q v_1+mg,$$

  kde v₁ je rychlost v nejvyšším bodě trajektorie. Rovnici si upravíme tak, aby u v₁² byl koeficient 1 a na pravé straně rovnice nula

  $$\frac{m}{l}{v_1}^2-B Q v_1-mg=0$$ $${v_1}^2-\frac{BQl}{m}-gl=0.$$

  Dostali jsme kvadratickou rovnici, z níž vypočteme minimální požadovanou rychlost tělesa v nejvyšším bodě trajektorie v_1:

  $$v_1=\frac{\frac{BQ}{m}\pm \sqrt{\frac{B^{2}Q^{2}l^2}{m^2}+4gl}}{2}=\frac{BQl}{2m}+\sqrt{\frac{B^2Q^2l^2}{4m^2}+gl}.$$

  Protože rychlost musí být v našem případě kladná, vyhovuje pouze řešení se znaménkem plus.

  My však nemáme určit v₁, nýbrž minimální rychlost udělenou na počátku pohybu, tedy v nejnižším bodě kruhové trajektorie. Tuto rychlost označme v_m a zamyslíme se, jak souvisí s již spočtenou v₁. Vyjdeme ze zákona zachování mechanické energie. Platí, že součet kinetické a potenciální tíhové energie soustavy je stálý. Při volbě hladiny nulové potenciální energie v nejnižším bodě trajektorie můžeme psát

  $$E_\mathrm {k1}+E_\mathrm p=E_\mathrm {km},$$

  kde E_k1 je kinetická a E_p potenciální energie tělesa v nejvyšším bodě, E_km označuje kinetickou energii v nejnižším bodě trajektorie. Tyto energie vyjádříme:

  $$\frac{1}{2}m v_1 ^{2} + 2 mgl=\frac{1}{2}m v_m ^{2}.$$

  Odtud vyjádříme minimální rychlost potřebnou na začátku pohybu v_m a to tak, že celou rovnici vynásobíme dvěma a vydělíme m. Poté celý výraz odmocníme:

  $$v_\mathrm m = \sqrt{v_1 ^{2}+4gl}.$$

  V tomto vztahu vystupuje kvadrát minimální požadované rychlosti v nejvyšším bodě trajektorie, tedy v₁², proto si ho nyní spočítáme:

  $$v_1 ^{2} =\left(\frac{BQl}{2m}+\sqrt{\frac{B^2Q^2l^2}{4m^2}+gl}\right)^2=\frac{B^2Q^2l^2}{4m^2}+2\frac{BQl}{2m}\cdot \sqrt{\frac{B^2Q^2l^2}{4m^2}+gl}+\frac{B^2Q^2l^2}{4m^2}+gl=$$ $$=gl+\frac{BQl}{m}\cdot \left(\frac{BQl}{2m}+\sqrt{\frac{B^2Q^2l^2}{4m^2}+gl}\right).$$

  Dosadíme do vztahu pro v_m a získáváme

  $$v_\mathrm m = \sqrt{5 g l+\frac{BQl}{m}\cdot \left(\frac{BQl}{2m}+\sqrt{\frac{B^2Q^2l^2}{4m^2}+gl}\right)}.$$

• Odpověď

  Minimální rychlost, kterou musíme tělesu udělit, je dána vztahem:

  $$v_\mathrm m = \sqrt{5 g l+\frac{BQl}{m}\cdot \left(\frac{BQl}{2m}+\sqrt{\frac{B^2Q^2l^2}{4m^2}+gl}\right)}.$$

• Jak by to vypadalo, kdybychom uvažovali opačný směr rychlosti

  Změnou směru rychlosti změníme i směr magnetické síly, což je ekvivalentní tomu, když ponecháme stejný směr pohybu a změníme znaménko u náboje Q.

• Podrobné provedení důkazu

  Situaci si nakreslíme:

  

  Nyní si nakreslíme jaké síly působí na těleso v nejvyšším bodě trajektorie.

  

  V nejvyšším bodě trajektorie na těleso působí stejné síly jako v námi uvažovaném řešení, pouze s tím rozdílem, že magnetická síla $\vec{F}_\mathrm m$ má opačný směr. S uvážením nulovosti síly nitě v mezním případě a toho, že síly leží v jedné přímce, můžeme pro velikost výslednice psát

  $$F_\mathrm {do}=F_\mathrm g-F_\mathrm m.$$

  Síly vyjádříme:

  $$m\frac{{v_1}^2}{l}=mg-B Q v_1.$$

  Dostáváme kvadratickou rovnici pro v₁. Tu si upravíme:

  $$\frac{m}{l}{v_1}^2+B Q v_1-mg=0$$ $${v_1}^2+\frac{BQl}{m}-gl=0.$$

  Dostali jsme kvadratickou rovnici, z níž vypočteme minimální požadovanou rychlost tělesa v nejvyšším bodě trajektorie v_1:

  $$v_1=\frac{-\frac{BQ}{m}\pm \sqrt{\frac{B^{2}Q^{2}l^2}{m^2}+4gl}}{2}=-\frac{BQl}{2m}+\sqrt{\frac{B^2Q^2l^2}{4m^2}+gl}.$$

  Protože rychlost musí být kladná, vyhovuje opět pouze řešení se znaménkem plus.

  Určení minimální rychlosti v_m provedeme stejným způsobem jako v našem původním řešení. Pro v_m získáváme proto stejný vztah

  $$v_\mathrm m = \sqrt{v_1 ^{2}+4gl}.$$

  Do tohoto vztahu potřebujeme kvadrát minimální rychlosti v nejvyšším bodě v₁², proto si ho nyní spočítáme:

  $$v_1 ^{2} =\left(-\frac{BQl}{2m}+\sqrt{\frac{B^2Q^2l^2}{4m^2}+gl}\right)^2=\frac{B^2Q^2l^2}{4m^2}-2\frac{BQl}{2m}\cdot \sqrt{\frac{B^2Q^2l^2}{4m^2}+gl}+\frac{B^2Q^2l^2}{4m^2}+gl=$$ $$=gl+\frac{BQl}{m}\cdot \left(\frac{BQl}{2m}-\sqrt{\frac{B^2Q^2l^2}{4m^2}+gl}\right).$$

  Dosadíme do vztahu pro v_m a získáváme

  $$v_\mathrm m = \sqrt{5 g l+\frac{BQl}{m}\cdot \left(\frac{BQl}{2m}-\sqrt{\frac{B^2Q^2l^2}{4m^2}+gl}\right)}.$$

  Odtud vidíme, že nám to opravdu vyšlo stejně, jako kdybychom změnili znaménko u náboje Q.