Pole nabitého válce
Úloha číslo: 444
Nekonečně dlouhý válec o poloměru R je rovnoměrně nabit nábojem s objemovou hustotou ρ.
1) Najděte vztah pro intenzitu elektrického pole ve vzdálenosti z od osy válce.
2) Určete také potenciál ve vzdálenosti z.
Uvažujte pole uvnitř i vně válce, tzn. najděte průběh elektrické intenzity a potenciálu pro z v intervalu „od nuly až do nekonečna“.
Nápověda: Intenzita elektrického pole
Protože k řešení úlohy se hodí využít Gaussovu větu, je třeba si rozmyslet, jakou Gaussovu plochu zvolíme.
Vhodnou plochou je povrch válce o poloměru z a výšce h, jehož osa splývá s osou nabitého válce. V takovém případě je vektor elektrické intenzity ve všech místech kolmý na plášť válce a rovnoběžný s podstavami. (Viz oddíl Jak volit Gaussovu plochu? v úloze Pole rovnoměrně nabité koule.)
Úlohu rozdělíme na dvě části:
- Poloměr Gaussova válce je větší než poloměr nabitého válce.
- Poloměr Gaussova válce je menší než poloměr nabitého válce.
Nápověda: Elektrický potenciál
Potenciál je roven potenciální energii vztažené na jednotkový náboj
\[\varphi\,=\, \frac{E_\mathrm{p}}{Q}\]a potenciální energie je rovna záporně vzaté práci, kterou musí vykonat elektrická síla, aby přenesla náboj z místa s nulovou potenciální energií (v našem případě zvolíme nulovou potenciální energii na povrchu válce) do daného místa:
\[E_\mathrm{p}(z)\,=\, - \int^\mathrm{z}_\mathrm{R} \vec{F} \cdot \mathrm{d}\vec{z}.\]Obě strany rovnice vydělíme nábojem Q a dostaneme:
\[\varphi\,=\, - \int^\mathrm{z}_\mathrm{R} \frac{\vec{F}} {Q}\cdot \mathrm{d}\vec{z}\,.\]Jestliže sílu \(\vec{F}\) vydělíme nábojem Q, získáme intenzitu elektrického pole \(\vec{E}\):
\[\varphi\,=\, - \int^\mathrm{z}_\mathrm{R} \vec{E}\cdot \mathrm{d}\vec{z}.\]Rozbor
Úlohu si rozdělíme na dvě části. Budeme zkoumat zvlášť pole uvnitř nabitého válce a zvlášť pole vně válce.
Vzhledem k symetrickému rozložení náboje je nejjednodušším způsobem nalezení intenzity elektrického pole v tomto případě využití Gaussovy věty. Gaussova věta vyjadřuje vztah mezi tokem elektrické intenzity uzavřenou plochou a celkovým nábojem, který se nachází uvnitř této plochy.
Vektor elektrické intenzity míří ve všech místech od osy válce směrem ven a jeho velikost závisí pouze na vzdálenosti od osy válce. Důvodem je symetrické rozložení náboje uvnitř válce. Pro zdůvodnění může pomoci následující představa. Náboj je uvnitř válce rozložen symetricky, a proto nepoznáme žádný rozdíl, pokud válec libovolně natočíme kolem jeho osy. Pole kolem válce musí zůstat stále stejné, a proto i vektor intenzity musím mít v daném místě při různých otočeních stále stejný směr a velikost.
Gaussovou plochou zvolíme povrch válce, jehož osa splývá s osou nabitého válce. V tomto případě má vektor elektrické intenzity na celé ploše pláště válce stejnou velikost a je na ni kolmý. Naopak s podstavami válce je vektor intenzity rovnoběžný, proto je tok intenzity podstavami roven nule. Tím se nám zjednoduší výpočet celkového toku intenzity.
Počítáme-li intenzitu vně válce, bude mít Gaussův válec větší poloměr než nabitý válec. Uvnitř válce je tedy veškerý náboj rozložený v části válce o výšce h. Vyjádříme ho pomocí hustoty náboje a objemu nabitého válce.
Počítáme-li intenzitu uvnitř nabitého válce, bude Gaussův válec mít menší poloměr než nabitý válec. Pomocí hustoty náboje a objemu Gaussova válce vyjádříme náboj, který je uzavřen uvnitř Gaussova válce.
Potenciál vypočítáme z elektrické intenzity. Potenciál v daném místě se až na znaménko rovná integrálu intenzity z místa s nulovým potenciálem do tohoto místa. Nulový potenciál zvolíme na povrchu válce. (Podrobnější vysvětlení je uvedeno v nápovědě.)
Řešení: Intenzita vně válce
V tomto oddíle určíme intenzitu elektrického pole vně nabitého válce, tzn. pro z > R.
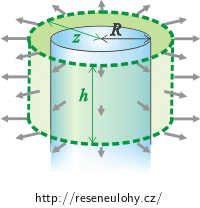
Využijeme Gaussovu větu:
\[\oint_\mathrm{S} \vec{E} \cdot \mathrm{d}\vec{S}\,=\, \frac{Q}{\varepsilon_0},\] \[\oint_\mathrm{S} \vec{E} \cdot \vec{n}\mathrm{d}S\,=\, \frac{Q}{\varepsilon_0}.\tag{*}\]Náboj je ve válci rozložen symetricky, proto je i elektrické pole vytvořené válcem symetrické. Vektor elektrické intenzity míří ve všech místech od osy válce (tj. je kolmý na plášť válce) a jeho velikost závisí pouze na vzdálenosti od osy válce.
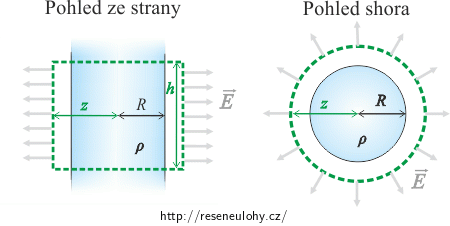
Jako Gaussovu plochu volíme povrch válce (na obrázcích vyznačen zeleně), jehož osa splývá s osou nabitého válce. Celkový tok intenzity plochou získáme sečtením toku podstavami a pláštěm válce.
Tok podstavami:Vektor elektrické intenzity je rovnoběžný s podstavami Gaussova válce a tok elektrické intenzity podstavami je tedy nulový. Celkový tok intenzity Gaussovou plochou je tedy roven pouze toku pláštěm válce.
Tok pláštěm:Vektor elektrické intenzity je kolmý k povrchu pláště válce, a proto platí \(\vec{E} \cdot \vec{n}\,=\,En\,=\,E\) (pozn. \(\vec{n}\) je jednotkový vektor).
S využitím těchto poznatků můžeme vyjádřit tok intenzity pláštěm a upravit integrál na levé straně Gaussovy věty:
\[\oint_\mathrm{pl} \vec{E} \cdot \vec{n}\mathrm{d}S\,=\,\oint_\mathrm{pl} E n\mathrm{d}S\,=\, \oint_\mathrm{pl} E\mathrm{d}S\,.\]Velikost vektoru elektrické intenzity E je ve všech místech pláště Gaussova válce stejná, a proto ji můžeme vyjmout před integrál jako konstantu. Dostáváme tedy vztah
\[\oint_\mathrm{pl} \vec{E} \cdot \vec{n}\mathrm{d}S\,=\,E \oint_\mathrm{pl} \mathrm{d}S\,=\,E S_\mathrm{pl},\]kde Spl = 2πzh je obsah pláště Gaussova válce (h je výška válce):
\[\oint_\mathrm{pl} \vec{E} \cdot \vec{n}\mathrm{d}S\,=\,E\, 2 \pi z h.\]Výsledný vztah dosadíme zpět do Gaussovy věty (*):
\[E 2 \pi z h\,=\, \frac{Q}{\varepsilon_0}.\]Vyjádříme velikost intenzity:
\[E \,=\, \frac{Q}{2 \pi \varepsilon_0 z h}.\tag{**}\]Zbývá vyjádřit náboj Q uvnitř zvolené Gaussovy plochy pomocí zadaných veličin.
Uvnitř plochy je část nabitého válce, náboj tedy můžeme vyjádřit pomocí jeho objemu V a objemové hustoty náboje ρ:
\[Q\,=\,V \varrho\,=\, \pi R^2 h \varrho.\]Dosadíme do vzorce (**) a upravíme:
\[E \,=\, \frac{\pi R^2 h \varrho}{2 \pi \varepsilon_0 z h}.\]Ve vzdálenosti z má elektrické pole nabitého válce intenzitu:
\[E \,=\, \frac{ R^2 \varrho}{2 \varepsilon_0}\,\frac{1}{ z }.\]Velikost intenzity E vně nabitého válce tedy lineárně klesá se vzdáleností z od osy válce.
Řešení: Intenzita uvnitř válce
V tomto oddíle určíme intenzitu elektrického pole uvnitř nabitého válce, tzn. pro z < R. Postup je podobný jako v předchozím oddíle Intenzita vně válce, proto není komentován tak podrobně.
Elektrickou intenzitu vypočítáme pomocí Gaussovy věty:
\[\oint_\mathrm{S} \vec{E} \cdot \mathrm{d}\vec{S}\,=\, \frac{Q_1}{\varepsilon_0},\]kde Q1 je náboj uvnitř zvolené Gaussovy plochy.
Za Gaussovu plochu zvolíme plášť válce, jehož osa je totožná s osou nabitého válce a má poloměr z < R.
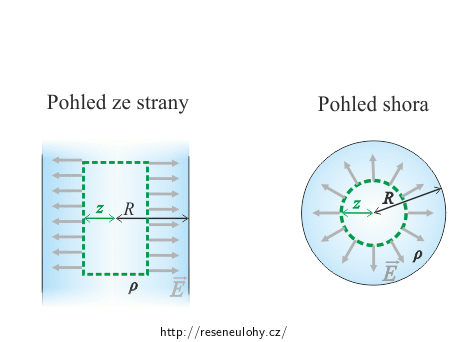
Tok intenzity podstavami válce je roven nule a celkový tok je tedy roven toku pláštěm válce.
Stejnými úvahami o symetrii jako v předchozím oddíle odvodíme, že vektor intenzity má na celé ploše pláště Gaussova válce stejnou velikost a je na něj kolmý, proto platí:
\[\oint_\mathrm{pl} \vec{E} \cdot \mathrm{d}\vec{S}\,=\,\oint_\mathrm{pl} En \mathrm{d}S\,=\,\oint_\mathrm{pl} E \mathrm{d}S\,=\,E\oint_\mathrm{pl} \mathrm{d}S\,=\,E\, 2 \pi z h\,.\]Výsledný vztah dosadíme zpět do Gaussovy věty (*):
\[E 2 \pi z h\,=\, \frac{Q_1}{\varepsilon_0}.\]Vyjádříme velikost intenzity:
\[E \,=\, \frac{Q_1}{2 \pi \varepsilon_0 z h}.\tag{+}\]Zbývá vyjádřit náboj Q1 uvnitř zvolené Gaussovy plochy pomocí zadaných veličin.
Protože Gaussův válec má menší poloměr než nabitý válec, je v něm uzavřena pouze část náboje. Náboj vyjádříme pomocí objemu Gausova válce V1 a objemové hustoty náboje ρ:
\[Q_1\,=\,V_1 \varrho\,=\, \pi z^2 h \varrho.\]Dosadíme do vzorce (+) a upravíme:
\[E \,=\, \frac{\pi z^2 h \varrho}{2 \pi \varepsilon_0 z h}.\]Ve vzdálenosti z má elektrické pole uvnitř nabitého válce intenzitu:
\[E \,=\, \frac{\varrho}{2 \varepsilon_0}\,z\,.\]Velikost intenzity E uvnitř nabitého válce tedy lineárně roste se vzdáleností z od osy válce.
Řešení: Potenciál vně válce
Potenciál v bodě A se až na znaménko rovná integrálu intenzity z místa s nulovým potenciálem do bodu A. Nulový potenciál zvolíme na povrchu válce pro R = 0 (podrobnější vysvětlení je uvedeno v nápovědě):
\[\varphi (z)\,=\, - \int_{R}^z \vec{E} \cdot \mathrm{d}\vec{z}.\]Pozn.: Pokud bychom volili nulový potenciál v nekonečnu jako u většiny úloh, nemohli bychom integrál dopočítat — podobně jako v úloze Pole rovnoměrně nabité roviny, viz její oddíl Potenciál.
Potenciál nezávisí na volbě integrační cesty, proto ji můžeme volit libovolně. V této úloze jako integrační cestu zvolíme část přímky, která směřuje kolmo na osu válce.
Vektor elektrické intenzity \(\vec{E}\) je rovnoběžný s vektorem \(\vec{z}\), proto můžeme integrál zjednodušit:
\[ \varphi (z)\,=\, - \int^\mathrm{z}_\mathrm{R} E \mathrm{d}z. \]Nyní musíme úlohu opět rozdělit na dva případy a spočítat zvlášť potenciál vně a uvnitř válce.
Nejprve vyjádříme potenciál ve vzdálenosti z vně válce:
\[\varphi (z)\,=\, - \int^\mathrm{z}_\mathrm{R} E \mathrm{d}z. \]Do integrálu dosadíme velikost intenzity, kterou jsme si vyjádřili v oddíle, a vytkneme před integrál všechny konstanty:
\[\varphi (z)\,=\, - \int^\mathrm{z}_\mathrm{R} \frac{\varrho R^2}{2 \varepsilon_0}\,\frac{1}{z}\, \mathrm{d}z \,=\, - \frac{\varrho R^2}{2 \varepsilon_0} \int^\mathrm{z}_\mathrm{R}\frac{1}{z}\, \mathrm{d}z.\]Vypočítáme určitý integrál:
\[\varphi (z)\,=\,- \,\frac{\varrho R^2}{2\varepsilon_0}\left[\ln z\right]^\mathrm{z}_{R}\,.\]Dosadíme meze integrálu a vytkneme konstanty:
\[\varphi (z)\,=\,-\frac{\varrho R^2}{2\varepsilon_0}\, \ln z\,+\,\frac{\varrho R^2}{2\varepsilon_0}\, \ln R\,=\,\frac{\varrho R^2}{2\varepsilon_0}\, \left(\ln R\,-\, \ln z\right)\,.\]Rozdíl logaritmů je logaritmus podílu:
\[\varphi (z)\,=\,\frac{\varrho R^2}{2\varepsilon_0}\, \ln \frac{R}{z}.\]Získali jsme velikost potenciálu vně válce ve vzdálenosti z.
Řešení: Potenciál uvnitř válce
Při výpočtu potenciálu uvnitř válce budeme postupovat podobně jako v předchozím oddíle. Potenciál vyjádříme ze vztahu:
\[ \varphi (z)\,=\, - \int^\mathrm{z}_\mathrm{R} \vec{E} \cdot \mathrm{d}\vec{z}\,=\, - \int^\mathrm{z}_\mathrm{R} E \mathrm{d}z \,.\]Dosadíme velikost intenzity uvnitř válce, kterou jsme si vyjádřili dříve, a dostaneme
\[\varphi (z)\,=\, - \int^\mathrm{z}_\mathrm{R} \frac{ \varrho}{2 \varepsilon_0}z\, \mathrm{d}z \,=\, - \,\frac{ \varrho}{2 \varepsilon_0}\int^\mathrm{z}_\mathrm{R} z\, \mathrm{d}z \,=\, - \,\frac{ \varrho}{2 \varepsilon_0}\left[\frac{z^2}{2} \right]^\mathrm{z}_\mathrm{R} \,.\]Dosadíme meze integrálu a po úpravě získáme potenciál uvnitř válce:
\[\varphi (z)\,=\,- \,\frac{ \varrho}{2 \varepsilon_0}\,\frac{z^2}{2} \, + \,\frac{ \varrho}{2 \varepsilon_0}\,\frac{R^2}{2} , \] \[\varphi (z)\,=\,- \,\frac{ \varrho}{4 \varepsilon_0}\,z^2 \, + \,\frac{ \varrho R^2}{4 \varepsilon_0},\] \[\varphi (z)\,=\,\frac{ \varrho}{4 \varepsilon_0} \,\left(R^2\,-\,z^2 \right).\]Odpověď
Vně válce platí pro intenzitu elektrického pole vztah
\[E \,=\, \frac{ R^2 \varrho}{2 \varepsilon_0}\,\frac{1}{ z }\,.\]Uvnitř válce platí pro intenzitu elektrického pole vztah
\[E \,=\, \frac{\varrho}{2 \varepsilon_0}\,z\,.\]V obou případech míří vektor elektrické intenzity od osy válce směrem ven (jestliže je náboj válce kladný).
Elektrický potenciál vně nabitého válce je dán vztahem
\[\varphi (z)\,=\,\frac{\varrho R^2}{2\varepsilon_0}\, \ln \frac{R}{z}\,.\]Elektrický potenciál uvnitř nabitého válce je dán vztahem
\[\varphi (z)\,=\,\frac{\varrho}{4 \varepsilon_0}\,\left(R^2\,-\,z^2 \right)\,.\]Grafy
Při kreslení grafů uvažujeme, že je válec nabitý kladným nábojem.
Graf závislosti velikosti el. intenzity na vzdálenosti od osy válce
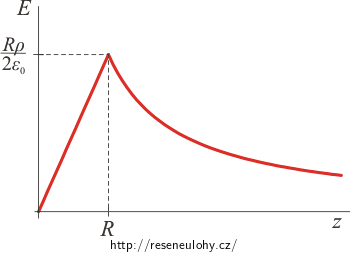
Uvnitř válce má intenzita elektrického pole velikost \(E \,=\, \frac{\varrho}{2 \varepsilon_0}\,z\,.\)
Vně válce má intenzita elektrického pole velikost \(E \,=\, \frac{ R^2 \varrho}{2 \varepsilon_0}\,\frac{1}{ z }\,.\)
První část grafu (pro hodnoty z od 0 do R) tvoří část přímky, která prochází počátkem. Pro vzdálenost z větší než R pak intenzita klesá (část grafu nepřímé úměrnosti, tj. část hyperboly).
Graf funkce je spojitý. Přesvědčíme se o tom, pokud do obou vztahů pro výpočet intenzity dosadíme z = R.
Pozn.: Intenzita elektrického pole je spojitá s výjimkou bodů, kdy prochází nabitou plochou. Při průchodu nabitou plochou zůstávají spojité pouze tečné složky vektoru. Normálové složky se mění „skokem“, který je úměrný plošné hustotě náboje. V této úloze ale žádné nabité plochy nejsou.
Graf závislosti el. potenciálu na vzdálenosti od osy válce
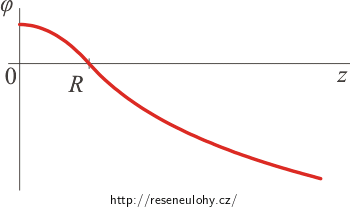
Elektrický potenciál uvnitř nabitého válce má velikost \(\varphi (z)\,=\,\frac{\varrho}{4 \varepsilon_0}\left(R^2\,-\,z^2 \right) \,.\)
Elektrický potenciál vně nabitého válce má velikost \(\varphi (z)\,=\,\frac{\varrho R^2}{2\varepsilon_0}\, \ln \frac{R}{z}\, .\)
První část grafu (pro hodnoty z od 0 do R) tvoří část paraboly s vrcholem na ose y . Pro větší vzdálenost intenzita klesá jako přirozený logaritmus.
Funkce je opět v bodě z = R spojitá a má navíc v tomto bodě spojité i první derivace a je tedy i hladká.
Pozn.: Elektrický potenciál je vždy spojitý, protože se jedná vlastně o práci při přenášení jednotkového náboje a ta se nemůže změnit „skokově“. Kromě bodů na nabitých plochách má potenciál spojité také první derivace, tj. je hladký.
Odkaz na podobnou úlohu



