RLC obvod s nastavitelnou kapacitou kondenzátoru
Úloha číslo: 739
Ke zdroji střídavého napětí o efektivní hodnotě 10 V a frekvenci 50 Hz jsou do série připojeny ideální cívka, rezistor o odporu 5 Ω a kondenzátor s proměnnou kapacitou. Při nastavení kapacity kondenzátoru na C1 = 100 μF teče obvodem stejný proud jako při nastavení kapacity na C2 = 200 μF. Určete indukčnost cívky a spočítejte efektivní hodnotu proudu, který teče obvodem při kapacitě C2.
Nápověda
Uvědomte si, co vyplývá z poznatku, že při různých kapacitách kondenzátoru protéká obvodem stále stejný proud. Jaká další veličina musí být pro obě nastavení kapacity kondenzátoru stejná?
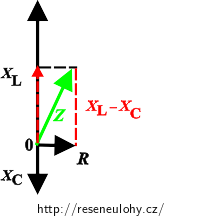
Nápověda – impedance sériového RLC obvodu
Připomeňte si, jaký je vztah pro celkovou impedanci sériového RLC obvodu a jak ho lze odvodit z diagramu pro impedance.
Rozbor
Teče-li při obou hodnotách kapacity kondenzátoru obvodem stejný proud, vyplývá z Ohmova zákona pro obvod se střídavým napětím, že v obou případech má obvod stejnou impedanci. Z tohoto poznatku vyjádříme indukčnost cívky zařazené v obvodu.
Při znalosti indukčnosti cívky jsme již snadno schopni spočítat proud tekoucí obvodem při dané kapacitě pomocí Ohmova zákona pro obvod se střídavým proudem.
Řešení
Platí-li, že proudy při obou hodnotách kapacity kondenzátoru jsou stejné, musí být stejné celkové impedance obvodu (podrobněji v nápovědě):
\[Z_1=Z_2. \]Pro impedance sériově zapojeného RLC obvodu můžeme psát:
\[\sqrt{R^2 + (X_\mathrm{L} - X_\mathrm{C1})^2}=\sqrt{R^2 + (X_\mathrm{L} - X_\mathrm{C2})^2},\]kde R je odpor rezistoru, XL induktance cívky a XC kapacitance kondenzátoru.
Dosadíme za induktanci a kapacitance:
\[\sqrt{R^2 + \left(\omega L - \frac{1}{\omega C_1}\right)^2}=\sqrt{R^2 + \left(\omega L - \frac{1}{\omega C_2}\right)^2},\]kde L je indukčnost cívky a ω je úhlová frekvence napětí zdroje.
Z této rovnosti postupně vyjádříme hledanou indukčnost cívky L. Nejprve obě strany rovnice umocníme:
\[R^2 + \left(\omega L - \frac{1}{\omega C_1}\right)^2=R^2 + \left(\omega L - \frac{1}{\omega C_2}\right)^2,\] \[ \left(\omega L - \frac{1}{\omega C_1}\right)^2= \left(\omega L - \frac{1}{\omega C_2}\right)^2.\]Nyní obě strany rovnice odmocníme:
\[ \omega L - \frac{1}{\omega C_1}= \pm \left(\omega L - \frac{1}{\omega C_2}\right).\]Odmocněním jsme dostali dvě možné rovnice:
\[ \omega L - \frac{1}{\omega C_1}= \omega L - \frac{1}{\omega C_2},\tag{1}\] \[ \omega L - \frac{1}{\omega C_1}= - \omega L + \frac{1}{\omega C_2}.\tag{2}\]Vezmeme-li první z rovnic a upravíme:
\[ \omega L - \frac{1}{\omega C_1}= \omega L - \frac{1}{\omega C_2}\quad\Rightarrow\quad \frac{1}{\omega C_1}= \frac{1}{\omega C_2}\quad\Rightarrow\quad C_1=C_2,\tag{1}\]je zřejmé, že tato rovnost nemůže nastat nikdy, protože je stálá frekvence zdroje.
Zůstává nám tedy druhá rovnice, ze které vyjádříme indukčnost cívky L:
\[ \omega L - \frac{1}{\omega C_1}= - \omega L + \frac{1}{\omega C_2},\tag{2}\] \[ 2\omega L = \frac{1}{\omega C_1} + \frac{1}{\omega C_2} = \frac{1}{\omega }\left(\frac{1}{C_1} + \frac{1}{ C_2}\right),\] \[ L = \frac{1}{2 {\omega}^2 }\left(\frac{1}{C_1} + \frac{1}{ C_2}\right) = \frac{1}{2 (2\pi f)^2 }\frac{C_1+C_2}{C_1 C_2} = \frac{1}{8(\pi f)^2 }\frac{C_1+C_2}{C_1 C_2},\]kde f je frekvence napětí zdroje.
Při znalosti indukčnosti cívky jsme již schopni spočítat proud tekoucí obvodem při dané kapacitě C2. Z Ohmova zákona bude platit:
\[ I = \frac{U}{Z_2},\]kde I je efektivní hodnota proudu a U efektivní hodnota napětí.
Nejdříve si vyjádříme velikost impedance Z2:
\[ Z_2 = \sqrt{R^2 + \left(\omega L - \frac{1}{\omega C_2}\right)^2}\]a dosadíme za indukčnost L, kterou jsme odvodili výše:
\[ L = \frac{1}{2 {\omega}^2 }\left(\frac{1}{C_1} + \frac{1}{ C_2}\right),\] \[ Z_2 = \sqrt{R^2 + \left(\frac{\omega}{2 {\omega}^2 }\left(\frac{1}{C_1} + \frac{1}{ C_2}\right) - \frac{1}{\omega C_2}\right)^2}.\]Upravíme:
\[ Z_2 = \sqrt{R^2 + \left(\frac{1}{2 {\omega} }\left(\frac{1}{C_1} + \frac{1}{ C_2}\right) - \frac{1}{\omega C_2}\right)^2}= \sqrt{R^2 + \left(\frac{1}{2 {\omega} C_1 }+\frac{1}{2 {\omega} C_2 } - \frac{1}{\omega C_2}\right)^2}= \] \[=\sqrt{R^2 + \left(\frac{1}{2 {\omega} C_1 }- \frac{1}{2\omega C_2}\right)^2}=\sqrt{R^2 + \left(\frac{C_2-C_1}{2 {\omega} C_1 C_2}\right)^2}=\sqrt{R^2 + \left(\frac{C_2-C_1}{4 \pi f C_1 C_2}\right)^2}.\]Dosadíme zpět do Ohmova zákona:
\[ I = \frac{U}{Z_2},\] \[ I =\frac{U}{\sqrt{R^2 + \left(\frac{C_2-C_1}{4 \pi f C_1 C_2}\right)^2}}.\]Zápis a číselné dosazení
U = 10 V efektivní hodnota napětí zdroje f = 50 Hz frekvence napětí zdroje R = 5 Ω odpor rezistoru C1 = 100 μF kapacita kondenzátoru C2 = 200 μF kapacita kondenzátoru L = ? (H) indukčnost cívky I = ? (A) efektivní hodnota proudu v obvodu při nastavení kapacity kondenzátoru C2
\[ L = \frac{1}{8(\pi f)^2 }\frac{C_1+C_2}{C_1 C_2}= \frac{1}{8(\pi\cdot 50)^2 }\frac{100{\cdot}10^{-6} +200{\cdot}10^{-6}}{100{\cdot}10^{-6} \cdot 200{\cdot}10^{-6} }\,\mathrm{H}\,\dot=\,0{,}76\,\mathrm H \]
\[ I =\frac{U}{\sqrt{R^2 + \left(\frac{C_2-C_1}{4 \pi f C_1 C_2}\right)^2}} =\frac{10}{\sqrt{5^2 + \left(\frac{200{\cdot}10^{-6}-100{\cdot}10^{-6}}{4\cdot \pi \cdot 50 {\cdot} 100\cdot10^{-6} \cdot 200{\cdot}10^{-6}}\right)^2}}\,\mathrm A\,\dot=\,1{,}06\,\mathrm A \]Odpověď
Indukčnost cívky je asi 0,076 H a obvodem teče při hodnotě kapacity 200 μF proud přibližně 1,06 A.