Nabitá půlobruč
Úloha číslo: 2008
Přímou integrací určete elektrickou intenzitu a potenciál na ose půlobruče o poloměru \(R\), která je homogenně nabita lineární hustotou \(\lambda\). Ověřte vztah mezi elektrickou intenzitou a potenciálem.
Pozn.: Osou půlobruče je myšlena osa pomyslné celé obruče.
Podobnost s úlohou o nabité obruči
Úloha o nabité půlobruči je velmi podobná úloze Nabitá obruč.
Nápověda – elektrická intenzita
Kladný bodový náboj Q vytváří ve vzdálenosti r pole o intenzitě
\[E=\frac{1}{4\pi\epsilon_0} \frac{Q}{r^2}.\]Vektor intenzity \(\vec{E}\) míří směrem od náboje, pokud je Q kladný. V opačném případě míří k náboji.
Zamyslete se nad tím, jak bychom tohoto poznatku mohli využít v této úloze.
Rozbor – elektrická intenzita
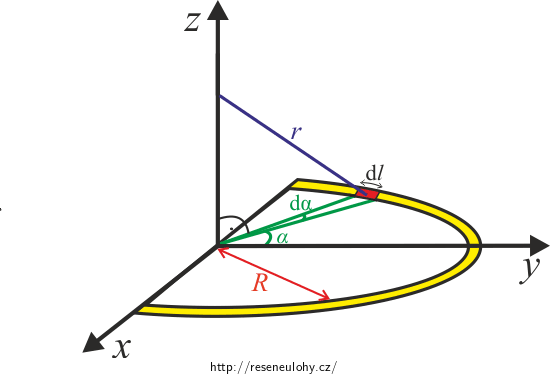
Nejprve si celou situaci nakreslíme do kartézských souřadnic. Osa půlobruče bude splývat
s osou z a půlobruč bude ležet v rovině xy. Do obrázku si vyznačíme také dvě z cylindrických
souřadnic \(\alpha\) a z. Cylindrickou souřadnici \(\rho\) nebudeme potřebovat, jelikož má půlobruč konstantní poloměr R.
Řešení – elektrická intenzita
Bodový náboj Q vytváří ve vzdálenosti r pole o velikosti intenzity
\[{E}=\frac{1}{4\pi\epsilon_0} \frac{Q}{r^2}.\]Je-li půlobruč nabita s lineární hustotou \(\lambda,\) potom má náboj na nekonečně malém kousku obruče dl velikost \[\textrm{d}Q = {\lambda} {\textrm{d}l},\]
kde \(\textrm{d}l=R\thinspace \textrm{d} \alpha\) (viz výpočet délky kruhového oblouku v radiánech).
Potom
\[\textrm{d}Q =\lambda R \thinspace \textrm{d}\alpha,\]a tudíž velikost intenzity od jednoho kousku obruče je
\[\textrm{d}E=\frac{1}{4\pi\epsilon_0} \frac{\textrm{d}Q}{r^2}=\frac{1}{4\pi\epsilon_0} \frac{\lambda R}{r^2}\textrm{d}\alpha.\tag{1}\]Nyní se zaměřme na směr intenzity. Bez újmy na obecnosti můžeme předpokládat, že půlobruč je nabitá kladně.
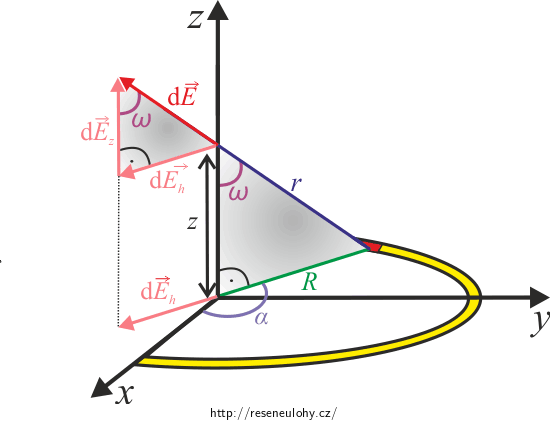
Z pravoúhlého trojúhelníku, který je vyznačen v obrázku, potom můžeme vyjádřit složku elektrické intenzity \(\textrm{d}E_\mathrm{z}\) pomocí funkce kosinus:
\[\textrm{d}E_\mathrm{z} = \textrm{d}E\cos\omega.\tag{2}\]Jelikož jsou pravoúhlé trojúhelníky vyznačené na obrázku podobné (podle věty uu), můžeme zapsat
\[\cos \omega = \frac{z}{r}.\]Z Pythagorovy věty víme
\[r^2 = z^2 + R^2, \tag{3}\]tudíž můžeme kosinus vyjádřit jako
\[\cos \omega= \frac{z}{\sqrt{z^2 + R^2}}.\tag{4}\]Spojením (1),(2),(3) a (4) dostaneme
\[\textrm{d}E_\mathrm{z} =\frac{1}{4\pi\epsilon_0} \frac{\lambda R z}{(z^2+R^2)^{3/2}}\textrm{d}\alpha, \]což zintegrujeme podél celého obvodu půlkružnice, tj. budeme integrovat přes úhel \(\alpha\):
\[ E_\mathrm{z} =\int_{0}^{\pi} \frac{1}{4\pi\epsilon_0} \frac{\lambda R z}{(z^2+R^2)^{3/2}}\textrm{d}\alpha. \]Vzdálenosti R a z nezávisí na úhlu \(\alpha\), proto je můžeme z integrálu vytknout:
\[ E_\mathrm{z} =\frac{1}{4\pi \epsilon_0} \frac{\lambda R z}{(z^2+R^2)^{3/2}} \int_{0}^{\pi} \textrm{d}\alpha. \]Po zintegrování dostáváme
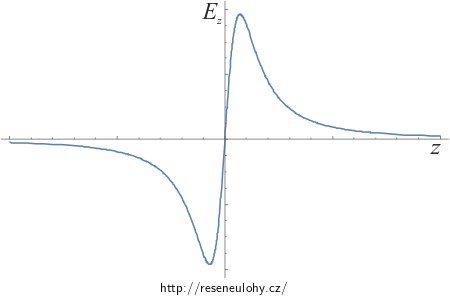
\[ E_\mathrm{z} =\frac{1}{4\epsilon_0} \frac{\lambda R z}{(z^2+R^2)^{3/2}}. \]Abychom mohli určit zbývající dvě složky elektrické intenzity, vyjádříme nejprve analogicky horizontální složku intenzity \(E_\mathrm{h}\).

Z pravoúhlého trojúhelníka je patrné, že
\[\textrm{d}E_\mathrm{h}=\textrm{d}E \sin\omega.\tag{5}\]Již víme, že jsou trojúhelníky podobné podle věty uu, můžeme proto vyjádřit sinus jako
\[\sin \omega = \frac {R} {r}.\]Přidáme-li poznatek z Pythagorovy věty (3), dostaneme
\[\sin \omega = \frac {R} {\sqrt{z^2 + R^2}}.\tag{6}\]Spojením (1),(3),(5) a (6) dostaneme
\[\textrm{d}E_\mathrm{h} =\frac{1}{4\pi\epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\textrm{d}\alpha. \]Nyní se zaměříme na vyjádření složek \(E_\mathrm{x}\) a \(E_\mathrm{y}\). Pro lepší názornost si celou situaci promítneme do roviny xy.
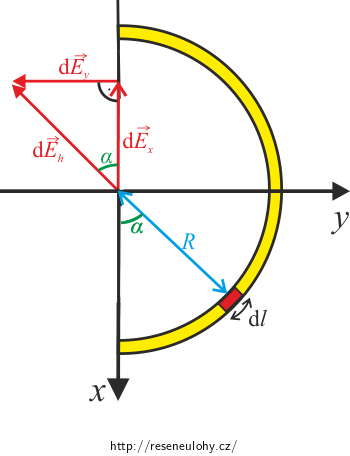
Z pravoúhlého trojúhelníka je zjevné, že
\[\textrm{d}E_\mathrm{y}=\textrm{d}E_h\sin \alpha,\] \[\textrm{d}E_\mathrm{x}=\textrm{d}E_h\cos \alpha.\]Začněme nejdříve s \(\textrm{d}E_\mathrm{y}:\)
\[\textrm{d}E_\mathrm{y}=\frac{1}{4\pi\epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\sin \alpha \thinspace\textrm{d}\alpha,\]což opět zintegrujeme podél celého obvodu půlkružnice, tj. budeme integrovat přes úhel \(\alpha\):
\[E_\mathrm{y}=\int_{0}^{\pi}\frac{1}{4\pi\epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\sin \alpha \thinspace\textrm{d}\alpha.\]Vzdálenosti R a z nezávisí na úhlu \(\alpha\), proto je můžeme z integrálu vytknout:
\[E_\mathrm{y}=\frac{1}{4\pi\epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\int_{0}^{\pi}\sin \alpha \thinspace\textrm{d}\alpha,\] \[E_\mathrm{y}=\frac{1}{4\pi\epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\left[-\cos \alpha \right]_{0}^{\pi},\]tedy
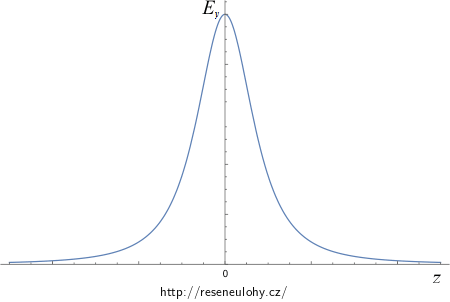
\[E_\mathrm{y}=\frac{1}{2\pi\epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}.\]Nyní vypočítáme \(\textrm{d}E_\mathrm{x}\):
\[\textrm{d}E_\mathrm{x}=\frac{1}{4\pi\epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\cos\alpha \thinspace\textrm{d}\alpha,\]což zintegrujeme podél celého obvodu půlkružnice, tj. budeme integrovat přes úhel \(\alpha\):
\[E_\mathrm{x}=\int_{0}^{\pi}\frac{1}{4\pi\epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\cos\alpha \thinspace\textrm{d}\alpha.\]Vzdálenosti R a z nezávisí na úhlu \(\alpha\), proto je můžeme z integrálu vytknout:
\[E_\mathrm{x}=\frac{1}{4\pi \epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\int_{0}^{\pi}\cos\alpha \thinspace\textrm{d}\alpha,\] \[E_\mathrm{x}=\frac{1}{4\pi \epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\left[\sin \alpha \right]_{0}^{\pi},\] \[E_\mathrm{x}=0,\]což nás vzhledem k symetrii půlkružnice nepřekvapuje.
Nápověda – potenciál
Analogicky jako při výpočtu elektrické intenzity využijeme vztahu pro potenciál bodového náboje. Potenciál bodového náboje ve vzdálenosti r je
\[φ = \frac{1}{4\pi\epsilon_0}\frac{Q}{r}.\]Vymyslete, jak vztahu využít pro výpočet potenciálu na ose půlobruče.
Řešení nápovědy
Půlobruč rozdělíme na malé kousky, které se budou chovat jako bodové náboje. Celkový potenciál získáme „sečtením“ (přesněji integrováním) všech příspěvků od těchto malých kousků.
Nejprve si celou situaci nakreslíme do kartézských souřadnic. Osa půlobruče bude splývat osou z a půlobruč bude ležet v rovině xy. Do obrázku si vyznačíme také dvě z cylindrických souřadnic \(\alpha\) a z. Cylindrickou souřadnici \(\rho\) nebudeme potřebovat, jelikož má půlobruč konstantní poloměr R.

Rozbor – potenciál
Nejprve si celou situaci nakreslíme do kartézských souřadnic. Osa půlobruče bude splývat
s osou z a půlobruč bude ležet v rovině xy. Do obrázku si vyznačíme také dvě z cylindrických
souřadnic \(\alpha\) a z. Cylindrickou souřadnici \(\rho\) nebudeme potřebovat, jelikož má půlobruč konstantní poloměr R.

Řešení – potenciál
Bodový náboj Q vytváří ve vzdálenosti r potenciál
\[\varphi= \frac{1}{4\pi\epsilon_0} \frac {Q} {r}.\]Zaměříme-li se na jednu malou část půlobruče, pak potenciál od této části v daném místě na ose půlobruče je
\[\textrm{d}\varphi= \frac{1}{4\pi\epsilon_0} \frac {\textrm{d}Q} {r}\tag{8}\]a jelikož je půlobruč nabita s lineární hustotou \(\lambda\), pak
\[\textrm{d}Q=\lambda\textrm{d}l.\]Využijeme-li navíc poznatku \(\textrm{d}l=R\thinspace\textrm{d}\alpha\), pak dostaneme
\[\textrm{d}Q=\lambda R\thinspace\textrm{d}\alpha.\tag{9}\] \[\textrm{d}\varphi=\frac{1}{4\pi \epsilon_0} \frac {\lambda R}{r}\textrm{d}\alpha. \tag{10}\]Nyní se zaměříme na vyjádření vzdálenosti r pomocí parametrů půlobruče a vzdálenosti z.
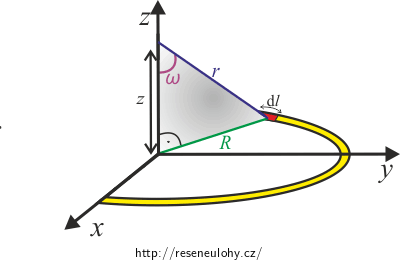
Z pravoúhlého trojúhelníka na obrázku můžeme z Pythagorovy věty vyjádřit
\[r = \sqrt{z^2 + R^2}.\tag{11}\]Spojíme-li (10) a (11) dostaneme
\[\textrm{d}\varphi=\frac{1}{4\pi\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}\textrm{d}\alpha, \]což zintegrujeme podél celého obvodu půlkružnice, tj. budeme integrovat přes úhel \(\alpha\):
\[\varphi=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\frac{1}{4\pi\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}\textrm{d}\alpha. \]Vzdálenosti R a z nezávisí na úhlu \(\alpha\), proto je můžeme z integrálu vytknout:
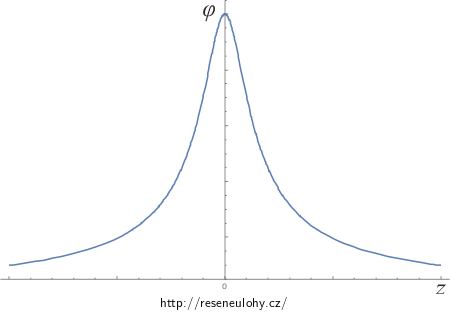
\[\varphi=\frac{1}{4\pi\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\textrm{d}\alpha, \] \[\varphi=\frac{1}{4\pi\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}\bigg[\alpha\bigg]_{-\frac{\pi}{2}}^{\frac{\pi}{2}}, \] \[\varphi=\frac{1}{4\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}. \]Pozn.: Potenciál na ose z nabité půlobruče je polovinou potenciálu nabité obruče (srovnání Nabitá obruč, Řešení c)). Tato vlastnost platí obecně, je to způsobeno tím, že potenciál je skalární funkce.
Nápověda – ověření vztahu
Potenciál a elektrickou intenzitu nám dává do vztahu jedna z rovností, ve které vystupuje matematický operátor gradient.
Zkuste si vzpomenout, popřípadě najít o jaký vztah se jedná. Připomeňte si, co gradient znamená a jak se počítá (v kartézských souřadnicích).
Řešení – ověření vztahu
Máme ověřit, zda platí vztah zmíněný v řešení nápovědy
\[\vec{E}=-\thinspace\text{grad}\thinspace\varphi.\]Ověření můžeme provést jen pro body na ose půlobruče a jen pro z–ovou složku, protože v části b) jsme určili pouze závislost potenciálu na souřadnici z.
Potenciál na ose půlobruče je
\[\varphi=\frac{1}{4\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}. \]Složka gradientu potenciálu do osy z je
\[\frac{\partial{\varphi}}{\partial{z}}=-\frac{1}{2} \frac {1} {\epsilon_0}\frac{\lambda R}{(z^2 + R^2)^{3/2}}2z = - \frac {1} {4\epsilon_0}\frac{\lambda R z}{{(z^2 + R^2)^{3/2}}},\]což dává z–ovou složku elektrické intenzity \(E_\mathrm{z}\) ve stejném tvaru jako přímý výpočet v části a):
\[E_\mathrm{z} =\frac {1} {4\epsilon_0}\frac{\lambda R z}{{(z^2 + R^2)^{3/2}}}.\]Nyní ještě ověříme, zda platí obrácený vztah
\[\varphi=-\int_\infty^{{\hat{z}}}{E_\mathrm{z}}\textrm{d}z,\]kde integrujeme podél osy \(z\) z „nekonečna“, kde je potenciál roven nule, do místa se souřadnicí \(\hat {z}\).
Dosadíme-li vypočítanou hodnotu \(E_\mathrm{z}\), dostaneme
\[\varphi=-\int_\infty^{{\hat{z}}} \ {\frac {1} {4\epsilon_0}\frac{\lambda R z}{{(z^2 + R^2)^{3/2}}}}\textrm{d}z,\] \[\varphi=-{\frac {\lambda R} {4\epsilon_0}\int_\infty^{{\hat{z}}}\frac{ z}{{(z^2 + R^2)^{3/2}}}}\textrm{d}z.\]Integrál budeme řešit pomocí substituce, použijeme substituci
\[R^2 + z^2 = a,\] \[2z \textrm{d}z = \textrm{d}a,\] \[z \rightarrow \infty \Rightarrow a \rightarrow \infty \qquad ; \qquad z = \hat{z} \Rightarrow a = \hat{z}^2 + R^2, \] \[\varphi=-{\frac {\lambda R} {8\epsilon_0}\int_\infty^{{\hat{z}^2 + R^2}}\frac{1 }{{a^{3/2}}}}\textrm{d}a,\] \[\varphi=\frac {\lambda R} {4\epsilon_0} \left[\frac{1}{a^{1/2}}\right]_\infty^{{\hat{z}^2 + R^2}}.\]Po dosazení mezí dostáváme
\[\varphi=\frac {\lambda R} {4\epsilon_0} \frac{1}{(R^2 + \hat{z}^2)^{1/2}} =\frac {1} {4\epsilon_0} \frac{\lambda R}{\sqrt{R^2 + \hat{z}^2}} .\]Jelikož \(\hat {z}\) je libovolný bod na ose z, můžeme přeznačit jeho souřadnici na \(z\):
\[\varphi=\frac {\lambda R} {4\epsilon_0} \frac{1}{(R^2 + {z}^2)^{1/2}} =\frac {1} {4\epsilon_0} \frac{\lambda R}{\sqrt{R^2 + {z}^2}},\]čímž dostaneme očekávaný výraz.
Odpověď
Elektrická intenzita na ose homogenně nabité půlobruče je \[ E_\mathrm{z} =\frac{1}{4\epsilon_0} \frac{\lambda R z}{(z^2+R^2)^{3/2}}, \] \[E_\mathrm{y}=\frac{1}{2\pi \epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}},\] \[E_\mathrm{x}=0.\] Potenciál na ose homogenně nabité půlobruče je \[\varphi=\frac{1}{4\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}. \]Dále jsme ověřili pro body na ose obruče platnost vztahu mezi \(\vec {E}\) a φ.
Grafy průběhu elektrické intenzity a potenciálu
Na následujících obrázcích si můžeme prohlédnout průběhy závislostí elektrické intenzity a potenciálu na vzdálenosti z od středu půlobruče.
Čtvrtkružnice a oblouk o úhlu β
Čtvrtkružnice
Výpočet elektrické intenzity a potenciálu na ose z jsme dělali pro půlkružnici. Ukažme si, jak by to dopadlo s čtvrtkružnicí.
Pro půlkružnici jsme odvodili následující vztahy:
\[ E_\mathrm{z} =\frac{1}{4\pi \epsilon_0} \frac{\lambda R z}{(z^2+R^2)^{3/2}} \int_{0}^{\pi} \textrm{d}\alpha, \] \[E_\mathrm{y}=\frac{1}{4\pi\epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\int_{0}^{\pi}\sin \alpha\thinspace\textrm{d}\alpha,\] \[E_\mathrm{x}=\frac{1}{4\pi \epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\int_{0}^{\pi}\cos \alpha\thinspace\textrm{d}\alpha.\]U čtvrtkružnice bude změna pouze v mezích integrálů:
\[ E_\mathrm{z} =\frac{1}{4\pi \epsilon_0} \frac{\lambda R z}{(z^2+R^2)^{3/2}} \int_{0}^{\frac{\pi}{2}} \textrm{d}\alpha, \] \[E_\mathrm{y}=\frac{1}{4\pi\epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\int_{0}^{\frac{\pi}{2}}\sin \alpha\thinspace\textrm{d}\alpha,\] \[E_\mathrm{x}=\frac{1}{4\pi \epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\int_{0}^{\frac{\pi}{2}}\cos \alpha\thinspace\textrm{d}\alpha.\]Po zintegrování dostaneme
\[ E_\mathrm{z} =\frac{1}{8 \epsilon_0} \frac{\lambda R z}{(z^2+R^2)^{3/2}}, \] \[E_\mathrm{y}=\frac{1}{4\pi\epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}},\] \[E_\mathrm{x}=\frac{1}{4\pi \epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}.\]Obdobně pro potenciál půlkružnice jsme odvodili
\[\varphi=\frac{1}{4\pi\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}\int_{0}^{\pi}\textrm{d}\alpha. \]U čtvrtkružnice bude změna pouze v mezích integrálu:
\[\varphi=\frac{1}{4\pi\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}\int_{0}^{\frac{\pi}{2}}\textrm{d}\alpha. \]Po zintegrování dostaneme
\[\varphi=\frac{1}{8\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}. \]Oblouk o úhlu \(\beta\)
Opět využijme výsledků, které jsme odvodili. Konkrétní úhel v mezích integrálů nyní nahradíme obecným úhlem \(\beta\):
\[ E_\mathrm{z} =\frac{1}{4\pi \epsilon_0} \frac{\lambda R z}{(z^2+R^2)^{3/2}} \int_{0}^{\beta} \textrm{d}\alpha, \] \[E_\mathrm{y}=\frac{1}{4\pi\epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\int_{0}^{\beta}\sin \alpha\thinspace\textrm{d}\alpha,\] \[E_\mathrm{x}=\frac{1}{4\pi \epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\int_{0}^{\beta}\cos \alpha\thinspace\textrm{d}\alpha,\] \[\varphi=\frac{1}{4\pi\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}\int_{0}^{\beta}\textrm{d}\alpha. \]Po zintegrování dostaneme
\[ E_\mathrm{z} =\frac{\beta}{4\pi \epsilon_0} \frac{\lambda R z}{(z^2+R^2)^{3/2}} , \] \[E_\mathrm{y}=\frac{1}{4\pi\epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}(-\cos\beta +1),\] \[E_\mathrm{x}=\frac{1}{4\pi \epsilon_0} \frac{\lambda R^2}{(z^2+R^2)^{3/2}}\sin\beta,\] \[\varphi=\frac{\beta}{4\pi\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}. \]Komentář – závislost na velikosti úhlu β
Srovnáme-li z složku elektrické intenzity půlkružnice, čtvrtkružnice a oblouku o úhlu \(\beta\), můžeme si všimnout, že je tato složka elektrické intenzity úměrná velikosti oblouku. V případě půlkružince je \(\beta =\pi\) a čtvrtkružnice \(\beta = \frac{\pi}{2}\).
Půlkružnice:
\[ E_\mathrm{z} =\frac{1}{4\epsilon_0} \frac{\lambda R z}{(z^2+R^2)^{3/2}}. \]Čtvrtkružnice:
\[ E_\mathrm{z} =\frac{1}{8 \epsilon_0} \frac{\lambda R z}{(z^2+R^2)^{3/2}}. \]Oblouk o úhlu \(\beta\):
\[ E_\mathrm{z} =\frac{\beta}{4\pi \epsilon_0} \frac{\lambda R z}{(z^2+R^2)^{3/2}}. \]Srovnáním potenciálů dojdeme ke stejnému závěru.
Půlkružnice:
\[\varphi=\frac{1}{4\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}. \]Čtvrtkružnice:
\[\varphi=\frac{1}{8\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}. \]Oblouk o úhlu \(\beta\):
\[\varphi=\frac{\beta}{4\pi\epsilon_0} \frac {\lambda R}{\sqrt{z^2 + R^2}}. \]U x a y složky elektrické intenzity úměrnost velikosti oblouku neplatí.
Potenciál a z složka elektrické intenzity jsou úměrné velikosti oblouku, který je nabit elektrickým nábojem, jelikož každý nabitý „kousíček“ obruče přispívá k celkové hodnotě stejně. Nicméně u x a y složky elektrické intenzity se příspěvek k celkové hodnotě mění, pro některé části obruče je kladný, pro některé naopak záporný, proto není možné, aby x a y složka elektrické intenzity byly úměrné velikosti oblouku.


