Sbírka řešených úloh

Rezonanční frekvence sériovo-paralelního zapojení

Úloha číslo: 792

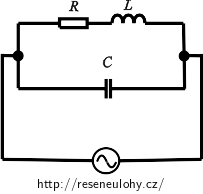
Určete rezonanční frekvenci obvodu zapojeného podle obrázku.

• Nápověda – obvod v rezonanci

  Uvědomte si, co platí pro obvod v rezonanci a jaký dopad to má na velikost komplexní impedance (admitance).

• Řešení nápovědy

  Je-li obvod v rezonanci, je fázový posun mezi napětím a proudem v obvodu nulový.

  Nulový fázový posun mezi napětím a proudem v obvodu se projeví na celkové komplexní impedanci i admitanci tím, že jejich imaginární složky budou nulové.

• Nápověda – paralelní obvod v rezonanci

  Uvědomte si, zda bude jednodušší vyjádřit celkovou impedanci či admitanci uvedeného obvodu.

• Řešení nápovědy

  Pro výpočet bude jednodušší vyjádřit si celkovou admitanci obvodu, protože ji získáme jako součet dílčích admitancí obou větví obvodu.

  Pozn.: Admitance je rovna převrácené hodnotě impedance.

• Rozbor

  Vyjádříme si celkovou admitanci jako součet převrácených hodnot impedancí pro jednotlivé větve. Rezonanční frekvence je taková, při které je proud a napětí v obvodu ve fázi. To znamená, že její hodnotu získáme z nulovosti imaginární složky celkové admitance.

• Řešení

  Při rezonanční frekvenci musí být napětí a proud obvodem ve fázi. To znamená, že imaginární složka komplexní admitance Y musí být nulová.

  Protože se jedná o paralelní zapojení větve, ve které je zapojen rezistor a cívka, a větve s kondenzátorem, získáme celkovou admitanci Y jako součet jednotlivých admitancí:

  \[ Y = Y_\mathrm{C} + Y_\mathrm{RL}, \]

  kde Y_C je admitance kondenzátoru a Y_RL admitance sériového zapojení cívky a rezistoru.

  ---

  Odvození velikosti admitance Y_RL:

  Nejdříve vyjádříme impedanci Z_RL větve, ve které je sériově zapojen rezistor a cívka, a admitanci Y_RL této větve určíme jako její převrácenou hodnotu:

  \[ Z_\mathrm{RL} = R + X_\mathrm{L}, \]

  kde R je odpor rezistoru a X_L induktance cívky. Dosadíme za induktanci X_L cívky:

  \[ Z_\mathrm{RL} = R + \mathrm{j} \omega L, \]

  kde ω je úhlová frekvence a L indukčnost cívky a j komplexní jednotka.

  Vyjádříme admitanci Y_RL této větve:

  \[ Y_\mathrm{RL} = \frac{1}{Z_\mathrm{RL}} = \frac{1}{R + \mathrm{j} \omega L}. \]

  Odvození velikosti admitance Y_C:

  Impedance Z_C větve, ve které je zapojen kondenzátor, je rovna kapacitanci kondenzátoru X_C s kapacitou o velikosti C:

  \[Z_\mathrm{C} = X_\mathrm{C} = \frac{1}{\mathrm{j} \omega C}. \]

  Pro admitanci lze psát:

  \[ Y_\mathrm{C} = \frac{1}{X_\mathrm{C}} = \frac{1}{\frac{1}{\mathrm{j} \omega C}}= \mathrm{j} \omega C. \]

  Do vztahu pro celkovou admitanci Y dosadíme vztahy odvozené výše:

  \[ Y = Y_\mathrm{C} + Y_\mathrm{RL}, \] \[ Y =\mathrm{j} \omega C + \frac{1}{R + \mathrm{j} \omega L}. \]

  ---

  Celkovou admitanci obvodu Y upravíme tak, abychom viděli její imaginární složku:

  \[ Y =\mathrm{j} \omega C + \frac{1}{R + \mathrm{j} \omega L} =\mathrm{j} \omega C + \frac{1}{R + \mathrm{j} \omega L} \,\frac{R - \mathrm{j} \omega L}{R - \mathrm{j} \omega L}=\mathrm{j} \omega C +\frac{R - \mathrm{j} \omega L}{R^2 + \omega^2 L^2}=\] \[=\mathrm{j} \omega C +\frac{R }{R^2 + \omega^2 L^2} - \frac{\mathrm{j} \omega L }{R^2 + \omega^2 L^2}=\frac{R }{R^2 + \omega^2 L^2} + \mathrm{j}\, \left(\omega C - \frac{ \omega L }{R^2 + \omega^2 L^2}\right). \]

  ---

  Při rezonanční frekvenci f platí, že imaginární složka celkové admitance Y je nulová, tedy platí:

  \[ \omega C - \frac{ \omega L }{R^2 + \omega^2 L^2} = 0.\]

  Vyjádříme úhlovou frekvenci zdroje napětí ω:

  \[ \omega C = \frac{ \omega L }{R^2 + \omega^2 L^2} ,\] \[ \omega C (R^2 + \omega^2 L^2) = \omega L ,\] \[ R^2 + \omega^2 L^2= \frac{L}{C} ,\] \[ \omega^2 L^2= \frac{L}{C}- R^2 ,\] \[ \omega = \sqrt{ \frac{1}{C L}- \frac{R^2}{ L^2} } .\]

  Dosadíme za úhlovou frekvenci ω = 2πf a vyjádříme frekvenci zdroje napětí f:

  \[ f= \frac{1}{2 \pi} \sqrt{ \frac{1}{C L}- \frac{R^2}{ L^2} } .\]

• Odpověď

  Rezonanční frekvence daného obvodu je dána vztahem:

  \[ f= \frac{1}{2 \pi} \sqrt{ \frac{1}{C L}- \frac{R^2}{ L^2} } .\]