Sbírka řešených úloh

Elektron a záporný iont

Úloha číslo: 761

• Zobecnění úlohy

  Záporně nabitý iont a elektron jsou dvě částice, které se liší svou hmotností a nábojem. Je tedy možné vypočítat obecně vzdálenost dopadu pro částici o hmotnosti m a náboji Q a až nakonec dosadit hodnoty pro elektron a záporný iont.

• Nápověda: Rychlost částice

  Při urychlování vykoná zdroj napětí práci, a tím dodá částici kinetickou energii. Vykonaná práce závisí na napětí zdroje a náboji částice.

• Nápověda: Pohyb částice

  

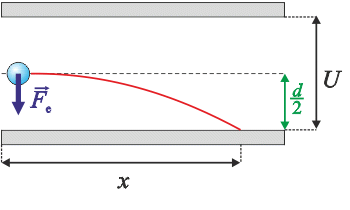
  Pohyb částice můžeme rozdělit na dvě složky: vodorovný a svislý pohyb.

  Ve vodorovném směru nepůsobí na částici žádná síla, proto je tento pohyb rovnoměrný.

  Ve svislém směru působí na částici síla elektrická, protože je tento pohyb rovnoměrně zrychlený. Zrychlení částice můžeme vyjádřit z druhého Newtonova zákona, do kterého dosadíme elektrickou sílu. Ta je přímo úměrná intenzitě elektrického pole a náboji elektronu.

• Rozbor

  Při urychlování elektronu vykoná zdroj napětí práci, a částice tak získá kinetickou energii. Z této energie můžeme zjistit rychlost, kterou částice vlétne mezi desky kondenzátoru.

  Poté, co vlétne částice mezi desky kondenzátoru, začne na něj kolmo na směr pohybu působit elektrická síla.

  Pohyb částice můžeme rozdělit na dvě části:

  1. Rovnoměrný pohyb ve vodorovném směru rychlostí, kterou částice vlétla mezi desky.
  2. Rovnoměrně zrychlený pohyb ve svislém směru způsobený elektrickou silou.

  Jakou dráhu částice uletí, zjistíme z vodorovného rovnoměrného pohybu.

  Ve vztahu pro dráhu vystupuje čas, který vyjádříme ze zrychleného pohybu ve svislém směru. Zrychlení částice vyjádříme pomocí elektrické síly a druhého Newtonova zákona.

• Řešení: Výpočet rychlosti a zrychlení

  Výpočet rychlosti částice

  Práce vykonaná při urychlování částice musí být stejná jako kinetická energie, kterou částice získala (podrobnější postup výpočtu naleznete v úloze Elektron v obrazovce osciloskopu v části Rychlost, kterou elektron vlétne mezi desky):

  \[W\,=\,E_\mathrm{k},\] \[QU_0\,=\,\frac{1}{2}mv^2,\] \[v\,=\,\sqrt{\frac{2QU_0}{m}}.\tag{1}\]

  Výpočet času dopadu částice na desku

  

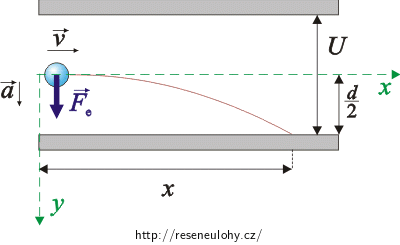
  Po vlétnutí mezi desky kondenzátoru začne na částici působit elektrická síla, jenž způsobí, že se začne pohybovat ve směru osy y rovnoměrně zrychleně.

  Pro vzdálenost \(\frac{d}{2}\), kterou částice urazí, než dopadne na desku, musí platit vztah:

  \[\frac{d}{2}\,=\,\frac{1}{2}at_\mathrm{d}^2\,.\]

  Vyjádříme čas dopadu částice na desku t_d:

  \[d\,=\,a t_\mathrm{d}^2,\] \[t_\mathrm{d}\,=\,\sqrt{\frac{d}{a}}.\tag{*}\]

  Zrychlení částice způsobuje elektrická síla. Toto zrychlení můžeme vypočítat z druhého Newtonova zákona (podrobnější postup výpočtu zrychlení naleznete opět v úloze Elektron v obrazovce osciloskopu v části Zrychlení elektronu ve svislém směru):

  \[a\,=\,\frac{F_\mathrm{e}}{m}.\]

  Elektrickou sílu můžeme vyjádřit pomocí intenzity elektrického pole a náboje částice F_e = QE:

  \[a\,=\,\frac{QE}{m}.\]

  Toto zrychlení dosadíme do vzorce (*) pro výpočet času dopadu:

  \[t_\mathrm{d}\,=\,\sqrt{\frac{d}{\frac{QE}{m}}},\] \[t_\mathrm{d}\,=\,\sqrt{\frac{dm}{QE}}.\tag{2}\]

• Řešení: Výpočet uražené vzdálenosti

  Ve směru osy x nepůsobí na částici žádná síla. Částice se tedy pohybuje rovnoměrně, a proto bude pro vzdálenost uraženou do dopadu:

  \[x\,=\,v t_\mathrm{d}\,.\]

  Rychlost a zrychlení jsme vypočítali v samostatném oddílu. Nyní tedy dosadíme vyjádřené vztahy (1) a (2):

  \[x\,=\,\sqrt{\frac{2QU_0}{m}} \sqrt{\frac{dm}{EQ}}\,,\] \[x\,=\,\sqrt{\frac{2d U_0}{E}}.\]

  Dosadíme za napětí vztah \(E\,=\,\frac{U}{d}\):

  \[x\,=\,\sqrt{\frac{2d^2 U_0}{U}}.\]

  Vidíme, že vzdálenost uražená do dopadu nezávisí na hmotnosti ani na náboji částice, a proto dopadnou iont i elektron do stejné vzdálenosti. Tento výsledek je dán tím, že uvažujeme stejné urychlující napětí, pokud by např. obě částice vlétly mezi desky kondenzátoru se stejnou rychlostí, potom by uražená vzdálenost byla rozdílná.

• Odpověď

  Elektron i iont dopadnou na stejné místo, protože uražená vzdálenost nezávisí na hmotnosti ani na náboji částice.

• Jednodušší úloha

  Vhodné je nejdříve vyřešit podobnou úlohu Elektron v obrazovce osciloskopu, která má podrobnější komentář k řešení.