Sbírka řešených úloh

Rovnováha tří nábojů

Úloha číslo: 36

• Nápověda: Jak začít

  Nakreslete si síly, které na náboj Q₃ působí.

  Jaká je výsledná síla působící na náboj Q₃ v místě, kde se ustálí?

• Nápověda: Coulombův zákon

  Elektrická síla závisí přímo úměrně na velikosti obou nábojů a nepřímo úměrně na kvadrátu jejich vzdálenosti.

• Obrázek sil působících na náboj Q₃

  

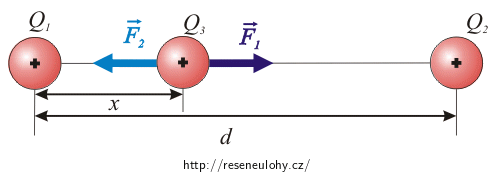
  Síly působící na náboj Q₃ jsou odpudivé. Náboj Q₁ působí silou \(\vec{F_1}\) a náboj Q₂ silou \(\vec{F_2}\). Prohlédněte si obrázek.

• Rozbor

  Třetí náboj se ustálí v místě, kde je výslednice všech působících sil nulová.

  První a druhý náboj působí na náboj Q₃ odpudivou elektrickou silou. Výslednice těchto dvou sil má být rovna nule, proto musí mít síly opačný směr a stejnou velikost.

  Podle Coulombova zákona závisí velikost elektrické síly přímo úměrně na velikosti obou nábojů a nepřímo úměrně na kvadrátu jejich vzdálenosti.

  Porovnáním velikostí obou sil získáme podmínku pro vzdálenost náboje Q₃ od náboje Q₁.

• Řešení: Úvahou

  Náboj Q₃ se ustálí v místě, kde výslednice elektrických sil od nábojů Q₁ a Q₂ bude nulová. Všechny náboje se navzájem odpuzují, takže síly od prvního a druhého náboje mají opačný směr (viz obrázek). Aby byla výslednice nulová, musí mít obě síly stejnou velikost.

  Velikost elektrické síly je přímo úměrná velikosti obou nábojů a nepřímo úměrná kvadrátu vzdálenosti.

  Náboje Q₁ a Q₂ jsou stejně velké. Rozdíl ve velikosti obou elektrických sil může být dán pouze vzdáleností náboje Q₃ od nábojů Q₁ a Q₂ . Jediné místo, kde je tato vzdálenost od obou nábojů stejná, je přesně uprostřed mezi těmito náboji. Třetí náboj se tedy ustálí zde.

• Řešení: Výpočet, kde se náboj ustálí

  Protože náboje Q₁ a Q₃ mají stejné znaménko, odpuzují se elektrickou silou, označíme si ji \(\vec{F_1}\). Také náboje Q₂ a Q₃ se odpuzují silou, tuto sílu si označíme \(\vec{F_2}\).

  Velikost obou sil spočítáme z Coulombova zákona:

  \[F_1=k\frac{Q_1Q_3}{x^2},\] \[F_2=k\frac{Q_2Q_3}{\left(d-x\right)^2}.\]

  V místě, kde se náboj Q₃ ustálí, musí být výslednice těchto dvou sil nulová. Z toho vyplývá, že síly \(\vec{F_1} \) a\( \vec{F_2}\) mají v tomto místě opačný směr (to je splněno — viz obrázek) a jsou stejně velké:

  \[F_1=F_2.\]

  Za obě síly dosadíme jejich vyjádření pomocí Coulombova zákona:

  \[k\frac{Q_1Q_3}{x^2}=k\frac{Q_2Q_3}{\left(d-x\right)^2}\]

  a zkrátíme k a Q₃:

  \[\frac{Q_1}{x^2}=\frac{Q_2}{\left(d-x\right)^2}\hspace{20px}|\,\cdot x^2{\left(d-x\right)^2},\] \[Q_1\left(d-x\right)^2=Q_2x^2.\]

  Z tohoto vztahu bychom mohli spočítat polohu třetího náboje, pro jakkoli velké náboje Q₁ a Q₂.

  Naše náboje Q₁ a Q₂ mají stejnou velikost, takže je můžeme také zkrátit:

  \[x^2=\left(d-x\right)^2.\]

  Rovnici budeme postupně upravovat. Umocníme závorku, odečteme stejné členy a poté vyjádříme neznámou vzdálenost x:

  \[x^2=d^2 - 2dx + x^2,\] \[0=d^2 - 2dx, \] \[2dx=d^2 \hspace{20px}|\,:\,d, \] \[2x = d, \] \[x=\frac{d}{2}.\]

  Vidíme, že třetí náboj se ustálí uprostřed.

• Nápověda: Stabilní a labilní rovnováha

  Jestliže náboj vychýlíme z rovnovážné polohy a výslednice působících sil vrací náboj zpět do původní polohy, je rovnováha stabilní.

  Naopak jestliže po vychýlení výsledná síla „táhne“ náboj stále dále od rovnovážné polohy, je rovnováha labilní.

• Řešení: Bude rovnováha stabilní nebo labilní?

  Posuneme-li třetí náboj ze středu na jednu stranu, změní se velikost sil, které na něj působí.

  Odpudivá elektrická síla od náboje, který je blíže, se zvětší. Naopak od náboje, který je vzdálenější, bude odpudivá síla menší.

  

  

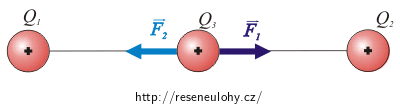
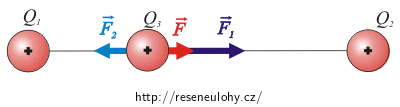
  Na obrázku vidíme, že výsledná síla bude směřovat zpět do středu. Vychýlíme-li náboj na druhou stranu, bude výsledná síla opět směřovat do středu.

  Tato rovnovážná poloha je tedy stabilní.

• Odpověď

  Náboj Q₃ se ustálí uprostřed mezi náboji Q₁ a Q₂.

  Rovnovážná poloha je stabilní.

• Co by se změnilo, pokud by třetí náboj měl opačné znaménko.

  Pokud by měl náboj Q₃ opačné znaménko, měly by síly působící na něj pouze opačný směr. Velikost sil by byla stále stejná. Náboj Q₃ by se proto ustálil opět uprostřed.

  

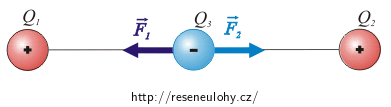
  Rovnováha by ale byla labilní, protože při jakémkoli vychýlení náboje ze středu by výsledná síla směřovala od středu ven.

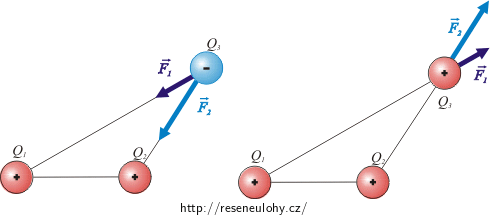
• Mohl by být náboj Q₃ v rovnováze i někde jinde?

  Třetí náboj nemůže být v rovnováze jinde než na úsečce spojující první dva náboje, protože nikdy nedostaneme nulovou výslednici sil od obou nábojů. Prohlédněte si následující obrázky.

  

  

  

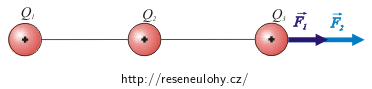
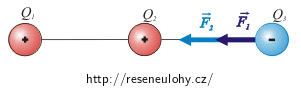
• Dynamický prvek

  Následující aplet zobrazuje tři náboje v rovině, dva jsou umístěny pevně a s jedním je možné hýbat (pomocí myši). Všechny tři náboje jsou kladné a jejich velikosti lze nastavit pomocí posuvníků (myší nebo lze využít šipky na klávesnici).

  Aplet zobrazuje elektrické síly působící na pohyblivý náboj od prvního a druhého náboje (černou barvou) a jejich výslednici (červeně).

  Úkoly pro práci s apletem

  1. Rozhodněte, zda může být výslednice sil nulová někde mimo přímku spojující nepohyblivé náboje 1 a 2.

  2. Nejprve rozmyslete a pak si svoji doměnku ověřte pomocí apletu: Jak ovlivní směr výslednice sil změna velikosti pohyblivého náboje? Platí totéž i pro změnu velikosti nepohyblivého náboje?

  3. Nastavte velikosti nábojů \(q_1 = 5, \space q_2 = 5,\space q = 5.\) Rozmyslete si, ve kterém bodě bude výsledná síla působící na pohyblivý náboj nulová. Změní se tento bod, pokud změním velikost náboje \(q\)? Svoje úvahy ověřte pomocí apletu.

  4. Nastavte velikosti nábojů \(q_1 = 2, \space q_2 = 8,\space q = 10.\) Rozmyslete, jaký bude poměr vzdáleností nábojů \(\frac{|d_\mathrm{q_1q}|}{|d_\mathrm{q_2q|}}\) v místě, kde je výsledná síla nulová. Svoje úvahy ověřte pomocí apletu.

  5. Nastavte velikosti nábojů \(q_1 = 5, \space q_2 = 5,\space q = 10.\) Nalezněte alespoň tři body, kde výslednice směřuje svisle. Nalezněte všechny body, kde výslednice směřuje svisle. Vyzkoušejte, jak se situace změní, pokud \(q_1\) a \(q_2\) nastavíte na různé hodnoty.

  6. Nastavte velikosti nábojů \(q_1 = 5, \space q_2 = 5,\space q = 10.\) Nalezněte alespoň tři body, kde výslednice směřuje vodorovně. Nalezněte všechny body, kde výslednice směřuje vodorovně. Vyzkoušejte, jak se situace změní, pokud \(q_1\) a \(q_2\) nastavíte na různé hodnoty.