Spojování kondenzátorů I
Úloha číslo: 2014
Kondenzátory jsou zapojeny dle obrázku. Určete celkovou kapacitu zapojení, napětí a náboje na deskách jednotlivých kondenzátorů při zapojení na napětí 100 V.
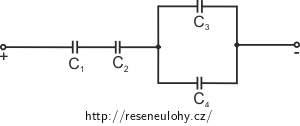
Nejprve počítejte obecně, poté pro hodnoty \(C_1 = C_3 = 1\ µ\mathrm{F},\ C_2 = C_4 = 10\ µ \mathrm{F}\).
Nápověda – kapacita, napětí a náboj
Kapacita vyjadřuje schopnost vodiče uchovat elektrický náboj. Pro daný kondenzátor (vodič) je konstantní a je definována jako
\[C = \frac {Q}{U},\]kde Q je náboj na kondenzátoru při napětí U. Více o kapacitě si můžete přečíst na Encyklopedie fyziky
.
Vyhledejte si vztahy týkající se kapacity, napětí a náboje pro sériově a paralelně zapojené kondenzátory.
Rozbor
Paralelně zapojené kondenzátory můžeme nahradit jedním kondenzátorem s kapacitou, která je rovna součtu kapacit na obou kondenzátorech. Tím získáme obvod jen se třemi sériově zapojenými kondenzátory. Při sériovém zapojení je převrácená hodnota celkové kapacity rovna součtu převrácených hodnot kapacit jednotlivých kondenzátorů. Tak určíme celkovou kapacitu.
Celkový náboj je přímo úměrný celkové kapacitě a celkovému napětí (tj. napětí na baterii).
Známe-li napětí a celkovou kapacitu zapojení, můžeme dopočítat celkový náboj. Náboje na kondenzátorech 1,2 a kondenzátoru 34 jsou rovny celkovému náboji. Ze znalosti náboje a kapacity kondenzátoru můžeme dopočítat napětí. Napětí na kondenzátorech 3 a 4 je rovno napětí na kondenzátoru 34, ze znalosti kapacity a napětí dopočítáme náboj.

Řešení – kapacita

Pro vypočítání celkové kapacity využijeme poznatků z nápovědy. Zaměříme se nejprve na paralelní část obvodu a kondenzátory \( C_3,\ C_4\) nahradíme kondenzátorem \(C_{34} \) (dle vztahu z nápovědy).
\[C_{34} = C_3 + C_4,\] \[C_{34} = 1\ µF + 10\ µF = 11 \ µF.\]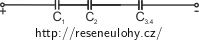
U sériové části postupujeme analogicky. Kondenzátory \( C_1,\ C_2, \ C_{34}\) nahradíme kondenzátorem \(C_\mathrm{C}\).
Pro celkovou kapacitu platí
\[\frac{1}{C_{C}} = \frac {1}{C_1} + \frac{1}{C_2} + \frac{1}{C_{34}},\] \[\frac{1}{C_{C}} = \frac {1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3 + C_4},\] \[\frac {1}{C_{C}} = \frac {(C_3 + C_4)C_2 + (C_3+C_4)C_1 + C_1C_2}{C_1C_2(C_3+C_4)}.\]Což po úpravě dává obecné řešení:
\[{C_\mathrm{C}} = \frac {C_1C_2(C_3+C_4)}{(C_3 + C_4)C_2 + (C_3+C_4)C_1 + C_1C_2}.\]Využijeme-li toho, že v této úloze speciálně platí \(C_1 = C_3 \) a \(C_2 = C_4, \) získáme
\[{C_\mathrm{C}} = \frac {C_1C_2(C_1+C_2)}{(C_1 + C_2)C_2 + (C_1+C_2)C_1 + C_1C_2}.\]Vytkneme výraz \(C_1 + C_2\):
\[{C_\mathrm{C}} = \frac {C_1C_2(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2}.\]Dosadíme zadané hodnoty:
\[{C_\mathrm{C}} = \frac {1 {\cdot} 10\cdot(1+10)}{(1 + 10)^2 + 1 {\cdot} 10}\, µF,\] \[C_\mathrm{C} \doteq 0{,}84\ µF.\]Řešení – napětí a náboj
V předchozím oddíle jsme spočetli celkovou kapacitu zapojení \(C_\mathrm{C} = \frac {C_1C_2(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2} \doteq 0{,}84 \ µF\).
Z definice kapacity \(C = \frac {Q} {U}\) spočítáme celkový náboj:
\[Q_\mathrm{C}= C_C U,\] \[Q_\mathrm{C} = \frac {C_1C_2(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2} U.\]Náboj na kondenzátorech \(C_1, C_2 \) a \( C_{34}\) je stejný a je roven celkovému náboji \(Q_\mathrm{C}\):
\[Q_\mathrm{C} = Q_1 = Q_2 = Q_{34}.\]Z definice kapacity dopočteme napětí na jednotlivých kondenzátorech.
Kondenzátor \(C_1\)
\[U_1 = \frac {Q_1}{C_1} = \frac {\frac {C_1C_2(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2}U}{C_1} = \frac {C_2(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2}U\]Kondenzátor \(C_2\)
\[U_2 = \frac {Q_2}{C_2}= \frac {\frac {C_1C_2(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2}U}{C_2} = \frac {C_1(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2}U\]Kondenzátor \(C_{34}\)
\[U_{34} = \frac {Q_{34}}{C_{34}}\]Z předchozích výpočtů víme, že \(C_\mathrm{34} = C_3 + C_4 = C_1 + C_2\),
\[U_{34} = \frac {\frac {C_1C_2(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2}U}{C_1 + C_2} = \frac {C_1C_2}{(C_1 + C_2)^2 + C_1C_2}U.\]Ověřme ještě naše výpočty. Mělo by platit \(U = U_1 + U_2 + U_{34}\):
\[Lev\acute{a}\ strana= U,\] \[Prav\acute{a}\ strana= U_1 + U_2 + U_{34} =\frac {C_2(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2}U + \frac {C_1(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2}U+\frac {C_1C_2}{(C_1 + C_2)^2 + C_1C_2}U = \] \[=U \frac {C_2(C_1 +C_2) + C_1(C_1+C_2) + C_1C_2}{(C_1 + C_2)^2 + C_1C_2} = U \frac {(C_1 + C_2)^2 + C_1C_2}{(C_1 + C_2)^2 + C_1C_2} = U, \] \[Lev\acute{a}\ strana = Prav\acute{a}\ strana.\]Kondenzátory \(C_{3}\) a \(C_{4}\)
Napětí na paralelně spojených kondenzátorech je stejné, v našem případě
\[U_3 = U_4 = U_{34}.\]Z definice kapacity dopočítáme náboj:
\[Q_3 = U_3 C_3= \frac {C_1C_2}{(C_1 + C_2)^2 + C_1C_2}U C_1 = \frac {C_1^2C_2}{(C_1 + C_2)^2 + C_1C_2}U,\] \[Q_4 = U_4 C_4 = \frac {C_1C_2}{(C_1 + C_2)^2 + C_1C_2}U C_2 = \frac {C_1C_2^2}{(C_1 + C_2)^2 + C_1C_2}U.\]Ověřmě naše výpočty. Mělo by platit \(Q_3 + Q_4 = Q_{34} = Q_C\):
\[Lev\acute{a}\ strana = Q_3 + Q_4 = \frac {C_1^2C_2}{(C_1 + C_2)^2 + C_1C_2}U + \frac {C_1C_2^2}{(C_1 + C_2)^2 + C_1C_2}U =\frac {C_1^2C_2 +C_1C_2^2 }{(C_1 + C_2)^2 + C_1C_2}U= \] \[=\frac {C_1C_2(C_1 + C_2)}{(C_1 + C_2)^2 + C_1C_2}U, \] \[Prav\acute{a}\ strana = Q_{34}=Q_\mathrm{C} = \frac {C_1C_2(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2} U, \] \[Lev\acute{a}\ strana = Prav\acute{a}\ strana.\]Dosazení konkrétních hodnot
\(C_1 = C_3 = 1\ \mu\textrm{F},\ C_2 = C_4 = 10\ \mu\textrm{F},\ U = 100 \textrm{V}. \)
\[Q_\mathrm{C} = Q_1 = Q_2=\frac {C_1C_2(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2} U =\frac {1 {\cdot} 10\cdot(1+10)}{(1 + 10)^2 + 1{\cdot}10}100\ \mu\textrm{C} \doteq 84\ \mu \textrm{C}.\] \[U_1 = \frac {C_2(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2}U = \frac {10\cdot(1+10)}{(1 + 10)^2 + 1{\cdot}10}\cdot100\ \textrm{V} \doteq 84\ \textrm{V}.\] \[U_2 = \frac {C_1(C_1+C_2)}{(C_1 + C_2)^2 + C_1C_2}U = \frac {1\cdot(1+10)}{(1 + 10)^2 + 1{\cdot}10}\cdot100\ \textrm{V} \doteq 8{,}4\ \textrm{V}.\] \[U_{34} =U_3=U_4 = \frac {C_1C_2}{(C_1 + C_2)^2 + C_1C_2}U = \frac {1 {\cdot} 10}{(1 + 10)^2 + 1{\cdot} 10}\cdot100\ \textrm{V} \doteq 7{,}6\ \textrm{V}. \] \[Q_3 = \frac {C_1^2C_2}{(C_1 + C_2)^2 + C_1C_2}U = \frac {1^2{\cdot}10}{(1 + 10)^2 + 1{\cdot} 10}\cdot100\ \mu\textrm{C} \doteq 7{,}6 \ \mu\textrm{C}.\] \[Q_4 = \frac {C_1C_2^2}{(C_1 + C_2)^2 + C_1C_2}U = \frac {1 {\cdot} 10^2}{(1 + 10)^2 + 1{\cdot}10}\cdot100\ \mu\textrm{C} \doteq 76 \ \mu\textrm{C}.\]Odpověď
Celková kapacita zapojení \(C = 0{,}84\ µF.\)
Náboje a napětí na jednotlivých kondenzátorech:
\[Q_1 = 84\ \mu \textrm{C} \quad U_1 = 84\ V \qquad C_1 = 1 \ \mu\textrm{F}\] \[Q_2 = 84\ \mu \textrm{C} \qquad U_2 = 8{,}4\ V \qquad C_2 = 10 \ \mu\textrm{F}\] \[Q_3 = 7{,}6\ \mu \textrm{C} \qquad U_3 = 7{,}6\ V \qquad C_3 = 1 \ \mu\textrm{F}\] \[Q_4 = 76\ \mu \textrm{C} \qquad U_4 = 7{,}6\ V \qquad C_4 = 10 \ \mu\textrm{F}\]Komentář – výsledky
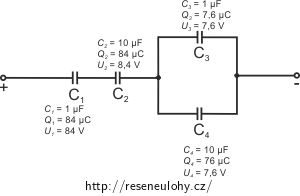
Kapacita kondenzátoru 4 je desetkrát větší než kapacita kondenzátoru 3. Srovnáme-li náboje, vidíme, že se náboj rozdělil v poměru kapacit (náboj na 4 je desetkrát větší než na 3). Obdobně kondenzátor 2 má desetkrát větší kapacitu než kondenzátor 1. Srovnáme-li napětí, vidíme, že se rozdělilo v opačném poměru kapacit (napětí na 2 je desetkrát menší než na 1).
Dynamický prvek − paralelní zapojení
Úlohy pro práci s apletem
- Měňte celkové napětí v obvodu. Pozorujte a popište, jak se mění napětí a náboj na obou kondenzátorech (v pravé části jsou číselné hodnoty i jejich grafické znázornění).
- Nastavujte různé hodnoty kapacit obou kondenzátorů a pozorujte, zda a případně jak se na nich mění napětí.
- Nastavujte různé hodnoty kapacit obou kondenzátorů a pozorujte, jak se mění celková kapacita zapojení (číselná hodnota celkové kapacity je v levé části). Jaký vztah platí pro celkovou kapacitu?
- Pokračujte v předchozím úkolu a ověřte, zda pro celkový náboj platí vztah \(Q=Q_1 + Q_2.\)
- Nastavte kapacity kondenzátorů tak, aby byly v poměru 1:2, a pozorujte, v jakém poměru jsou náboje a napětí na kondenzátorech. Nastavte i další jednoduché poměry kapacit. Na základě svých pozorování zformulujte závěry o tom, jak souvisí poměr kapacit s hodnotami napětí a nábojů na kondenzátorech při paralelním zapojení.
- Zjistěte, kolikrát se změní celkový náboj na kondenzátorech, pokud napětí zmenšíme na polovinu. Jak se změní náboje na jednotlivých kondenzátorech? Vyzkoušejte i další hodnoty celkového napětí a zformulujte, jak souvisí náboje s celkovým napětím.
Pozn. Posuvníky lze ovládat myší. Pohodlnější ale může být měnit hodnotu na vybraném posuvníku šipkami na klávesnici.
Dynamický prvek − sériové zapojení
Úlohy pro práci s apletem
- Měňte celkové napětí v obvodu. Pozorujte a popište, jak se mění napětí a náboj na obou kondenzátorech (v právé části jsou číselné hodnoty i jejich grafické znázornění).
- Nastavujte různé hodnoty kapacity kondenzátorů a pozorujte, zda a případně jak se na nich mění náboje.
- Nastavujte různé hodnoty kapacit obou kondenzátorů a pozorujte, jak se mění celková kapacita zapojení (číselná hodnota celkové kapacity je v levé části). Jaký vztah platí pro celkovou kapacitu?
- Pokračujte v předchozím úkolu a ověřte, zda pro celkové napětí platí vztah \(U=U_1 + U_2.\)
- Nastavte kapacity kondenzátorů v poměru 1:2 a pozorujte v jakém poměru na nich budou napětí. Vyzkoušejte i pro další jednoduché poměry. Na základě svých pozorování zformulujte závěry o tom, jak souvisí poměr kapacit s hodnotami napětí a nábojů na kondenzátorech při sériovém zapojení.
- Zjistěte, kolikrát se změní celkové napětí na kondenzátorech, pokud napětí zmenšíme na polovinu. Jak se změní napětí na jednotlivých kondenzátorech? Vyzkoušejte i další hodnoty celkového napětí a zformulujte, jak souvisí napětí s celkovým napětím.
Pozn. Lépe lze ovládat posuvník šipkami na klávesnici.



