Sbírka řešených úloh

Intenzita elektrického pole čtyř nábojů

Úloha číslo: 93

Čtyři náboje o velikostech

Q₁ = 5Q,

Q₂ = 5Q,

Q₃ = 3Q

Q₄ = −12Q

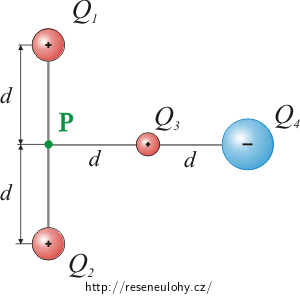
jsou uspořádány podle obrázku. Určete intenzitu elektrického pole v bodě P.

 

Pozn.: Na obrázku je schematicky znázorněna velikost nábojů.

• Nápověda: Výpočet celkové intenzity

  Celkovou intenzitu získáme vektorovým součtem intenzit od jednotlivých nábojů.

• Nápověda: Směr a velikost intenzity od jednoho náboje

  Elektrická intenzita má stejný směr jako síla, která by v daném místě působila na kladný náboj.

  Velikost elektrické intenzity v daném bodě je přímo úměrná velikosti náboje, který pole vytváří, a nepřímo úměrná druhé mocnině vzdálenosti od tohoto náboje.

• Obrázek

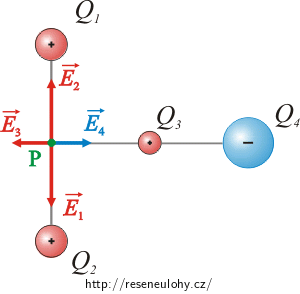
  Do obrázku zakreslíme směry vektorů elektrických intenzit od jednotlivých nábojů. Vektory elektrické intenzity kladných nábojů míří od náboje, elektrická intenzita záporného náboje míří k náboji.

  

• Rozbor

  Směr elektrické intenzity je stejný jako směr elektrické síly, která by v bodě P působila na kladný náboj. V případě kladných nábojů míří tedy elektrická intenzita směrem od náboje, v případě záporného naopak směrem k náboji.

  Velikost elektrické intenzity od jednoho náboje je přímo úměrná velikosti náboje, který pole vytváří, a nepřímo úměrná druhé mocnině vzdálenosti náboje.

  Celková elektrická intenzita v bodě P je dána vektorovým součtem elektrických intenzit od jednotlivých nábojů.

• Řešení úvahou

  Celkovou intenzitu v bodě P získáme vektorovým součtem intenzit od jednotlivých nábojů.

  Nejdříve se zaměřme na elektrickou intenzitu pole, které v bodě P vytváří první a druhý náboj. Náboje jsou stejně velké a stejně vzdálené od bodu P. Vektory elektrických intenzity od těchto nábojů budou mít tedy stejnou velikost. Oba náboje jsou kladné a jsou na opačných stranách od bodu P. Vektory intenzit budou mít tedy opačný směr, a proto se odečtou.

  Zbývají vektory elektrických intenzit od třetího a čtvrtého náboje. Vzdálenost náboje Q₄ od bodu P je dvakrát větší než vzdálenost náboje Q₃. Vektor elektrické intenzity od tohoto náboje by měl být tedy čtyřikrát menší, ale velikost náboje Q₄ je čtyřikrát větší. Oba tyto faktory se vyruší, a proto budou oba vektory elektrické intenzity stejně velké.

  Třetí náboj je kladný, vektor intenzity bude tedy směřovat od náboje (tj. z bodu P doleva). Čtvrtý náboj je záporný, intenzita bude tedy mířit k němu (tj. z bodu P doprava). Vektory intenzity jsou stejně velké a mají opačný směr, a proto se také odečtou.

  Celková intenzita v bodě P je tedy rovna nule.

• Řešení výpočtem

  Celkovou intenzitu v bodě P získáme vektorovým součtem intenzit od jednotlivých nábojů (viz obrázek):

  \[\vec{E}\,=\,\vec{E}_1+\vec{E}_2+\vec{E}_3+\vec{E}_4.\]

  Velikosti vektorů intenzit od jednotlivých nábojů vypočítáme ze vzorce:

  \[E\,=\,k\,\frac {Q} {r^2}\,\, ,\]

  kde Q je velikost daného náboje a r jeho vzdálenost od bodu P.

   

  Náboje Q₁ a Q₂ mají stejnou velikost 5Q a oba mají od bodu P vzdálenost d, vektory intenzity \(\vec{E}_1\) a \(\vec{E}_2\) jsou tedy stejně velké:

  \[E_1\,=\,E_2\,=\,k\,\frac {5Q} {d^2}.\]

  Na obrázku vidíme, že vektory mají opačný směr. Vektorový součet \(\vec{E}_1\) a \(\vec{E}_2\) je tedy roven nule:

  \[\vec{E}_1+\vec{E}_2\,=\,0.\]

  Nyní vypočteme velikosti intenzit \(\vec{E}_3\) a \(\vec{E}_4\):

  \[E_3\,=\,k\,\frac {3Q} {d^2},\] \[E_4\,=\,k\,\frac {12Q} {\left(2d\right)^2}\,=\,k\,\frac {12Q} {4d^2}\,=\,k\,\frac {3Q} {d^2}.\]

  Vektory intenzity \(\vec{E}_3\) a \(\vec{E}_4\) jsou opět stejně velké a mají opačný směr (viz obrázek), proto je jejich vektorový součet také roven nule:

  \[\vec{E}_3+\vec{E}_4\,=\,0.\]

  Celková elektrická intenzita v bodě P je tedy nulová.

• Odpověď

  Intenzita elektrického pole v bodě P je rovna nule.