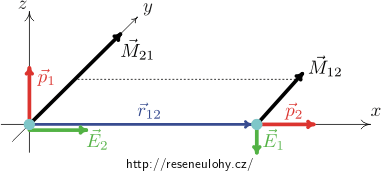
Vzájemné působení dvojice dipólů
Úloha číslo: 199
Dva ideální dipóly \(\vec p_1\), \(\vec p_2\) jsou umístěny ve vzdálenosti r způsobem nakresleným na obrázku.
Jaký je moment síly, kterým působí první dipól na druhý? Jaký je moment síly, kterým působí druhý dipól na první?
Nečekejte, že momenty sil budou stejně velké a opačného směru. Není tomu tak. Zákon akce a reakce platí pro síly, nikoli pro momenty sil.
Nápověda 1
Ideální dipól \(\vec p\) umístěný v počátku budí v místě \(\vec r\) elektrické pole, jehož intenzita je určena vztahem
\[{\vec E}({\vec r}) = \frac{1}{4\pi\varepsilon_0}\left(\frac{3({\vec p}\cdot {\vec r}){\vec r}}{r^5}-\frac{{\vec p}}{r^3}\right).\]Nápověda 2
Odvoďte si nebo najděte vztah pro moment síly působící na dipól v elektrickém poli.
Nápověda 3
Použijte vztah z druhé nápovědy pro moment síly působící na dipól v elektrickém poli. Uvědomte si, že do vztahu pro moment síly působící na první dipól je třeba dosadit
- dipólový moment prvního dipólu,
- vztah pro intenzitu buzenou druhým dipólem v místě dipólu prvního.
Analogicky do vztahu pro moment síly působící na druhý dipól je třeba dosadit
- dipólový moment druhého dipólu,
- vztah pro intenzitu buzenou prvním dipólem v místě dipólu druhého.
Nápověda 4
Po mechanickém dosazení do vztahu pro moment síly (viz nápověda 2 a 3) si uvědomte, že
v případě prvního dipólu jsou jeho dipólový moment \(\vec p_1\) a vektor spojující první a druhý dipól \(\vec r_{12}\) na sebe kolmé (a jejich skalární součin je nulový);
v případě druhého dipólu jsou jeho dipólový moment \(\vec p_2\) a vektor spojující druhý a první dipól \(\vec r_{21}\) rovnoběžné a opačně orientované vektory. Jeden tedy můžeme nahradit druhým, neboť například platí
\[\frac{\vec p_2}{p_2} = -\frac{\vec r_{21}}{r_{21}}.\]
(Po podělení vektorů jejich velikostmi dostáváme jednotkové vektory, znaménko minus vyjadřuje jejich opačnou orientaci.)
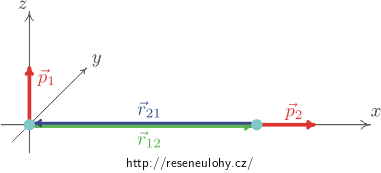
Rozbor
Oba dipóly samozřejmě považujeme za ideální. Ideální dipól umístěný v počátku soustavy souřadnic vytváří ve svém okolí pole o intenzitě
\[{\vec E}({\vec r}) = \frac{1}{4\pi\varepsilon_0}\left(\frac{3({\vec p}\cdot {\vec r}){\vec r}}{r^5}-\frac{{\vec p}}{r^3}\right).\]Toto pole pochopitelně působí na druhý dipól. Odvoďme, že obecně na dipól s dipólovým momentem \(\vec p\) působí moment síly \(\vec M\) v poli o intenzitě \(\vec E\) v místě dipólu:
\[{\vec M} = {\vec r}\times {\vec F} = {\vec r}\times {q\vec E} = {q\vec r}\times {\vec E} = {\vec p}\times {\vec E}.\]Vztahy nyní stačí vhodně zkombinovat, matematicky upravit a interpretovat výsledek.
Přitom podstatně využijeme toho, jak jsou dipóly vůči sobě umístěny!
Řešení
Dipóly umístíme do souřadné soustavy tak, že dipól \(\vec p_1\) je umístěn v počátku a míří ve směru kladné poloosy z, dipól \(\vec p_2\) je na kladné poloose x ve vzdálenosti r a míří ve směru kladné poloosy x (viz obrázek).
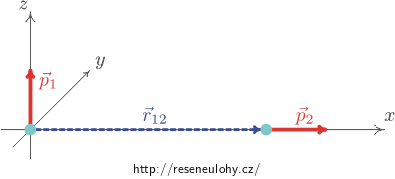
Působení prvního dipólu na druhý
Vektorem \(\vec r_{12}\) míníme vektor od prvního dipólu k druhému, jako vektor \(\vec r_{21} = -\vec r_{12}\) označíme vektor od druhého dipólu k prvnímu. Pochopitelně platí, že velikost obou je rovna vzdálenosti dipólů r.
Pak dipól \(\vec p_1\) působí momentem síly \(\vec M_{12}\) na dipól \(\vec p_2\) a platí
\[\vec M_{12} = \vec p_2 \times \vec E_1,\]kde \(\vec E_1\) značí intenzitu elektrického pole vyvolaného prvním dipólem v místě dipólu druhého. Pro intenzitu \(\vec E_1\) platí, že
\[{\vec E_1}({\vec r_{12}}) = \frac{1}{4\pi\varepsilon_0}\left(\frac{3({\vec p_1}\cdot {\vec r_{12}}){\vec r_{12}}}{r_{12}^5}-\frac{{\vec p_1}}{r_{12}^3}\right)\]a protože vektory \(\vec p_1\) a \(\vec r_{12}\) jsou na sebe kolmé, je skalární součin v prvním členu nulový a dostáváme
\[{\vec E_1}({\vec r_{12}}) = -\frac{1}{4\pi\varepsilon_0}\frac{{\vec p_1}}{r_{12}^3}.\]Vektor \(\vec E_1\) je tedy opačně orientován než vektor \(\vec p_1\), míří svisle dolů, ve směru záporné poloosy z.
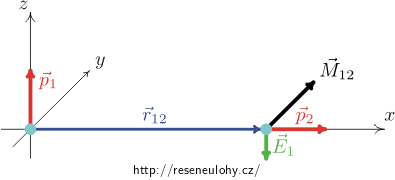
Proto \(\vec M_{12}\) míří podle pravidla pravé ruky ve směru kladné poloosy y a má velikost
\[M_{12} = p_2\cdot \frac{p_1}{4\pi\varepsilon_0 r_{12}^3} = \frac{p_1p_2}{4\pi\varepsilon_0r^3}.\]Působení druhého dipólu na první
Oproti tomu dipól \(\vec p_2\) působí momentem síly \(\vec M_{21}\) na dipól \(\vec p_1\) a platí
\[\vec M_{21} = \vec p_1 \times \vec E_2,\]kde platí
\[{\vec E_2}({\vec r_{21}}) = \frac{1}{4\pi\varepsilon_0}\left(\frac{3({\vec p_2}\cdot {\vec r_{21}}){\vec r_{21}}}{r_{21}^5}-\frac{{\vec p_2}}{r_{21}^3}\right)\]a protože vektory \(\vec p_2\) a \(\vec r_{21}\) mají stejný směr a opačnou orientaci, platí
\[\vec p_2 \cdot \vec r_{21} = -p_2r_{21}\]a dále
\[\vec p_2 = p_2\, \left(\frac{-\vec r_{21}}{r_{21}}\right), \qquad {\rm nebo} \qquad -p_2\vec r_{21} = r_{21}\vec p_2.\]S využitím těchto vztahů dostaneme
\[{\vec{E_2}}({\vec{r_{21}}}) = \frac{1}{4\pi\varepsilon_0}\left(-\frac{3p_2r_{21}{\vec r_{21}}}{r_{21}^5}-\frac{p_2}{r_{21}^3}\,\left(\frac{-\vec r_{21}}{r_{21}}\right)\right.\]a díky předchozí rovnosti \(-p_2\vec r_{21} = r_{21}\vec p_2\) můžeme vztah upravit do tvaru
\[{\vec E_2}({\vec r_{21}}) = \frac{1}{4\pi\varepsilon_0}\frac{2\vec p_2}{r_{21}^3}.\]Odtud je zřejmé, že vektor \(\vec E_2\) míří ve směru doprava, to jest, ve směru kladné poloosy x a má velikost
\[E_2 = \frac{2p_2}{4\pi\varepsilon_0 r^3}.\]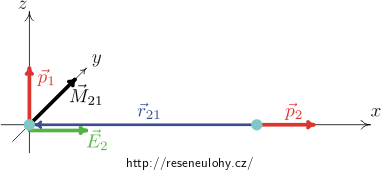
Proto vektor \(\vec M_{21}\) míří podle pravidla pravé ruky opět ve směru kladné poloosy y a má velikost
\[M_{21} = \frac{2p_1p_2}{4\pi\varepsilon_0 r^3}.\]Všimněte si, že oba momenty mají stejný směr a orientaci a rozdílnou velikost. O spor se zákonem akce a reakce nejde; ten hovoří o silách a navíc situace zdaleka není symetrická — vektor spojující oba dipóly je s jedním momentem rovnoběžný, zatímco na druhý je kolmý.
Výsledek
Moment síly \(\vec M_{12}\), kterým první dipól působí na druhý, míří ve směru kladné poloosy y a má velikost
\[M_{12} = \frac{p_1p_2}{4\pi\varepsilon_0 r^3}.\]Moment síly \(\vec M_{21}\), kterým druhý dipól působí na první, míří ve směru kladné poloosy y a má velikost
\[M_{21} = \frac{2p_1p_2}{4\pi\varepsilon_0 r^3}.\]