Dvojice rovnoběžných nabitých rovin
Úloha číslo: 482
Dvojice rovnoběžných rovin, jejichž vzdálenost je d, je nabita nábojem se stejně velkou plošnou hustotou σ.
Určete průběh intenzity elektrického pole těchto rovin.
Určete potenciál elektrického pole těchto rovin.
Pozn.: Roviny mohou být nabity nábojem stejného nebo opačného znaménka. Řešte oba případy.
Nápověda 1: Pomocná úloha
Zkuste nejprve vyřešit úlohu Pole rovnoměrně nabité roviny a využijte výsledků a grafů této úlohy.
Nápověda 2
Jestliže víme, jak vypadá pole v okolí nabité roviny, můžeme s využitím principu superpozice jejich sečtením zjistit, jak vypadá pole dvou rovnoběžných rovin.
Nakreslete si obrázek.
Řešení: Roviny nabité opačnými náboji
Nejprve budeme uvažovat, že jedna rovina je nabita kladným nábojem, a druhá záporným.
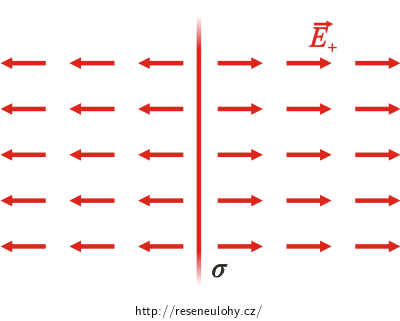
Využijeme výsledek úlohy Pole rovnoměrně nabité roviny, ve které jsme zjistili, že jedna nabitá rovina kolem sebe vytváří homogenní pole s intenzitou
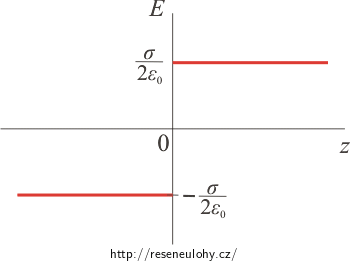
\[E_1\,=\, \frac{\sigma}{2\varepsilon_0}\,. \]Pokud je rovina nabita kladným nábojem, míří vektor elektrické intenzity ve všech místech od roviny. Pokud je rovina nabita záporným nábojem, míří vektor k rovině. Protože obě roviny jsou nabity se stejnou nábojovou hustotou, mají intenzity od obou rovin stejnou velikost.
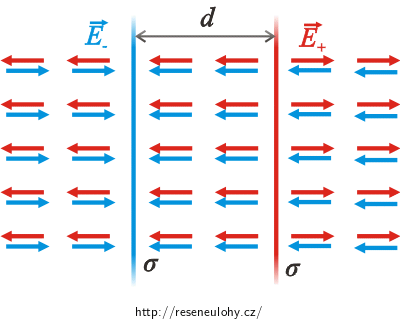
Nakreslíme obrázek naší situace a zakreslíme vektory elektrických intenzit od každé roviny (podrobnější obrázek je uveden v řešení druhé nápovědy).
Vně rovin míří vektory elektrických intenzit opačným směrem, elektrické pole se zde tedy ruší a intenzita je rovna nule. Mezi rovinami míří vektory stejným směrem, výsledná intenzita bude tedy dvojnásobná.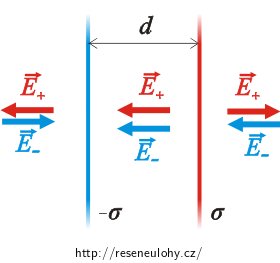
Máme-li dvě rovnoběžné roviny nabité opačným nábojem, vzniká mezi nimi homogenní elektrické pole o intenzitě
\[E\,=\,\frac{\sigma}{\varepsilon_0}\,.\]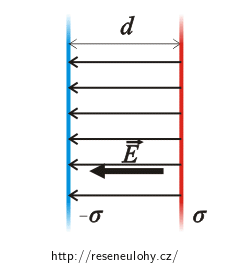
Tohoto uspořádání využíváme při konstrukci kondenzátorů.
Řešení: Roviny nabité stejnými náboji
Nyní uvažujeme, že jsou obě roviny nabity nábojem stejného znaménka, například kladným nábojem. (Pozn.: Pro záporný náboj by vektor elektrické intenzity měl pouze opačný směr.)
Opět využijeme výsledek úlohy Pole rovnoměrně nabité roviny a nakreslíme si obrázek.
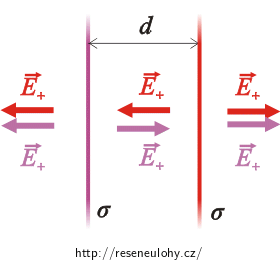
Tentokrát je situace opačná, než v případě rovin nabitých opačným nábojem. Mezi rovinami mají vektory intenzit opačný směr, a proto se zde elektrické pole ruší. Vně rovin mají intenzity stejný směr, vzniká tedy homogenní elektrické pole s intenzitou
\[E\,=\,\frac{\sigma}{\varepsilon_0}\,.\]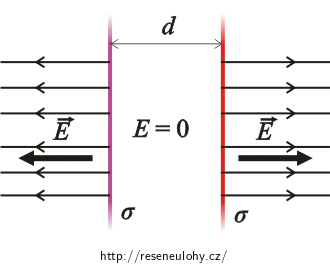
Řešení: Intenzita graficky – opačně nabité roviny
V tomto oddíle určíme průběh intenzity pole dvou rovin pomocí grafů.
Nejdříve zakreslíme do jednoho grafu průběh intenzity elektrického pole pro každou rovinu zvlášť. Využijeme přitom grafu z úlohy Pole rovnoměrně nabité roviny.
Pro kladně nabitou rovinu je grafem po částech konstantní funkce, která v místě roviny, tj. v bodě z = d/2, mění znaménko. Na kladné části osy z je kladná a na většině záporné části je záporná (průběh je zakreslen červeně).
Pro záporně nabitou rovinu mění po částech konstantní funkce znaménko v bodě z = −d/2. Díky opačnému znaménku je oproti předchozí situaci na většině kladné osy z záporná a na záporné části osy kladná (zakresleno modře).
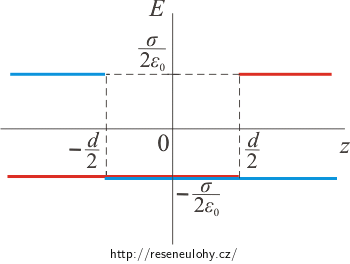
Nyní funkce na jednotlivých intervalech sečteme. Mezi rovinami mají obě konstantní funkce hodnotu \(-\frac{\sigma}{2 \varepsilon_0}\). Jejich sečtením vznikne konstantní funkce s dvojnásobnou hodnotou. Vně rovin mají konstantní funkce pro obě roviny opačné znaménko, sečtením dostaneme tedy nulovou funkci.
Řešení: Intenzita graficky – kladně nabité roviny
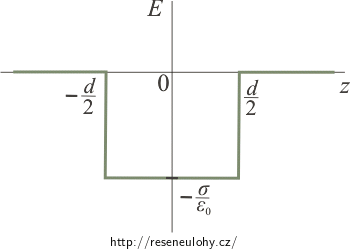
V tomto oddíle určíme průběh intenzity pomocí grafů pro roviny nabité nábojem se stejným znaménkem. Budeme uvažovat náboj kladný.
Postup bude úplně stejný jako pro opačně nabité roviny v předchozím oddíle. Nejdříve zakreslíme do jednoho grafu průběh intenzity elektrického pole pro každou rovinu zvlášť. Využijeme přitom graf z úlohy Pole rovnoměrně nabité roviny.
Mezi rovinami, tedy na intervalu \(\lt-\frac{d}{2};\frac{d}{2}\gt\), mají konstantní funkce opačné znaménko. Sečtením nám tedy vznikne nulová funkce. Na zbylých intervalech mají obě konstantní funkce vždy stejné znaménko i hodnotu. Jejich sečtením vznikne opět konstantní funkce, ale s dvojnásobnou hodnotou, která bude buď kladná, pokud jsme sčítali kladné funkce, nebo záporná tam, kde jsme sčítali záporné funkce.
Řešení: Potenciál graficky – opačně nabité roviny
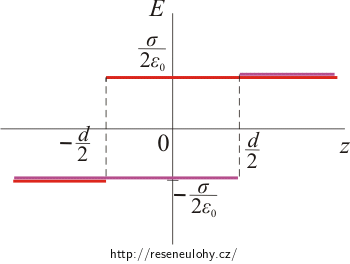
Nyní nakreslíme grafy pro potenciál. Nejdříve opět do jednoho grafu pro obě roviny zvlášť. Grafy upravíme tak, aby obě funkce měly nulový potenciál ve stejném místě, například na záporně nabité rovině.
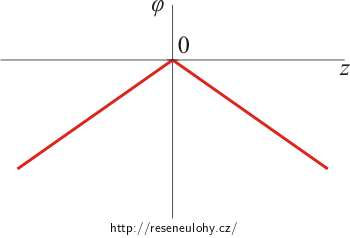
Pro záporně nabitou rovinu je potenciál roven nule na rovině. Funkce nejdříve lineárně klesá a poté lineárně roste. V grafu je funkce zakreslena modře:
\[\varphi_- (z)\,=\, \frac{\sigma}{2\varepsilon_0} |z\,+\,\frac{d}{2}|.\]Pro kladně nabitou rovinu potenciál nejdříve lineárně roste a poté lineárně klesá. Aby byl potenciál roven nule v místě záporné roviny, musíme celý graf funkce posunout nahoru tak, aby přímka protínala osu z v bodě \(-\frac{d}{2}\). V grafu je funkce zakreslena červeně:
\[\varphi_+ (z)\,=\, -\frac{\sigma}{2\varepsilon_0} |z\,-\,\frac{d}{2}|\,+\,\frac{\sigma d}{2\varepsilon_0}.\]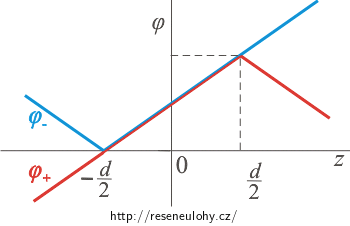
Na následujícím obrázku je zeleně zakreslena výsledná funkce, která vznikne sečtením obou potenciálů.
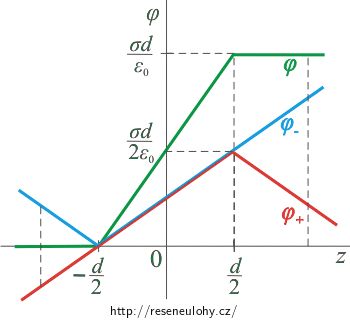
Na intervalu mezi rovinami budeme sčítat dvě lineární funkce, které mají stejnou směrnici. Výsledkem bude opět lineární funkce, která bude mít směrnici dvojnásobnou (tzn. bude „růst“ rychleji):
\[\varphi (z)\,=\, \,\frac{\sigma}{\varepsilon_0}\,\left(z\, +\, \frac{d}{2}\right).\]Vně rovin mají lineární funkce pro jednotlivé roviny stejně velké směrnice, ale opačného znaménka. Po jejich sečtení nám vyjde konstantní funkce, která je pro záporná z rovna nule a pro kladná z má hodnotu \(\frac{\sigma d}{\varepsilon_0}\).
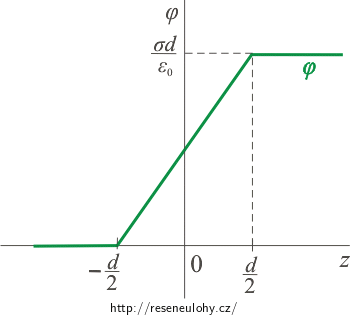
Zkusme určit potenciál i algebraickým sečtením obou funkcí:
\[\varphi (z)\,=\,\varphi_- (z)\,+\,\varphi_+ (z),\] \[\varphi (z)\,=\,\frac{\sigma}{2\varepsilon_0} |z\,+\,\frac{d}{2}| \,-\,\frac{\sigma}{2\varepsilon_0} |z\,-\,\frac{d}{2}|\,+\,\frac{\sigma d}{2\varepsilon_0}.\]Výpočet provedeme postupně pro všechny tři části prostoru, v každé si musíme rozmyslet, jaká znaménka mají výrazy v absolutní hodnotě ve vyjádření obou potenciálů.
1) Vpravo od rovin, tj. pro z > d/2
Oba výrazy v absolutních hodnotách jsou kladné, dostáváme tedy:
\[\varphi (z)\,=\,\frac{\sigma}{2 \varepsilon_0}\,\left(z\,+\, \frac{d}{2}\right) \,-\,\frac{\sigma}{2 \varepsilon_0}\,\left(z\,-\, \frac{d}{2}\right)\,+\, \frac{\sigma}{2 \varepsilon_0}d,\] \[\varphi (z)\,=\,\frac{\sigma}{2 \varepsilon_0}\left(z\,+\, \frac{d}{2} \,-\,z\, +\, \frac{d}{2}\,+\, d \right), \] \[\varphi (z)\,=\,\frac{\sigma}{\varepsilon_0}d.\]2) Mezi rovinami, tj. pro −d/2 < z < d/2
Výraz v první absolutní hodnotě je kladný, ve druhé záporný, dostáváme tedy:
\[\varphi (z)\,=\,\frac{\sigma}{2 \varepsilon_0}\,\left(z\,+\, \frac{d}{2}\right) \,-\,\frac{\sigma}{2 \varepsilon_0}\,\left[-\left(z\,-\, \frac{d}{2}\right)\right]\,+\, \frac{\sigma}{2 \varepsilon_0}d,\] \[\varphi (z)\,=\,\frac{\sigma}{2 \varepsilon_0}\left(z\,+\, \frac{d}{2} \,+\,z\, -\, \frac{d}{2}\,+\, d \right),\] \[\varphi (z)\,=\,\frac{\sigma}{\varepsilon_0}\left(z\,+\, \frac{d}{2} \right).\]3) Vlevo od rovin, tj. pro z < −d/2
Výrazy v obou absolutních hodnotách jsou záporné, dostáváme tedy:
\[\varphi (z)\,=\,\frac{\sigma}{2 \varepsilon_0}\,\left[-\left(z\,+\, \frac{d}{2}\right)\right] \,-\,\frac{\sigma}{2 \varepsilon_0}\,\left[-\left(z\,-\, \frac{d}{2}\right)\right]\,+\, \frac{\sigma}{2 \varepsilon_0}d,\] \[\varphi (z)\,=\,\frac{\sigma}{2 \varepsilon_0}\left(-z\,-\, \frac{d}{2} \,+\,z\, -\, \frac{d}{2}\,+\, d \right),\] \[\varphi (z)\,=\,0.\]Vidíme, že nám potenciál vyšel stejně jako grafickým sčítáním grafů obou funkcí.
Spočteme ještě napětí mezi rovinami, které je rovno rozdílu potenciálů na obou rovinách:
\[U\,=\,\varphi (\frac{d}{2})\,-\,\varphi (-\frac{d}{2})\,=\, \frac{\sigma}{\varepsilon_0}\,d\,-\,0=\, \frac{\sigma}{\varepsilon_0}\,d\,=\,Ed.\]Tento vztah známe z úloh, které se týkají deskového kondenzátoru.
Řešení: Potenciál graficky – kladně nabité roviny
Budeme postupovat podobně jako v předchozím oddílu.
Nejdříve zakreslíme do grafu potenciál pro jednotlivé roviny. Protože jsou obě roviny nabity stejným nábojem, mají také stejný průběh potenciálu. Grafy jsou akorát různě posunuté ve svislém směru, aby obě funkce měly nulový potenciál ve stejném místě. Nejdříve potenciál lineárně roste. Na rovině je potenciál maximální a poté lineárně klesá:
\[\varphi_1 (z)\,=\, -\frac{\sigma}{2\varepsilon_0} |z\,+\,\frac{d}{2}|.\]Graf pro druhou rovinu musíme posunout nahoru tak, aby protínal osu z v bodě −d/2:
\[\varphi_2 (z)\,=\, -\frac{\sigma}{2\varepsilon_0} |z\,-\,\frac{d}{2}|\, + \,\frac{\sigma d}{2 \varepsilon_0}.\]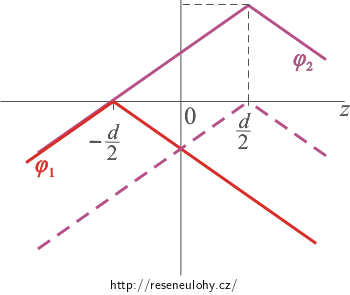
Na následujícím obrázku je zeleně zakreslena výsledná funkce, která vznikne sečtením potenciálů.
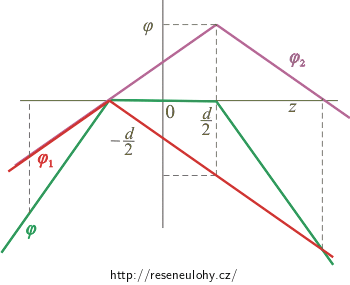
Mezi rovinami (tedy na intervalu \(\lt-\frac{d}{2};\frac{d}{2}\gt\)) sčítáme dvě lineární funkce, které mají stejné směrnice opačného znaménka. Výsledkem je konstantní funkce. Na ostatních intervalech sčítáme vždy dvě lineární funkce, které mají stejnou směrnici. Jejich složením vznikne opět lineární funkce, která má ale dvojnásobnou směrnici.
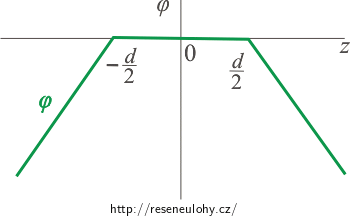
Pokud chceme nulový potenciál jinde než na levé rovině, stačí celý graf posunout ve svislém směru.
Zkusme určit potenciál i algebraickým sečtením obou funkcí:
\[\varphi (z)\,=\,\varphi_1 (z)\,+\,\varphi_2 (z),\] \[\varphi (z)\,=\,-\frac{\sigma}{2\varepsilon_0} |z\,+\,\frac{d}{2}|\,+\,-\frac{\sigma}{2\varepsilon_0} |z\,-\,\frac{d}{2}|\, + \,\frac{\sigma d}{2 \varepsilon_0}.\]Výpočet provedeme postupně pro všechny tři části prostoru, v každé si musíme rozmyslet, jaká znaménka mají výrazy v absolutních hodnotách.
1) Vpravo od rovin, tj. pro z > d/2
Oba výrazy v absolutních hodnotách jsou kladné, dostáváme tedy:
\[\varphi (z)\,=\,-\frac{\sigma}{2 \varepsilon_0}\,\left(z\,+\, \frac{d}{2}\right) \,-\,\frac{\sigma}{2 \varepsilon_0}\,\left(z\,-\, \frac{d}{2}\right)\,+\, \frac{\sigma}{2 \varepsilon_0}d,\] \[\varphi (z)\,=\,\frac{\sigma}{2 \varepsilon_0}\left(-z\,-\, \frac{d}{2}\,-\,z\, +\, \frac{d}{2}\,+\, d \right) ,\] \[\varphi (z)\,=\,-\frac{\sigma}{\varepsilon_0}\,\left(z\,-\, \frac{d}{2}\right).\]2) Mezi rovinami, tj. pro −d/2 < z < d/2
Výraz v první absolutní hodnotě je kladný, ve druhé záporný, dostáváme tedy:
\[\varphi (z)\,=\,-\frac{\sigma}{2 \varepsilon_0}\,\left(z\,+\, \frac{d}{2}\right) \,-\,\frac{\sigma}{2 \varepsilon_0}\,\left[-\left(z\,-\, \frac{d}{2}\right)\right]\,+\, \frac{\sigma}{2 \varepsilon_0}d,\] \[\varphi (z)\,=\,\frac{\sigma}{2 \varepsilon_0}\left(-z\,-\, \frac{d}{2} \,+\,z\, -\, \frac{d}{2}\,+\, d \right),\] \[\varphi (z)\,=\,0.\]3) Vlevo od rovin, tj. pro z < −d/2
Výrazy v obou absolutních hodnotách jsou záporné, dostáváme tedy:
\[\varphi (z)\,=\,-\frac{\sigma}{2 \varepsilon_0}\,\left[-\left(z\,+\, \frac{d}{2}\right)\right] \,-\,\frac{\sigma}{2 \varepsilon_0}\,\left[-\left(z\,-\, \frac{d}{2}\right)\right]\,+\, \frac{\sigma}{2 \varepsilon_0}d,\] \[\varphi (z)\,=\,\frac{\sigma}{2 \varepsilon_0}\left(z\,+\, \frac{d}{2} \,+\,z\, -\, \frac{d}{2}\,+\, d \right),\] \[\varphi (z)\,=\,\frac{\sigma}{\varepsilon_0}\left(z\,+\, \frac{d}{2}\right).\]Vidíme, že nám potenciál vyšel stejně jako grafickým sčítáním grafů obou funkcí.
Řešení: Potenciál integrováním, intenzita derivací
Pokud známe průběh intenzity E, můžeme potenciál φ vypočítat také pomocí integrálu. Velikost potenciálu je rovna integrálu z intenzity.
\[\varphi\,=\, -\,\int_\mathrm{A}^\mathrm{B} \vec{E}\cdot \mathrm{d}\vec {z}\,,\]kde A je místo s nulovým potenciálem a B je místo, kde potenciál zjišťujeme.
Na druhou stranu, pokud známe průběh potenciálu φ v prostoru, můžeme intenzitu E určit pomocí gradientu, tj. pomocí derivací. Pro intenzitu E platí
\[\vec{E} = - \mathrm{grad} \varphi \,,\]což pro jednotlivé složky intenzity dává
\[E_\mathrm{x} = - \frac{\partial \varphi}{\partial x}\,, \qquad E_\mathrm{y} = - \frac{\partial \varphi}{\partial y}\,, \qquad E_\mathrm{z} = - \frac{\partial \varphi}{\partial z}\,.\]Opačně nabité roviny – integrací od intenzity k potenciálu
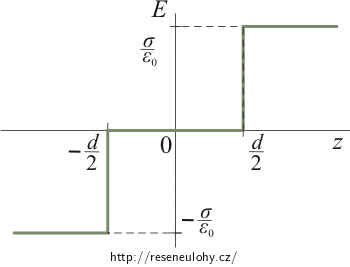
Nulový potenciál zvolíme na záporné rovině.
Nalevo od této roviny je intenzita rovna nule, proto bude i potenciál stále roven nule. („Integrujeme-li nulu, vyjde nám opět nula.“)
Napravo od záporně nabité roviny (tzn. mezi rovinami) je intenzita konstantní a rovna \(\frac{\sigma}{\varepsilon_0}\). Integrujeme-li konstantní funkci, vyjde nám funkce lineární, která bude mít směrnici rovnou této konstantě. Potenciál bude tedy lineárně růst od nuly (na záporně nabité rovině) až po hodnotu \(\frac{\sigma}{\varepsilon_0} d\) v bodě \(\frac{d}{2}\) (na kladně nabité rovině):
\[\varphi (z)\,=\, - \int_\mathrm{-\frac{d}{2}}^\mathrm{z} E\,\mathrm{d}z\,=\, - \int_\mathrm{-\frac{d}{2}}^\mathrm{z} - \frac{\sigma}{\varepsilon_0}\,\mathrm{d}z\,=\, \frac{\sigma}{\varepsilon_0}\,\int_\mathrm{-\frac{d}{2}}^\mathrm{z} \mathrm{d}z\,=\, \frac{\sigma}{\varepsilon_0}\,[z]_\mathrm{-\frac{d}{2}}^\mathrm{z}, \] \[\varphi (z)\,=\, \frac{\sigma}{\varepsilon_0}\,\left(z\,-\,\frac{d}{2}\right). \]Za kladnou rovinou je intenzita opět rovna nule, a proto potenciál už dále růst nebude a bude stejný jako na kladně nabité rovině.
Na následujícím obrázku je vše zakresleno do grafu.
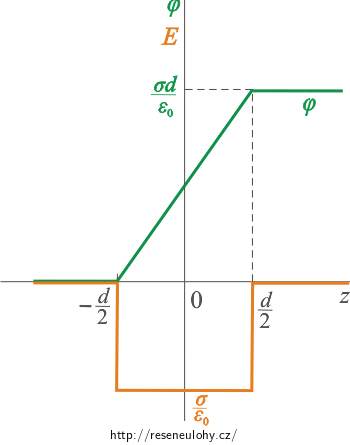
Opačně nabité roviny – derivováním od potenciálu k intenzitě
Nejprve si všimneme, že potenciál závisí pouze na souřadnici z, tj. intenzita bude mít nenulovou pouze z-ovou složku.
V prostoru mimo roviny je potenciál konstantní, proto jeho derivace bude nulová, tj. i intenzita v těchto místech bude nulová (viz obrázek výše). Mezi rovinami dostáváme:
\[E_\mathrm{z}\,=\, - \,\frac{\partial}{\partial z}\, \left( \frac{\sigma}{\varepsilon_0} \left( z\,+\,\frac{d}{2}\right)\right)\,=\, -\, \frac{\partial}{\partial z}\, \frac{\sigma z}{\varepsilon_0} \,-\, \frac{\partial}{\partial z}\, \frac{\sigma d}{\varepsilon_0 2},\] \[ E_\mathrm{z}\,=\, - \, \frac{\sigma}{\varepsilon_0}.\]Kladně nabité roviny – integrací od intenzity k potenciálu
Pro kladně nabité roviny budeme postupovat podobně.
Nulový potenciál zvolíme na levé rovině. Napravo od této roviny (tzn. mezi rovinami) je intenzita rovna nule, a proto se ani potenciál nebude měnit a bude zde roven nule. Vně rovin je intenzita konstantní a je rovna \(\pm\,\frac{\sigma}{\varepsilon_0}\), potenciál bude tedy směrem od rovin lineárně klesat se směrnicí rovnou této konstantě.
Pro z < −d/2 tedy dostáváme:
\[\varphi (z)\,=\, - \int_\mathrm{-\frac{d}{2}}^\mathrm{z} E\,\mathrm{d}z\,=\, - \int_\mathrm{-\frac{d}{2}}^\mathrm{z} - \frac{\sigma}{\varepsilon_0}\,\mathrm{d}z\,=\, \frac{\sigma}{\varepsilon_0}\,[z]_\mathrm{-\frac{d}{2}}^\mathrm{z}, \] \[\varphi (z)\,=\, -\frac{\sigma}{\varepsilon_0}\,\left(z\,+\,\frac{d}{2}\right). \]Pro z > d/2 dostáváme:
\[\varphi (z)\,=\, - \int_\mathrm{-\frac{d}{2}}^\mathrm{z} E\,\mathrm{d}z\,=\, -\int_\mathrm{-\frac{d}{2}}^{\frac{d}{2}}0\,\mathrm{d}z\,-\, \int_\mathrm{\frac{d}{2}}^\mathrm{z} \frac{\sigma}{\varepsilon_0}\,\mathrm{d}z\,=\, -\frac{\sigma}{\varepsilon_0}\,[z]_\mathrm{\frac{d}{2}}^\mathrm{z}, \] \[\varphi (z)\,=\, \frac{\sigma}{\varepsilon_0}\,\left(z\,-\,\frac{d}{2}\right). \]Na následujícím obrázku je opět vše zakresleno do grafu.
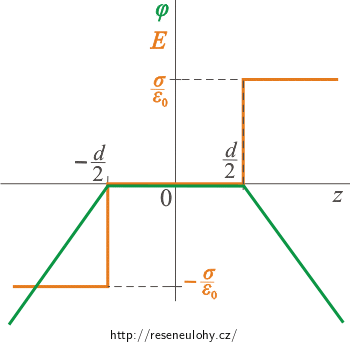
Kladně nabité roviny – derivováním od potenciálu k intenzitě
Potenciál opět závisí pouze na souřadnici z, tj. intenzita bude mít nenulovou pouze z-ovou složku.
V prostoru mezi rovinami je potenciál konstantní, proto jeho derivace bude nulová, tj. i intenzita v těchto místech bude nulová (viz obrázek výše).
Nalevo od rovin, tj. pro z < −d/2, dostáváme:
\[E_\mathrm{z}\,=\, - \,\frac{\partial}{\partial z}\, \left( \frac{\sigma}{\varepsilon_0} \left( z\,+\,\frac{d}{2}\right)\right)\,=\, -\, \frac{\partial}{\partial z}\, \frac{\sigma z}{\varepsilon_0} \,-\, \frac{\partial}{\partial z}\, \frac{\sigma d}{\varepsilon_0 2},\] \[ E_\mathrm{z}\,=\, - \, \frac{\sigma}{\varepsilon_0}.\]Nalevo od rovin, tj. pro z > d/2, dostáváme:
\[E_\mathrm{z}\,=\, - \,\frac{\partial}{\partial z}\, \left( -\frac{\sigma}{\varepsilon_0} \left( z\,-\,\frac{d}{2}\right)\right)\,=\, \frac{\partial}{\partial z}\, \frac{\sigma z}{\varepsilon_0} \,-\, \frac{\partial}{\partial z}\, \frac{\sigma d}{\varepsilon_0 2},\] \[ E_\mathrm{z}\,=\, \frac{\sigma}{\varepsilon_0}.\]Odpověď
Opačně nabité roviny:
Vektor elektrické intenzity mezi rovinami míří od kladně nabité roviny k záporně nabité rovině a má velikost \(E\,=\,\frac{\sigma}{\varepsilon_0}\). Vně rovin je intenzita elektrického pole rovna nule.
Potenciál mezi rovinami se vzdáleností od záporné lineárně roste: \(\varphi (z)\,=\, \frac{\sigma}{\epsilon_0}\,\left(z\,+\,\frac{d}{2}\right)\). Vně rovin je pak potenciál konstantní a stejný jako na bližší rovině.
Tohoto uspořádání rovin využíváme při konstrukci kondenzátorů.
Dvě kladně nabité roviny:
Intenzita mezi rovinami je rovna nule. Vektory intenzity vně rovin míří směrem od rovin. Jejich velikost je \(E\,=\,\frac{\sigma}{\varepsilon_0}\).
Potenciál mezi rovinami je konstantní a většinou ho volíme roven nule. Vně rovin potenciál se vzdáleností lineárně klesá.
Pro z < −d/2 (tj. vlevo od obou rovin): \(\varphi (z)\,=\, \frac{\sigma}{\epsilon_0}\,\left(z\,+\,\frac{d}{2}\right)\).
Pro z > d/2 (tj. vpravo od obou rovin): \(\varphi (z)\,=\, -\frac{\sigma}{\epsilon_0}\,\left(z\,-\,\frac{d}{2}\right)\).