Sbírka řešených úloh

Elektrický stožár

Úloha číslo: 702

Elektrický stožár vysokého napětí 400 kV je uzemněný vodivou koulí o poloměru 30 cm, jež je z poloviny zakopána v zemi. Na vedení vznikla porucha tak, že nastal zkrat mezi stožárem a vedením. Určete pod jakým napětím se ocitne člověk, který udělá krok o délce 80 cm ve vzdálenosti 100 m od stožáru směrem k němu.

• Nápověda 1

  Nejprve vypočítejte odpor země kolem uzemnění. Jak velký bude proud, který poteče do země?

• Řešení nápovědy 1

  Elektrický odpor vodiče R je nepřímo úměrný vodivosti materiálu σ. Velikost elektrického odporu vypočítáme podle vztahu:

  \[ R\,=\,\frac{1}{\sigma}\,\frac{l}{S}\,, \]

  kde l je délka vodiče a S je obsah jeho průřezu.

  Elektrický stožár je uzemněný vodivou koulí o poloměru r₀, která je z poloviny zakopána v zemi. Celkový odpor země kolem uzemnění tedy vypočítáme tak, že si vytkneme polokulovou vrstvu země ve vzdálenosti r > r₀ o „délce“ dr a „ploše“ 2πr² a určíme, jak tato vrstva přispívá k celkovému odporu:

  \[ \mathrm{d}R\,=\,\frac{1}{\sigma}\,\frac{\mathrm{d}r}{2\pi r^2}\,. \]

  Celkový odpor poté určíme integrací od r₀ do nekonečna:

  \[ R\,=\,\int{\mathrm{d}R}\,=\,\int_\mathrm{r_0}^{\infty}{\frac{1}{\sigma}\,\frac{\mathrm{d}r}{2\pi r^2}}\,=\,\frac{1}{2\sigma\pi}\,\left[-\,\frac{1}{r}\right]_\mathrm{r_0}^{\infty}\,=\,\frac{1}{2\sigma\pi r_0}\,. \]

  Celkový proud I, který poteče do země kolem uzemnění, vypočítáme z Ohmova zákona:

  \[ I\,=\,\frac{U}{R}\,, \]

  kde U je napětí na elektrickém stožáru a R je celkový odpor uzemnění. Tedy:

  \[ I\,=\,2U\sigma\pi r_0\,. \]

• Nápověda 2

  Zjistěte, jaká je proudová hustota ve vzdálenosti r od stožáru.

• Řešení nápovědy 2

  Při výpočtu odporu země kolem uzemnění jsme si zemi kolem stožáru rozdělili na polokulové vrstvy. Z kulové symetrie situace vyplývá, že ve všech místech takové vrstvy je stejná hustota proudu j. Tuto proudovou hustotu určíme ze vztahu:

  \[ j\left(r\right)\,=\,\frac{I}{S}\,=\,\frac{I}{2\pi r^2}\,, \]

  kde 2πr² je plocha polokulové vrstvy a I je celkový proud tekoucí do uzemnění.

• Nápověda 3

  Vztah mezi proudem a napětím popisuje Ohmův zákon. Uvědomte si nebo vyhledejte, jak vypadá v diferenciálním tvaru.

• Řešení nápovědy 3

  Ohmův zákon pro homogenní vodiče v diferenciálním tvaru je dán vztahem

  \[ \vec{j\,}\,=\,\sigma\vec{E}\,, \]

  kde \(\vec{j\,}\) je hustota elektrického proudu, σ měrná elektrická vodivost a \(\vec{E}\) značí intenzitu elektrického pole.

• Nápověda 4

  Pomocí intenzity elektrického pole určete velikost napětí mezi dvěma body tohoto pole.

• Řešení nápovědy 4

  Pro napětí mezi dvěma body A, B elektrického pole platí vztah

  \[ U\,=\,\int_\mathrm{A}^\mathrm{B}{\vec{E}\cdot\mathrm{d}\vec{r\,}}\,. \]

  Podrobnější vysvětlení naleznete v oddíle úlohy Elektrický proud mezi válcovými elektrodami, Řešení nápovědy 2.

• Rozbor

  Pro jednoduchost budeme předpokládat kulovou symetrii situace.

  Zemi kolem stožáru si rozdělíme na polokulové vrstvy a vypočítáme celkový odpor země kolem uzemnění.

  

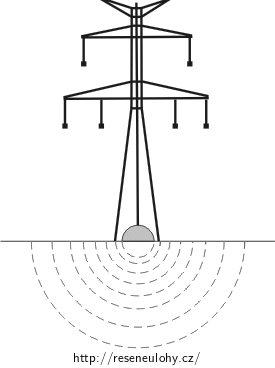
  Z kulové symetrie situace vyplývá, že ve všech místech jedné takové vrstvy je konstantní hustota proudu. Tu určíme za pomoci Ohmova zákona ze známého napětí na elektrickém stožáru a z celkového odporu země kolem uzemnění.

  Z Ohmova zákon pro homogenní vodiče v diferenciálním tvaru si vyjádříme intenzitu elektrického pole. Napětí, pod kterým se člověk vyskytne, pak získáme integrací intenzity elektrického pole.

• Řešení

  Nejprve vypočítáme celkový odpor země kolem uzemnění. Při tom budeme postupovat tak, že si vytkneme polokulovou vrstvu země ve vzdálenosti r > r₀ o tloušťce dr a určíme, jak tato vrstva přispívá k celkovému odporu. Platí

  \[ \mathrm{d}R\,=\,\frac{1}{\sigma}\,\frac{\mathrm{d}r}{2\pi r^2}\, , \]

  kde σ je elektrická vodivost země a 2πr² je povrch polokulové vrstvy.

  Celkový odpor poté určíme integrací přes všechny slupky, tj. od r₀ do nekonečna:

  \[ R\,=\,\int{\mathrm{d}R}\,=\,\int_\mathrm{r_0}^{\infty}{\frac{1}{\sigma}\,\frac{\mathrm{d}r}{2\pi r^2}}\,=\,\frac{1}{2\sigma\pi}\,\int_\mathrm{r_0}^{\infty}{\frac{\mathrm{d}r}{r^2}}\,=\, \frac{1}{2\sigma\pi}\,\left[-\,\frac{1}{r}\right]_\mathrm{r_0}^{\infty}\,=\,\frac{1}{2\sigma\pi\,r_0}\,. \]

  Celkový proud tekoucí do země určíme pomocí Ohmova zákona. Bude platit:

  \[ I\,=\,\frac{U}{R}\,=\,2U\sigma\pi r_0\,. \]

  Předpokládejme, že se tento proud roztéká do všech směrů země rovnoměrně. Pro proudovou hustotu ve vzdálenosti r od stožáru platí tedy vztah:

  \[ j\left(r\right)\,=\,\frac{I}{S}\,=\,\frac{I}{2\pi r^2}\,=\,\frac{\sigma U r_0}{r^2}\,. \]

  Užitím Ohmova zákona v diferenciálním tvaru určíme intenzitu elektrického pole ve vzdálenosti r od stožáru:

  \[ E\left(r\right)\,=\,\frac{j\left(r\right)}{\sigma}\,=\,\frac{Ur_0}{r^2}\, . \]

  Pro hledané napětí U_c poté platí vztah:

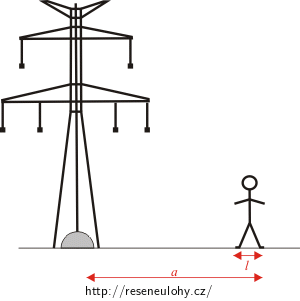
  \[ U_\mathrm{c}\,=\,\int_\mathrm{a-l}^\mathrm{a}{E\left(r\right)}\,\mathrm{d}r\,=\,\int_\mathrm{a-l}^\mathrm{a}{\frac{Ur_0}{r^2}}\,\mathrm{d}r\,=\,Ur_0\int_\mathrm{a-l}^\mathrm{a}\,{\frac{1}{r^2}}\,\mathrm{d}r\,, \]

  kde a značí vzdálenost člověka od stožáru a l je délka kroku, kterou člověk udělal směrem ke stožáru.

  

  Tedy:

  \[ U_\mathrm{c}\,=\,Ur_0\,\left[-\frac{1}{r}\right]_\mathrm{a-l}^\mathrm{a}\,=\,Ur_0\,\left(-\frac{1}{a}\,+\,\frac{1}{a-l}\right)=\frac{Ur_0l}{a\,\left(a-l\right)}\,. \]

• Číselné dosazení

  Ze zadání úlohy známe:

  U = 400 kV = 4·105 V	napětí elektrického stožáru
  r0 = 30 cm = 0,3 m	poloměr vodivé koule uzemňující elektrický stožár
  a = 100 m	vzdálenost člověka od elektrického stožáru
  l = 80 cm = 0,8 m	délka kroku, který člověk udělá směrem ke stožáru

  ---

  V minulém oddíle jsme získali vztah pro výpočet napětí, pod kterým se ocitne člověk, který udělá krok o délce l ve vzdálenosti a od stožáru směrem k němu:

  \[ U_1=\,=\,\frac{Ur_0l}{a\,\left(a-l\right)}\,=\,\frac{4{\cdot} 10^5{\cdot} 0{,}3{\cdot} 0{,}8}{100\cdot \left(100-0{,}8\right)}\,\mathrm{V}\,=\,9{,}7\,\mathrm{V}\,. \]

• Odpověď

  Člověk se ocitne pod napětím 9,7 V.

• Odkazy na podobné úlohy

  Zkuste si také vyřešit úlohy Elektrický proud mezi válcovými elektrodami, Nehomogenní prostředí mezi válcovými elektrodami a Měření vodivosti mořské vody.

• Komentář 1 – zjednodušující podmínky

  V této úloze samozřejmě pracujeme s mnoha zjednodušujícími podmínkami. Předpokládáme například, že země kolem elektrického stožáru je homogenní a proud se tedy do země roztéká rovnoměrně.

  Další idealizaci uvažujeme při výpočtu celkového odporu uzemnění. Vzorec, který jsme použili, a integrační meze od r₀ do nekonečna předpokládají, že Země je „rovná“ a „nekonečně velká“.

• Komentář 2 – chyba při přibližném výpočtu napětí

  Protože krok, který člověk udělá, je vzhledem ke vzdálenosti od stožáru malý, podívejme se, jaké chyby bychom se dopustili, kdybychom napětí vypočítali přibližně jako „krok krát intenzita“.

  Z řešení této úlohy víme, že intenzitu elektrického pole ve vzdálenosti a od stožáru vypočítáme ze vztahu:

  \[ E\left(a\right)\,=\,\frac{Ur_0}{a^2}\,, \]

  kde U je napětí na elektrickém stožáru a r₀ je poloměr vodivé koule uzemňující elektrický stožár.

  Napětí, pod kterým se vyskytne člověk, jestliže v této vzdálenosti udělá krok o délce l, vypočítáme jako součin elektrické intenzity pole ve vzdálenosti a od stožáru a délky kroku l:

  \[ U_{2}\,=\,\frac{Ur_0}{a^2}l. \]

  Hodnoty ze zadání úlohy:

  U = 400 kV = 4·105 V	napětí elektrického stožáru
  r0 = 30 cm = 0,3 m	poloměr vodivé koule uzemňující elektrický stožár
  a = 100 m	vzdálenost člověka od elektrického stožáru
  l = 80 cm = 0,8 m	délka kroku, který člověk udělá směrem ke stožáru

  Číselný výpočet:

  \[ U_2\,=\,\frac{4{\cdot} 10^5{\cdot} 0{,}3}{100^2}\cdot 0{,}8\,\mathrm{V}\,=\,9{,}6\,\mathrm{V}. \]

  Pokud tuto hodnotu porovnáme s hodnotou získanou v sekci Číselné dosazení, zjistíme, že chyba, které jsme se tímto výpočtem dopustili, činí jen 1 %.

  Se zkracující se vzdáleností člověka od stožáru se bude tato chyba zvětšovat.