Sbírka řešených úloh

Vliv měřicích přístrojů

Úloha číslo: 290

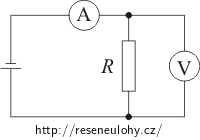
Pomocí voltmetru s vnitřním odporem 1,0 kΩ a ampérmetru s vnitřním odporem 2,0 Ω bylo naměřeno napětí na rezistoru R a proud protékající obvodem. Naměřené hodnoty jsou 12,4 V a 0,86 A. Jaká je velikost odporu rezistoru R s korekcí na vliv měřicích přístrojů? Jaké chyby se dopustíme, zanedbáme-li vliv měřicích přístrojů?

• Nápověda

  Co znamenají údaje, které ukazují voltmetr a ampérmetr? Jsou to skutečně hodnoty napětí a proudu platné pro samotný rezistor R?

• Řešení nápovědy

  Proud I_A, který ukazuje ampérmetr, je součtem proudů procházejících rezistorem I_R a voltmetrem I_V. Tedy:

  \[I_\mathrm{A}\,=\,I_\mathrm{R}\,+\,I_\mathrm{V}\,.\]

  Rezistor a voltmetr jsou zapojeny paralelně, a proto je na obou větvích obvodu stejné napětí. Voltmetr tedy ukazuje skutečnou hodnotu napětí na rezistoru:

  \[U_\mathrm{V}\,=\,U_\mathrm{R}.\]

• Rozbor

  

  Protože rezistor R a voltmetr jsou zapojeny paralelně, je na obou součástkách stejné napětí. Voltmetr tedy skutečně ukazuje, jaké je napětí na rezistoru R.

  Proud procházející ampérmetrem se v uzlu rozděluje na dvě části (do větve s voltmetrem a do větve s rezistorem R). Ampérmetr tedy měří součet proudů procházející rezistorem R a voltmetrem.

  Velikost odporu rezistoru R získáme pomocí Ohmova zákona jako podíl napětí na rezistoru a proudu, který rezistorem prochází. Již víme, že napětí na rezistoru je napětí, které jsme naměřili voltmetrem. Proud procházející rezistorem se rovná rozdílu celkového proudu obvodem (změřeného ampérmetrem) a proudu, který prochází voltmetrem. Proud protékající voltmetrem určíme také pomocí Ohmova zákona.

• Řešení

  

  Rezistor R a voltmetr jsou zapojeny paralelně. Na obou větvích je proto stejné napětí, jehož hodnotu ukazuje voltmetr:

  \[U_\mathrm{V}\,=\,U_\mathrm{R},\]

  kde U_V je napětí na voltmetru a U_R napětí na rezistoru R.

  Ampérmetr měří součet proudů rezistorem I_R a voltmetrem I_V. Tedy:

  \[I_\mathrm{A}\,=\,I_\mathrm{R}\,+\,I_\mathrm{V}.\]

  Pro odpor rezistoru podle Ohmova zákona platí:

  \[R\,=\,\frac{U_\mathrm{R}}{I_\mathrm{R}}\,=\,\frac{U_\mathrm{V}}{I_\mathrm{A}\,-\,I_\mathrm{V}}.\]

  Proud I_V procházející voltmetrem vypočítáme jako podíl napětí na voltmetru a odporu voltmetru:

  \[I_\mathrm{V}\,=\,\frac{U_\mathrm{V}}{R_\mathrm{V}}.\]

  Vztah pro výpočet odporu rezistoru je tedy:

  \[R\,=\,\frac{U_\mathrm{V}}{I_\mathrm{A}\,-\,\frac{U_\mathrm{V}}{R_\mathrm{V}}}.\]

• Číselné dosazení

  Ze zadání úlohy známe:

  RV = 1,0 kΩ = 1 000 Ω	vnitřní odpor voltmetru
  RA = 2,0 Ω	vnitřní odpor ampérmetru
  UV = 12,4 V	napětí na voltmetru
  IA = 0,86 A	proud ampérmetrem

  ---

  V minulém oddílu jsme získali vzorec pro výpočet odporu rezistoru R:

  \[R\,=\,\frac{U_\mathrm{V}}{I_\mathrm{A}\,-\,\frac{U_\mathrm{V}}{R_\mathrm{V}}}.\]

  Do tohoto vzorce dosadíme hodnoty ze zadání vzorce a číselně dopočítáme:

  \[R\,=\,\frac{12{,}4}{0{,}86\,-\,\frac{12{,}4}{1000}}\,\mathrm{\Omega}\,=\,14{,}6\,\mathrm{\Omega}.\]

  Pokud bychom do výpočtu nezahrnuli vliv měřicích přístrojů, pak odpor rezistoru R' získáme pomocí Ohmova zákona jako podíl napětí na rezistoru (hodnota změřená voltmetrem) a proudu, který rezistorem prochází (hodnota, kterou ukazuje ampérmetr):

  \[R'\,=\,\frac{U_\mathrm{V}}{I_\mathrm{A}}\,=\,\frac{12{,}4}{0{,}86}\,\mathrm{\Omega}\,=\,14{,}4\,\mathrm{\Omega}.\]

  Zanedbáním vlivu měřicích přístrojů jsme získali hodnotu o 0,21 Ω menší, než je skutečná hodnota odporu rezistoru R. Abychom získali relativní chybu měření, vydělíme rozdíl obou vypočítaných hodnot skutečnou hodnotou odporu a výsledek vynásobíme sty procenty:

  \[\frac{R-R_*}{R}\,\cdot 100\,\%\,=\,\frac{0{,}21\,\mathrm{\Omega}}{14{,}63\,\mathrm{\Omega}}\,\cdot 100\,\%\,=\,1{,}4\,\%.\]

  Chyba měření je tedy 1,4 %.

• Odpověď

  S korekcí na vliv měřicích přístrojů jsme zjistili, že odpor rezistoru R_x je 14,63 Ω.

  Pokud bychom korekce neuvažovali, dopustili bychom se chyby 1,4 %.

• Vnitřní odpory přístrojů ve skutečnosti

  V ideálním případě by ampérmetr neměl mít na obvod žádný vliv. Úbytek napětí, který na něm při průchodu proudu vzniká, by měl být co nejmenší. Proto musí mít ampérmetr co nejmenší vnitřní odpor. Reálné ampérmetry pro měření proudu v jednotkách ampérů mají vnitřní odpor desetiny až setiny ohmů. Se zvyšujícím se proudovým rozsahem ampérmetru klesá jeho vnitřní odpor.

  Aby voltmetr nezatěžoval obvod, musí jím procházet co nejmenší proud. Vnitřní odpor voltmetru musí být tedy co největší. Hodnoty vnitřních odporů voltmetrů, které měří v rozsahu desítek voltů, se řádově pohybují v desítkách až stovkách kiloohmů. Obecně platí, že se zvětšujícím se rozsahem přístroje roste i jeho vnitřní odpor.

  V této úloze jsou zadány vnitřní odpory „ne příliš dobrých“ přístrojů, proto chyba měření vyšla poměrně velká. Skutečné voltmetry mají odpor mnohem větší a ampérmetry naopak mnohem menší, a proto se při skutečném měření dopouštíme obvykle mnohem menší chyby.

  Použití zapojení

  Zapojení ampérmetru a voltmetru tak, jak je zobrazeno v zadání úlohy, se používá zejména při měření odporů mnohem menších, než je vnitřní odpor voltmetru.

  

  Odpor rezistoru R vypočítáme jako podíl napětí na rezistoru U (současně i napětí na voltmetru) a proudu I_R, který prochází rezistorem:

  \[ R\,=\,\frac{U}{I_\mathrm{R}}. \]

  Proud I_R procházející rezistorem si můžeme vyjádřit jako rozdíl proudu I_A, který prochází ampérmetrem, a proudu I_V procházejícího voltmetrem:

  \[I_\mathrm{R}\,=\,I_\mathrm{A}-I_\mathrm{V}.\]

  Proud I_V, který protéká voltmetrem, se rovná podílu napětí U na voltmetru a vnitřního odporu voltmetru R_V:

  \[I_\mathrm{V}\,=\,\frac{U}{R_\mathrm{V}}.\]

  Pro výpočet odporu rezistoru tedy platí:

  \[ R\,=\,\frac{U}{I_\mathrm{R}}\,=\,\frac{U}{I_\mathrm{A}-I_\mathrm{V}}\,=\,\frac{U}{I_\mathrm{A}-\frac{U}{R_\mathrm{V}}} \] \[ R_\mathrm{V}\,>>\,R\hspace{20px}\Rightarrow\hspace{20px}R\,=\,\frac{U}{I_A}. \]

  Toto zapojení není vhodné pro rezistory s vysokým odporem. Pokud bychom do tohoto obvodu zapojili rezistor, jehož odpor by byl srovnatelný s vnitřním odporem voltmetru, pak při zanedbání měřicích přístrojů bychom se při výpočtu dopustili značné chyby.

  Jiné zapojení měřicích přístrojů

  Existuje ještě další způsob zapojení měřicích přístrojů, který je znázorněn na obrázku.

  

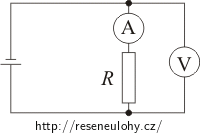
  Protože v tomto obvodu jsou ampérmetr a rezistor připojeny sériově, prochází jimi stejný proud (a ampérmetr tedy skutečně ukazuje proud procházející rezistorem). Nyní ale voltmetr ukazuje součet napětí na rezistoru a na ampérmetru. Proto při tomto zapojení musíme počítat s vlivem voltmetru.

  Toto zapojení je vhodné zvláště pro měření odporů, které jsou mnohem větší, než je vnitřní odpor použitého ampérmetru, neboť platí:

  \[U_\mathrm{V}\,=\,R_\mathrm{A}I\,+\,RI,\]

  kde U_V je napětí na voltmetru (tuto hodnotu voltmetr ukazuje), R_A je vnitřní odpor ampérmetru, R je odpor rezistoru a I je proud procházející ampérmetrem a rezistorem.

  Tedy:

  \[R\,=\,\frac{U_\mathrm{V}}{I}\,-\,R_\mathrm{A}\] \[R\,>>\,R_\mathrm{A}\hspace{20px}\Rightarrow\hspace{20px}R\,=\,\frac{U_\mathrm{V}}{I}.\]

  Toto zapojení není vhodné pro rezistory, jejichž odpor je srovnatelný s vnitřním odporem ampérmetru. V takovém případě by totiž při zanedbání vnitřních odporů měřicích přístrojů byla naše měření velmi nepřesná.