Teplo uvolněné ve vodiči
Úloha číslo: 804
Vodičem o odporu 6 Ω prošel náboj 30 C. Určete teplo, které se uvolnilo ve vodiči v těchto případech:
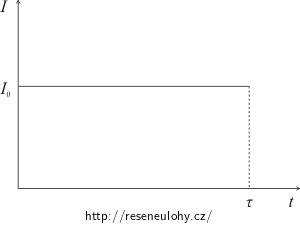
a) proud byl konstantní a protékal po dobu 24 s,
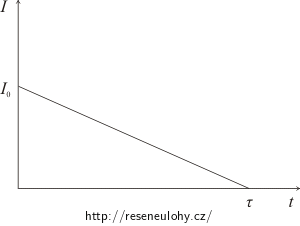
b) proud rovnoměrně klesal až na nulu po dobu 24 s,
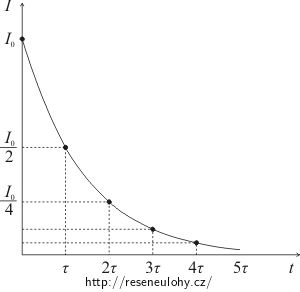
c) proud exponenciálně klesal tak, že za každých 24 s klesl na polovinu předchozí hodnoty,
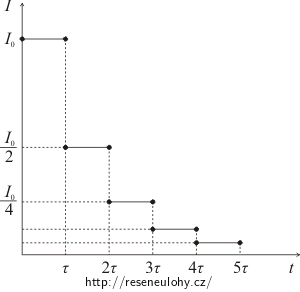
d) proud stupňovitě klesal tak, že za každých 24 s klesl na polovinu předchozí hodnoty.
Nápověda 1
Uvědomte si nebo vyhledejte, jak lze vypočít teplo, které se uvolní ve vodiči při průchodu elektrického proudu.
Nápověda 2
Uvědomte si, jak vypadají průběhy proudů v závislosti na čase v jednotlivých případech. Zkuste tyto závislosti matematicky vyjádřit.
Rozbor
Teplo, které vzniká ve vodiči průchodem elektrického proudu, se nazývá Jouleovo teplo. To závisí na odporu vodiče, proudu, který vodičem protéká, a čase, po který proud vodičem protéká.
V případě, že vodičem neprotéká konstantní proud, musíme najít matematický vztah pro časovou závislost proudu a velikost Jouleova tepla zintegrovat přes zadaný časový interval.
Řešení části a): proud je konstantní
Podle Jouleova–Lenzova zákona je teplo uvolněné ve vodiči o odporu R protékaném stálým proudem I za dobu τ dáno vztahem:
\[W\,=\,RI^2\tau\,.\]Je-li proud v obvodu konstantní, platí pro celkový prošlý náboj Q:
\[Q\,=\,I\tau,\]tedy:
\[I\,=\,\frac{Q}{\tau}\,.\]Po dosazení tohoto vztahu do rovnice pro výpočet uvolněného tepla dostáváme:
\[W\,=\,R\frac{Q^2}{\tau^2}\tau\,=\,R\frac{Q^2}{\tau}\,.\]Řešení části b): proud rovnoměrně klesá
Tentokrát je situace komplikovanější v tom, že proud již není konstantní, ale mění se s ubíhajícím časem. V takovém případě musíme pro výpočet tepla uvolněného ve vodiči v době od 0 do τ použít obecnější vzorec:
\[ W\,=\,\int_0^{\tau}RI^2\left(t\right)\mathrm{d}t\,. \]Naším úkolem je tedy nalezení funkční závislosti proudu tekoucího vodičem na čase. Jestliže proud klesá rovnoměrně, je hledaná závislost lineární, a lze ji tedy zapsat ve tvaru:
\[ I\,=\,I_0\,+\,kt\,, \]kde I0 a k jsou konstanty, jež musíme určit. (Pozn.: Zde bude mít konstanta I0 jinou hodnou než v části a).)
Je jasné, že I0 udává proud tekoucí vodičem v čase t = 0 s. Vzhledem k tomu, že proud klesal rovnoměrně, prošel vodičem stejný náboj, jako by prošel při konstantním proudu o poloviční velikosti v porovnání s počátečním proudem I0. Pro tento počáteční proud proto platí vztah:
\[ Q = \frac{I_0}{2}\tau \qquad \Rightarrow \qquad I_0=\frac{2Q}{\tau}\,. \]Konstantu k určíme z faktu, že v čase τ byl proud roven nule:
\[ 0=I_0\,+\,k\tau \qquad \Rightarrow \qquad k=-\frac{I_0}{\tau}=-\frac{2Q}{{\tau}^2}\,. \]Dosazením do výše uvedeného obecného vzorce pro výpočet tepla uvolněného ve vodiči dostáváme:
\[ W=\int_0^{\tau}RI^2\left(t\right)\mathrm{d}t =R\int_0^{\tau}\left(\frac{2Q}{\tau}-\frac{2Q}{\tau^2}t\right)^2\mathrm{d}t=R\int_0^{\tau}\left(4\frac{Q^2}{\tau^2}-8\frac{Q^2}{\tau^3}t+4\frac{Q^2}{\tau^4}t^2\right)\mathrm{d}t= \] \[ =4R\frac{Q^2}{\tau^2}\,\left(\int_0^{\tau}\mathrm{d}t\,-\,\int_0^{\tau}\frac{2t}{\tau}\mathrm{d}t\,+\,\int_0^{\tau}\frac{t^2}{\tau^2}\,\mathrm{d}t\right)=4R\frac{Q^2}{\tau^2}\,\left(\tau\,-\,\tau\,+\,\frac{1}{3}\tau\right)\,. \]Výsledný vzorec pro výpočet tepla tedy je:
\[ W\,=\,\frac{4}{3}\,\frac{RQ^2}{\tau}\,. \]Řešení části c): proud exponenciálně klesá
Stejně jako v předchozí části úlohy budeme muset k výpočtu uvolněného tepla použít obecnější integrální vzorec. Rozdíl bude v složitější (nelineární) závislosti proudu na čase a také v integračních mezích u zmíněného vzorce. Musíme si totiž uvědomit, že při exponenciálním poklesu se proud sice s běžícím časem bude k nule nekonečně přibližovat, ale nikdy jí nedosáhne. Proto musíme za horní integrační mez položit nekonečno a pracovat s nevlastním integrálem. Pro uvolněné teplo tedy platí vztah:
\[ W\,=\,\int_0^{\infty}RI^2\left(t\right)\mathrm{d}t\,. \]Naším prvním úkolem bude nalezení funkční závislosti celkového náboje ještě neprošlého vodičem na čase. Skutečnost, že proud klesá exponenciálně tak, že vždy po určité době poklesne na polovinu předchozí hodnoty, totiž můžeme interpretovat tak, že procházející proud je přímo úměrný náboji, který ještě neprošel vodičem. Protože elektrický proud není nic jiného než časová změna náboje, získáváme pro náboj diferenciální rovnici:
\[ \frac{\mathrm{d}Q}{\mathrm{d}t}\,=\,-\,kQ\,. \]Jejím řešením, jež provedeme separací proměnných, obdržíme vztah:
\[Q\,=\,c\cdot e^\mathrm{-kt}\,.\]Konstanty c a k musíme určit z okrajových podmínek. Především víme, že v čase t = 0 s je náboj Q roven celkovému náboji, což je Q0. Proto můžeme psát uvedenou funkční závislost neprošlého náboje na čase ve tvaru:
\[Q\,=\,Q_0\cdot e^\mathrm{-kt}\,.\]Konstantu k určíme z toho, že za dobu τ = 24 s poklesne proud, a tudíž i neprošlý náboj, na polovinu. Proto musí v souladu s vyvozenou funkční závislostí platit vztah:
\[ \frac{Q_0}{2}\,=\,Q_0\cdot e^\mathrm{-k\tau}\hspace{5px}\rightarrow\hspace{5px}\frac{1}{2}\,=\,e^\mathrm{-k\tau}\hspace{5px}\rightarrow\hspace{5px}k\,=\,\frac{\ln{2}}{\tau}\,. \]Díky tomu můžeme psát:
\[Q\,=\,Q_0\cdot e^{-\frac{\ln{2}}{\tau}t}.\]Pro funkční závislost proudu protékajícího vodičem na čase pak dostáváme:
\[ I\,=\,-\,\frac{\mathrm{d}Q}{\mathrm{d}t}\,=\,Q_0\,\frac{\ln{2}}{\tau}\,e^{-\frac{\ln{2}}{\tau}t}. \]Nyní již můžeme dosadit do obecného vzorce pro výpočet tepla uvolněného ve vodiči:
\[ W\,=\,\int_0^{\infty}RI^2\left(t\right)\mathrm{d}t\,=\,R\int_0^{\infty}\left(Q_0\,\frac{\ln{2}}{\tau}\,e^{-\frac{\ln{2}}{\tau}t}\right)^2\mathrm{d}t\,= \] \[ =\,RQ_0^2\,\frac{\ln^2{2}}{\tau^2}\int_0^{\infty}e^{-2\frac{\ln{2}}{\tau}t}\mathrm{d}t\,=\,-\frac{1}{2}RQ_0^2\,\frac{\ln{2}}{\tau}\int_0^{-\infty}e^u\mathrm{d}u\,=\,-\frac{1}{2}RQ_0^2\,\frac{\ln{2}}{\tau}\,\cdot\,\left(-1\right)\,. \]
Poznámka:
Při integraci jsme použili substituci \(u\,=\,-2\,\frac{\ln{2}}{\tau}t,\hspace{5px}\mathrm{d}u\,=\,-2\,\frac{\ln{2}}{\tau}\mathrm{d}t.\)
Výsledný vzorec pro výpočet tepla:
\[ W\,=\,\frac{1}{2}RQ_0^2\,\frac{\ln{2}}{\tau}\,. \]Řešení části d): proud stupňovitě klesá
Při řešení této části úlohy využijeme faktu, že proud protékající vodičem je po částech konstantní. Označíme-li si proud tekoucí vodičem po dobu prvních 24 sekund I0, můžeme s využitím skutečnosti, že proud po 24 sekundách vždy klesá na polovinu předchozí hodnoty, pro celkové teplo uvolněné ve vodiči psát:
\[ W=W_1+W_2+W_3+\,...=RI_0^2\tau+R\left(\frac{I_0}{2}\right)^2\tau+R\left(\frac{I_0}{4}\right)^2\tau+\,... \] \[ W=RI_0^2\,\tau\,\left(1+\frac{1}{4}+\frac{1}{16}+\,...\right)\,. \]Při další úpravě využijeme skutečnost, že výraz v závorce je geometrickou řadou s počátečním členem 1 a kvocientem \(\frac{1}{4}\):
\[ W=RI_0^2\,\tau\sum_{n=0}^{\infty}{\frac{1}{4^n}}\,=\,RI_0^2\,\tau\,\frac{1}{1-\frac{1}{4}}\,=\,\frac{4}{3}RI_0^2\,\tau\,. \]Nyní musíme určit proud I0. Pro celkový náboj prošlý vodičem, jehož velikost máme zadanou, bude platit:
\[ Q=Q_1+Q_2+Q_3+\,...=I_0\,\tau+\frac{1}{2}I_0\,\tau+\frac{1}{4}I_0\,\tau+\,... \] \[ Q=I_0\,\tau\left(1+\frac{1}{2}+\frac{1}{4}+\,...\right)=I_0\,\tau\sum_{n=0}^{\infty}{\frac{1}{2^n}} \] \[ Q=I_0\,\tau\,\frac{1}{1-\frac{1}{2}}\,=\,2I_0\,\tau\,. \]Pro proud I0 dostáváme:
\[ I_0\,=\,\frac{Q}{2\tau}\,. \]Dosazením do výše odvozeného vztahu pro celkové teplo uvolněné ve vodiči poté získáváme:
\[ W=\frac{4}{3}RI_0^2\,\tau=\,\frac{4}{3}R\,\frac{Q^2}{4\tau^2}\,\tau \] \[ W=\frac{RQ^2}{3\tau}\,. \]Číselné dosazení
Ze zadání úlohy známe:
R = 6 Ω odpor vodiče Q = 30 C celkový náboj prošlý vodičem
Ze vztahů, které jsme získali v minulých oddílech (Řešení části a) – d)), určíme teplo W, které se uvolnilo ve vodiči, jestliže
a) proud byl konstantní a protékal po dobu τ = 24 s:
\[ W=R\frac{Q^2}{\tau}=6\cdot\frac{30^2}{24}\,\mathrm{J}=225\,\mathrm{J}\,; \]b) proud rovnoměrně klesal až na nulu po dobu τ = 24 s:
\[ W=\frac{4}{3}\,\frac{RQ^2}{\tau}=\frac{4}{3}\cdot\frac{6{\cdot} 30^2}{24}\,\mathrm{s}=300\,\mathrm{J}\,; \]c) proud exponenciálně klesal tak, že za každých τ = 24 s klesl na polovinu předchozí hodnoty:
\[ W=\frac{1}{2}\,RQ^2\,\frac{\ln{2}}{\tau}=\frac{1}{2}\cdot6{\cdot} 30^2\cdot\frac{\ln{2}}{24}\,\mathrm{J}\,\dot{=}\,78\,\mathrm{J}\,; \]d) proud stupňovitě klesal tak, že za každých τ = 24 s klesl na polovinu předchozí hodnoty:
\[ W=\frac{RQ^2}{3\tau}=\frac{6{\cdot}30^2}{3{\cdot}24}\,\mathrm{J}=75\,\mathrm{J}\,. \]Odpověď
a) Z vodiče, kterým po dobu 24 s protéká konstantní proud, se uvolní teplo 225 J.
b) Jestliže proud procházející vodičem rovnoměrně klesá po dobu 24 s až na nulu, pak se z vodiče uvolní teplo 300 J.
c) Teplo, které se uvolní z vodiče v případě, že proud exponenciálně klesá tak, že za každých 24 s klesne na polovinu předchozí hodnoty, je 78 J.
d) Pokud proud procházející vodičem stupňovitě klesá tak, že za každých 24 s klesne na polovinu předchozí hodnoty, pak se z vodiče uvolní teplo 75 J.