Sbírka řešených úloh

Výkon elektrického motoru

Úloha číslo: 163

• Zápis

  Ze zadání známe:

  Napětí zdroje:	Uef = 230 V
  Frekvence zdroje:	f = 50 Hz
  Výstupní výkon:	P = 74,6 W
  Efektivní proud:	Ief = 0,65 A

  Chceme určit:

  Odpor motoru: R = ? (Ω)

• Nápověda 1

  Použijeme vzorec pro výpočet výkonu v obvodu se střídavým proudem, který obsahuje také fázové posunutí mezi napětím a proudem.

• Nápověda 2

  Elektrický motor si můžeme představit jako spojení rezistoru a cívky.

• Rozbor

  Protože motorem protéká střídavý proud, musíme při výpočtu výkonu vzít v úvahu i fázové posunutí mezi napětím a proudem. Ve vzorci pro výkon vystupuje kosinus fázového posunutí, tzv. účiník.

  Ze zadaného proudu protékajícího motorem, napětí zdroje a výkonu motoru zjistíme fázové posunutí mezi napětím a proudem. Pomocí Ohmova zákona určíme celkovou impedanci a z fázového posunutí potom zjistíme hodnotu odporu.

• Řešení

  Výkon elektrického motoru v obvodu se střídavým proudem je dán vztahem

  \[P=I_{\mathrm{ef}} U_{\mathrm{ef}} \cos \varphi.\]

  Vyjádříme si kosinus fázového posunu:

  \[\cos\varphi= \frac{P}{I_{\mathrm{ef}}U_{\mathrm{ef}}}. \]

  Pomocí Ohmova zákona vyjádříme velikost celkové impedance motoru Z:

  \[Z= \frac{U_{\mathrm{ef}}}{I_{\mathrm{ef}}}.\]

  Nakreslíme si fázorový diagram, do kterého zaneseme již známé hodnoty fázového posunutí a impedance. Velikost odporu vyjádříme ze vzniklého trojúhelníku.

  

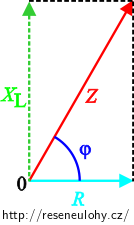
  Vidíme, že

  \[R=Z \cos\varphi.\]

  Dosadíme za kosinus fázového posunutí a impedanci:

  \[R= \frac{U_{\mathrm{ef}}}{I_{\mathrm{ef}}}\, \frac{P}{I_{\mathrm{ef}} U_{\mathrm{ef}}}= \frac{P}{(I_{\mathrm{ef}})^2}. \]

  ---

  Číselné dosazení:

  Fázové posunutí:

  \[\cos \varphi= \frac{74{,}6}{0{,}65{\cdot} 230}\,\dot{=}\,0{,}5 \] \[ \varphi \,\dot{=}\,\frac{\pi}{3} \]

  Celková impedance motoru:

  \[Z= \frac{230}{0{,}65}\,\mathrm \Omega\,\dot{=}\,353{,}8\,\mathrm \Omega \,\dot{=}\,350\,\mathrm \Omega\]

  Odpor motoru:

  \[R=\frac{P}{(I_{\mathrm{ef}})^2} = \frac{74{,}6}{0{,}65^2} \,\mathrm \Omega \,\dot{=}\, 177\,\mathrm \Omega \,\dot{=}\, 180\,\mathrm \Omega \]

• Odpověď

  Elektrický motor připojený ke zdroji střídavého napětí, který koná práci s výstupním výkonem 74,6 W, má odpor přibližně R = 180 Ω.

• Komentář: Indukčnost elektrického motoru

  Vzhledem k tomu, že motor obsahuje cívky, můžeme předpokládat, že fázové posunutí mezi napětím a proudem je způsobeno spíše indukčností motoru než kapacitou motoru.

  Indukčnost elektrického motoru vypočteme také z fázorového diagramu:

  \[X_\mathrm{L}=Z\sin\varphi,\] \[2 \pi f L=Z\sin\varphi,\] \[L=\frac{Z\sin\varphi}{2 \pi f}.\]

  ---

  Dosadíme číselně:

  \[ L\dot=\frac{353{,}8 \cdot \sin \left(\dfrac{\pi}{3}\right)}{2 \pi \cdot 50}\, \mathrm H\,\dot{=}\,0{,}98\,\mathrm H\]