RLC obvod se svorkami
Úloha číslo: 174
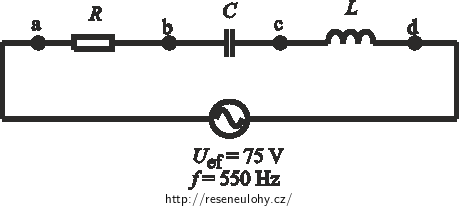
Na obrázku je sériový RLC obvod, ve kterém je odpor rezistoru 15 Ω, kapacita kondenzátoru je 4,7 μF a indukčnost cívky je 25 mH. Generátor dodává efektivní napětí 75 V při frekvenci 550 Hz.
Zápis
Ze zadání známe:
Odpor rezistoru: R = 15 Ω Kapacitu kondenzátoru: C = 4,7 μF Indukčnost cívky: L = 25 mH Napětí zdroje: Uef = 75 V Frekvenci napětí zdroje: f = 550 Hz Chceme určit:
a) Efektivní proud: Ief = ? (A) b) Efektivní napětí mezi svorkami ab: Uab = ? (V) Efektivní napětí mezi svorkami bc: Ubc = ? (V) Efektivní napětí mezi svorkami cd: Ucd = ? (V) Efektivní napětí mezi svorkami bd: Ubd = ? (V) Efektivní napětí mezi svorkami ad: Uad = ? (V) c) Ztrátový výkon v rezistoru: PR = ? (W) Ztrátový výkon v cívce: PL = ? (W) Ztrátový výkon v kondenzátoru: PC = ? (W) Nápověda 1
Použijeme Ohmův zákon pro střídavý proud a vzorec pro výpočet výkonu v obvodu se střídavým proudem, ve kterém dochází k fázovému posunu mezi napětím a proudem.
Nápověda 2
Napětím Uab v zadání jsme označili napětí mezi svorkami ab v obvodu. To samé platí pro ostatní napětí.
Rozbor
a) Efektivní proud v obvodu získáme pomocí Ohmova zákona. Známe efektivní napětí zdroje a celkovou impedanci vypočteme z induktance, rezistance a kapacitance jednotlivých prvků v obvodu.
b) Jednotlivá efektivní napětí vypočteme také pomocí Ohmova zákona. Protože se jedná o sériový obvod, protéká všemi prvky stejný proud. Tento efektivní proud protékající obvodem jsme si vypočítali v oddíle a). Impedance do Ohmova zákona vyjádříme vždy pomocí těch součástek, které jsou zařazeny mezi danými dvěma svorkami.
c) Pro výpočet výkonu na jednotlivých součástkách použijeme vzorec pro výkon v obvodu se střídavým proudem. Ve vyjádření výkonu vystupuje jak efektivní napětí a efektivní proud, tak fázový posun mezi napětím na dané součástce a proudem.
a) Řešení
Efektivní proud vyjádříme pomocí Ohmova zákona:
\[I_\mathrm{ef}=\frac{U_\mathrm{ef}}{Z}=\frac{U_\mathrm{ef}}{\sqrt{R^2+\left(X_\mathrm{L}-X_\mathrm{C}\right)^2}}=\frac{U_\mathrm{ef}}{\sqrt{R^2+\left(2 \pi f L-\frac{1}{2 \pi f C}\right)^2}}.\]
Číselné dosazení:
\[I_\mathrm{ef}=\frac{75}{\sqrt{15^2+\left(2\pi \cdot 550 {\cdot} 0{,}025-\frac{1}{2 \pi \cdot 550 {\cdot} 4{,}7 {\cdot} 10^{-6}}\right)^2}}\,\mathrm A \,\dot{=}\,2{,}6\,\mathrm A\]b) Řešení
Dílčí efektivní napětí vypočteme z Ohmova zákona. Protože se jedná o sériový obvod, všemi součástkami protéká stejně velký proud, který jsme vypočítali v oddíle a).
Efektivní napětí Uab, zapojen rezistor:
\[U_\mathrm{ab}=I_{\mathrm{ef}}\,Z_{\mathrm{ab}}=I_{\mathrm{ef}}\,R.\]Efektivní napětí Ubc, zapojen kondenzátor:
\[U_\mathrm{bc}=I_{\mathrm{ef}}\,Z_{bc}=I_{\mathrm{ef}}\,X_\mathrm{C}=I_{\mathrm{ef}}\,\frac{1}{2 \pi f C}.\]Efektivní napětí Ucd, zapojena cívka:
\[U_{\mathrm{cd}}=I_{\mathrm{ef}}\,Z_{\mathrm{cd}}=I_{\mathrm{ef}}\,X_\mathrm{L}=I_{\mathrm{ef}}\, 2 \pi f L.\]Efektivní napětí Ubd, zapojena cívka a kondenzátor:
\[U_{\mathrm{\mathrm{bc}}}=I_{\mathrm{ef}}\,Z_{\mathrm{\mathrm{bc}}}=I_{\mathrm{ef}}\, \left|X_\mathrm{L}-X_\mathrm{C}\right|=I_{\mathrm{ef}}\,\left| 2 \pi f L-\frac{1}{2 \pi f C}\right|.\]Efektivní napětí Uad, zapojena cívka, kondenzátor a rezistor:
\[U_{\mathrm{ad}}=I_{\mathrm{ef}}\,Z_{\mathrm{ad}}=I_{\mathrm{ef}}\,\sqrt{R^2+\left(X_\mathrm{L}-X_\mathrm{C}\right)^2}=I_{\mathrm{ef}}\, \sqrt{R^2+\left(2 \pi f L-\frac{1}{2 \pi f C}\right)^2}.\]Napětí Uad je napětí na všech prvcích v obvodu, to znamená, že se musí rovnat efektivnímu napětí, které je dodáváno ze zdroje. Ověříme si to dosazením obecného vyjádření efektivního proudu v obvodu, který jsme si vypočítali v oddíle a):
\[U_{\mathrm{ad}}=I_{\mathrm{ef}}\,\sqrt{R^2+\left(X_\mathrm{L}-X_\mathrm{C}\right)^2}=\frac{U_{\mathrm{ef}}\,\sqrt{R^2+\left(X_\mathrm{L}-X_\mathrm{C}\right)^2}}{\sqrt{R^2+\left(X_\mathrm{L}-X_\mathrm{C}\right)^2}},\] \[U_{\mathrm{ad}}=U_{\mathrm{ef}}.\]
Číselné řešení:
\[U_{\mathrm{ab}}=2{,}6 {\cdot} 15 \,\mathrm V\,\dot{=}\,40\,\mathrm V\] \[U_\mathrm{bc}=2{,}6\cdot \frac{1}{2\pi \cdot 550 {\cdot} 4{,}7 {\cdot} 10^{-6} } \,\mathrm{V}\,\dot{=}\,160\,\mathrm{V}\] \[U_{\mathrm{cd}}=2{,}6{\cdot} 2\pi \cdot 550 {\cdot} 25 \cdot 10^{-3} \,\mathrm{V}\,\dot{=}\, 220\,\mathrm V\] \[U_{\mathrm{\mathrm{bd}}}=2{,}6\cdot \left|2\pi \cdot 550 {\cdot} 25 \cdot 10^{-3}-\frac{1}{2\pi \cdot 550 {\cdot} 4{,}7 {\cdot} 10^{-6}}\right| \,\mathrm{ V}\,\dot{=}\,64\,\mathrm V\] \[U_{\mathrm{ad}}=75\,\mathrm V\]c) Řešení
Pro střední hodnotu výkonu v obvodu se střídavým proudem platí:
\[P=U_{\mathrm{ef}}\, I_{\mathrm{ef}}\, \cos\varphi\mathrm{,}\]kde φ je fázový posun mezi napětím a proudem.
Výkon na rezistoru:
\[P_\mathrm{R}=U_\mathrm{R}\,I_{\mathrm{ef}}\,\cos{\varphi}_\mathrm{R}=U_{\mathrm{ab}}\,I_{\mathrm{ef}}\,\cos{\varphi}_\mathrm{R}\mathrm{,}\]kde fázový posun mezi napětím a proudem φR je nulový.
\[P_\mathrm{R}=40{\cdot} 2{,}6\cdot \cos\,0\,\mathrm W\,\dot{=}\,100\,\mathrm W\]Výkon na kondenzátoru:
\[P_\mathrm{C}=U_\mathrm{C}\,I_{\mathrm{ef}}\,\cos{\varphi}_\mathrm{R}=U_\mathrm{bc}\,I_{\mathrm{ef}}\,\cos{\varphi}_\mathrm{C}\mathrm{,}\]kde fázový posun mezi napětím a proudem φC je π/2.
\[P_\mathrm{C}=160{\cdot} 2{,}6\cdot \cos\left(\frac{\pi}{2}\right)\,\mathrm W=0\,\mathrm W\]To, že má střední hodnota výkonu na kondenzátoru nulovou velikost, je způsobeno tím, že se kondenzátor stále vybíjí a nabíjí. Elektrická energie se do něj ukládá a hned zase odebírá.
Výkon na cívce:
\[P_\mathrm{L}=U_\mathrm{L}\,I_{\mathrm{ef}}\,\cos{\varphi}_\mathrm{R}=U_{\mathrm{cd}}\,I_{\mathrm{ef}}\,\cos{\varphi}_\mathrm{L}\mathrm{,}\]kde fázový posun mezi napětím a proudem φL je -π/2.
\[P_\mathrm{L}=220{\cdot} 2{,}6\cdot \cos\left(-\frac{\pi}{2}\right)\,\mathrm W=0\,\mathrm W\]Střední hodnota výkonu na cívce má nulovou velikost, protože se energie uvnitř cívky mění na energii magnetického pole a zase zpět na elektrickou energii.
Odpověď
Efektivní proud protékající obvodem má hodnotu asi 2,6 A.
Jednotlivá napětí mezi svorkami zakreslenými ve schématu zapojení jsou přibližně: Uab = 40 V; Ubc = 160 V; Ucd = 220 V; Ubd = 64 V a Uad = 75 V.
Výkon elektrického proudu na rezistoru má hodnotu asi 100 W, výkon na cívce i kondenzátoru je nulový.


