Kulový kondenzátor
Úloha číslo: 492
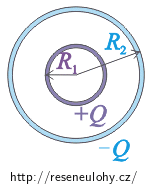
Kulový kondenzátor tvoří dvě soustředné vodivé kulové slupky o poloměrech R1 a R2, kde R1 < R2.
a) Určete kapacitu kondenzátoru.
b) Určete kapacitní a influenční koeficienty.
a) Nápověda: Kapacita
Představme si, že kondenzátor nabijeme nábojem Q. Mezi nábojem, napětím na kondenzátoru a kapacitou kondenzátoru platí vztah:
\[C\,=\,\frac{Q}{U}\,.\]Abychom mohli vyjádřit kapacitu kondenzátoru, musíme určit, jaké je napětí mezi deskami.
Uvědomte si, jak souvisí napětí mezi elektrodami, tj. kulovými vrstvami kondenzátoru, s potenciálem a intenzitou elektrického pole mezi nimi.
a) Nápověda: Intenzita pole mezi kulovými vrstvami
Využijte výsledek úlohy Pole rovnoměrně nabité sféry, kde je vypočítaná intenzita v okolí tenké kulové vrstvy.
a) Rozbor
Kulový kondenzátor tvoří dvě soustředné kulové slupky, které jsou nabity stejně velkým nábojem opačného znaménka.
Kapacitu kondenzátoru můžeme určit jako poměr náboje a napětí mezi kulovými vrstvami kondenzátoru.
Napětí mezi kulovými vrstvami, tedy rozdíl potenciálů na elektrodách, bude rovno integrálu intenzity podél spojnice obou elektrod. (Podrobnější vysvětlení naleznete v první nápovědě.)
Intenzita vně nabité kulové vrstvy klesá s druhou mocninou vzdálenosti od středu kulové vrstvy a uvnitř vrstvy je rovna nule (viz úloha Pole rovnoměrně nabité sféry). Mezi kulovými vrstvami tedy intenzita klesá s druhou mocninou vzdálenosti od středu kulových vrstev. Vnější kulová vrstva k intenzitě elektrického pole nepřispívá.
a) Řešení: Kapacita kondenzátoru
Kapacitu C kulového kondenzátoru určíme jako podíl náboje Q na elektrodách a napětí U mezi nimi:
\[C\,=\,\frac{Q}{U}\,.\]Velikost napětí mezi elektrodami je rovna integrálu z intenzity (podrobnější vysvětlení naleznete v nápovědě):
\[U\,=\, \int_\mathrm{R_1}^\mathrm{R_2} E \,\mathrm{d}z\,,\]kde z je vzdálenost od středu obou kulových vrstev.
Intenzita elektrického pole mezi kulovými vrstvami je dána intenzitou elektrického pole vnitřní vrstvy. Vnější kulová vrstva k intenzitě elektrického pole mezi elektrodami nepřispívá. Intenzitu elektrického pole v okolí nabité kulové vrstvy jsme vyjádřili v úloze Pole rovnoměrně nabité sféry pomocí vztahu
\[E\,=\,\frac{R_1^2 \sigma}{\epsilon_0} \,\frac{1}{z^2}\,,\]kde poloměr kulové vrstvy je roven R1. Dosadíme do vztahu pro napětí:
\[U\,=\, \int_\mathrm{R_1}^\mathrm{R_2} \frac{R_1^2 \sigma}{\epsilon_0} \,\frac{1}{z^2}\,\mathrm{d}z\,.\]Vytkneme konstanty před integrál a integrál vypočítáme:
\[U\,=\, \frac{R_1^2 \sigma}{\epsilon_0} \int_\mathrm{R_1}^\mathrm{R_2} \frac{1}{z^2}\,\mathrm{d}z \,=\, \frac{R_1^2 \sigma}{\epsilon_0} \,\left[-\frac{1}{z}\right]_\mathrm{R_1}^\mathrm{R_2} \,=\, \frac{R_1^2 \sigma}{\epsilon_0} \,\left(-\,\frac{1}{R_2}\,+\,\frac{1}{R_1}\right),\] \[U\,=\, \frac{R_1^2 \sigma}{\epsilon_0} \,\left(\frac{1}{R_1}\,-\,\frac{1}{R_2}\right).\tag{+}\]Protože neznáme plošnou nábojovou hustotu σ, ale celkový náboj Q, vyjádříme σ pomocí povrchu kulové vrstvy:
\[Q\,=\, \sigma S\,=\, \sigma \,4 \pi R_1^2 \hspace{40px} \Rightarrow \hspace{40px}\sigma\,=\,\frac{Q}{4 \pi R_1^2}.\]Nábojovou hustotu σ dosadíme zpět do vzorce (+) a výraz upravíme:
\[U\,=\, \frac{R_1^2}{\epsilon_0}\,\,\frac{Q}{4 \pi R_1^2} \,\,\left(\frac{1}{R_1}\,-\,\frac{1}{R_2}\right)\,=\,\frac{Q}{4 \pi \epsilon_0} \,\left(\frac{1}{R_1}\,-\,\frac{1}{R_2}\right).\]Výraz v závorce ještě převedeme na společného jmenovatele:
\[U\,=\,\frac{Q}{4 \pi \epsilon_0} \,\frac{R_2\,-\,R_1}{R_1 R_2}.\]Protože kapacita C kondenzátoru je dána podílem \(C\,=\,\frac{Q}{U}\), můžeme ji z posledního vzorce vyjádřit:
\[C\,=\,4 \pi \epsilon_0\,\frac{R_1 R_2}{R_2\,-\,R_1}. \]b) Nápověda: Jak vyjádřit kapacitní a influenční koeficienty
Jestliže je vnitřní (první) kulová slupka nabita nábojem Q1 a vnější (druhá) slupka nabita nábojem Q2, můžeme kapacitní a influenční koeficienty vyjádřit z těchto rovnic:
\[Q_1\,=\,C_{11}\varphi_{1}\,+\,C_{12}\varphi_{2}\,,\] \[Q_2\,=\,C_{21}\varphi_{1}\,+\,C_{22}\varphi_{2}\,,\tag{*}\]kde φ1 je potenciál na vnitřní (první) slupce a φ2 je potenciál na vnější (druhé) slupce.
Koeficienty C11 a C22 se nazývají kapacitní. Koeficienty C12 a C21 se nazývají influenční.
Protože elektrody kondenzátoru jsou vodivé, je potenciál na celé ploše elektrody stejný. Kapacitní a influenční koeficienty vyjadřujeme za předpokladu, že nulový potenciál jsme zvolili v nekonečnu.
Uvedené rovnice obvykle není snadné napsat přímo, ale můžeme je vyjádřit z rovnic pro potenciály, které sestavíme pomocí principu superpozice. Označíme si:
\(\varphi_{1}^{(1)}\) potenciál elektrického pole vytvořeného prvním nábojem na vnitřní (první) vrstvě a
\(\varphi_{1}^{(2)}\) potenciál elektrického pole vytvořeného druhým nábojem na vnitřní (druhé) vrstvě.
Analogicky pro vnější (druhou) vrstvu bude:
\(\varphi_{2}^{(1)}\) potenciál od prvního náboje na vnější (druhé) vrstvě,
\(\varphi_{2}^{(2)}\) potenciál od druhého náboje na vnější (druhé) vrstvě.
Pro celkový potenciál na vnitřní (první) vrstvě φ1 platí:
\[\varphi_{1}\,=\,\varphi_{1}^{(1)}\,+\,\varphi_{1}^{(2)}\]a na vnější (druhé) vrstvě:
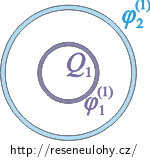
\[\varphi_{2}\,=\,\varphi_{2}^{(1)}\,+\,\varphi_{2}^{(2)}\,.\]Abychom vyjádřili potenciály, představíme si, že nejdříve nabijeme jenom vnitřní kulovou vrstvu nábojem Q1 a vyjádříme si potenciál \(\varphi_{1}^{(1)}\) na vnitřní vrstvě a potenciál \(\varphi_{2}^{(1)}\) na vnější vrstvě.
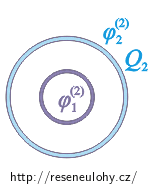
Nyní naopak nabijeme jenom vnější kulovou vrstvu nábojem Q2 a vyjádříme si potenciál \(\varphi_{1}^{(2)}\) na vnitřní vrstvě a potenciál \(\varphi_{2}^{(2)}\) na vnější vrstvě.
Tak sestavíme soustavu dvou rovnic, kterou si upravíme do tvaru (*), ze kterého vyjádříme kapacitní a influenční koeficienty.
b) Řešení: Kapacitní a influenční koeficienty
Pomocí principu superpozice si sestavíme dvě rovnice pro celkové potenciály na obou elektrodách:
\[\varphi_{1}\,=\,\varphi_{1}^{(1)}\,+\,\varphi_{1}^{(2)},\] \[\varphi_{2}\,=\,\varphi_{2}^{(1)}\,+\,\varphi_2^{(2)}.\tag{**}\]Pozn.: Značení je podrobněji vysvětleno v nápovědě.
Nejdříve si představíme, že nabijeme jenom vnitřní kulovou slupku nábojem Q1 a vyjádříme si potenciál \(\varphi_{1}^{(1)}\) na vnitřní slupce a potenciál \(\varphi_{2}^{(1)}\) na vnější slupce. Poté naopak budeme uvažovat, že nabijeme jenom vnější kulovou slupku nábojem Q2 a vyjádříme si potenciál \(\varphi_{1}^{(2)}\) na vnitřní slupce a potenciál \(\varphi_{2}^{(2)}\) na vnější slupce.
Potenciál vně tenké kulové slupky je dán vztahem \(\varphi (z)\,=\, \,\frac{Q}{4 \pi \varepsilon_0 }\,\frac{1}{z}\,=\, k\,\frac{Q}{z}\), kde z je vzdálenost od vrstvy. Uvnitř vrstvy je konstantní a stejný jako na povrchu vrstvy.
Jestliže nabijeme pouze vnitřní kulovou vrstvu nábojem Q1, bude na ní elektrický potenciál roven
\[\varphi_{1}^{(1)}\,=\, k\,\frac{Q_1}{R_1}\]a na vnější vrstvě bude potenciál roven
\[\varphi_{2}^{(1)}\,=\, k\,\frac{Q_1}{R_2}\,.\]Jestliže nabijeme pouze vnější kulovou vrstvu nábojem Q2, bude na ní elektrický potenciál roven
\[\varphi_{2}^{(2)}\,=\, \,k\,\frac{Q_2}{R_2}\,.\]Protože vnitřní vrstva je uvnitř vnější, bude na ní potenciál stejný:
\[\varphi_{1}^{(2)}\,=\, k\,\frac{Q_2}{R_2}\,.\]Vyjádřené vztahy dosadíme do rovnic (**) pro celkový potenciál obou vrstev a dostaneme:
\[\varphi_{1}\,=\,k\,\frac{Q_1}{R_1}\,+\,\,k\,\frac{Q_2}{R_2},\] \[\varphi_{2}\,=\,k\,\frac{Q_1}{R_2}\,+\,k\,\frac{Q_2}{R_2}.\]Nyní budeme soustavu rovnic upravovat tak, abychom vyjádřili náboje Q1 a Q2.
Vyjádření náboje Q1:
Nejdříve odečteme druhou rovnici od první. Tím získáme rovnici, ve které bude pouze náboj Q1:
\[\varphi_{1}\,-\,\varphi_{2}\,=\,k\,\frac{Q_1}{R_1}\,-\,k\,\frac{Q_1}{R_2}\]a ten vyjádříme:
\[\varphi_{1}\,-\,\varphi_{2}\,=\,kQ_1\,\left(\frac{1}{R_1}\,-\,\frac{1}{R_2}\right),\tag{***}\] \[\varphi_{1}\,-\,\varphi_{2}\,=\,kQ_1\,\frac{R_2\,-\,R_1}{R_1R_2} \hspace{40px}| \,\cdot \,\frac{R_1R_2}{k\,\left(R_2\,-\,R_1\right)}, \] \[Q_1\,=\,\frac{R_1R_2}{k\,\left(R_2\,-\,R_1\right)}\,\varphi_{1}\,-\,\frac{R_1R_2}{k\,\left(R_2\,-\,R_1\right)}\,\varphi_{2}. \tag{1}\]Vyjádření náboje Q2:
Obě rovnice vynásobíme uvedenými výrazy:
\[\varphi_{1}\,=\,k\,\frac{Q_1}{R_1}\,+\,k\,\frac{Q_2}{R_2}\hspace{40px}| \,\cdot \left( -R_1\right),\] \[\varphi_{2}\,=\,k\,\frac{Q_1}{R_2}\,+\,k\,\frac{Q_2}{R_2}\hspace{40px}| \,\cdot R_2. \]Rovnice odečteme:
\[ R_2 \varphi_{2} \,-\,R_1\varphi_{1}\,=\,k\, Q_2\,-\,k\,\frac{R_1}{R_2}\,Q_2\,\]a vyjádříme náboj Q2:
\[R_2 \varphi_{2} \,-\, R_1\varphi_{1}\,=\,kQ_2\,\left(1 \,-\,\frac{R_1}{R_2}\right), \] \[R_2 \varphi_{2} \,-\, R_1\varphi_{1}\,=\,kQ_2\,\frac{R_2\,-\, R_1}{R_2} \hspace{40px}| \,\cdot\frac{R_2}{k\,\left( R_2\,-\, R_1\right)},\] \[Q_2\,=\,\frac{R_2^2}{k\,\left( R_2\,-\, R_1 \right)}\,\varphi_2 \,-\, \frac{R_1R_2}{k\,\left(R_2 \,-\,R_1 \right)}\,\varphi_{01}.\tag{2}\]Získali jsme tedy dvě rovnice (1) a (2):
\[Q_1\,=\,\frac{R_1R_2}{k\,\left(R_2\,-\,R_1\right)}\,\varphi_{1}\,-\,\frac{R_1R_2}{k\,\left(R_2\,-\,R_1\right)}\,\varphi_{2}\,, \] \[Q_2\,=\,\,-\, \frac{R_1R_2}{k\,\left( R_2 \,-\, R_1\right)}\,\varphi_{1}\,+\,\frac{R_2^2}{k\,\left(R_2 \,-\, R_1 \right)}\,\varphi_{2}\,, \]ve kterých jsou již kapacitní a influenční koeficienty vyjádřeny.
Pro kapacitní koeficienty platí:
\[ C_{11}\,=\,\frac{R_1R_2}{k\,\left(R_2\,-\,R_1\right)},\] \[C_{22}\,=\,\frac{R_2^2}{k\,\left(R_2 \,-\, R_1\right)}\,.\]Influenční koeficienty C12 a C21 jsou stejné:
\[ C_{12}\,=\,C_{21}\,=\,-\,\frac{R_1R_2}{k\,\left( R_2\,-\, R_1 \right)}\,.\]Pozn.: Obecně platí, že kapacitní koeficienty jsou pro jakoukoli soustavu elektrod kladné a influenční koeficienty záporné. Navíc se influenční koeficienty s „prohozenými“ indexy vždy navzájem rovnají (tj. matice soustavy rovnic pro výpočet potenciálů je symetrická). Tyto obecné vlastnosti splňuje i soustava dvou soustředných kulových elektrod z naší úlohy.
Komentář: Kapacita kondenzátoru z předchozího oddílu
Kapacitu kondenzátoru můžeme vyjádřit také z rovnice (***) z předchozího oddílu. Vnitřní elektroda kondenzátoru je nabita nábojem Q:
\[\varphi_{1}\,-\,\varphi_{2}\,=\,kQ_1\,\left(\frac{1}{R_1}\,-\,\frac{1}{R_2}\right)\,=\,kQ\,\left(\frac{1}{R_1}\,-\,\frac{1}{R_2}\right).\]Rovnici upravíme, abychom na jedné straně měli podíl náboje Q a rozdílu potenciálů φ1 − φ2:
\[\varphi_{1}\,-\,\varphi_{2}\,=\,kQ\,\frac{R_2\,-\,R_1}{R_1R_2},\] \[(\varphi_{1}\,-\,\varphi_{2})\,\frac{R_1R_2}{k\left(R_2\,-\,R_1\right)}\,=\,Q\,,\] \[\,\frac{R_1R_2}{k\left(R_2\,-\,R_1\right)}\,=\,\frac{Q}{\varphi_{1}\,-\,\varphi_{2}}.\]Rozdíl potenciálu φ1 − φ2 na elektrodách kondenzátoru je roven napětí U na kondenzátoru:
\[\,\frac{R_1R_2}{k\left(R_2\,-\,R_1\right)}\,=\,\frac{Q}{U}.\]Podíl náboje Q a napětí U nám dává kapacitu kondenzátoru:
\[C\,=\,\frac{R_1R_2}{k\left(R_2\,-\,R_1\right)}.\]Vyšel nám stejný vztah jako při výpočtu s využitím intenzity.
Odpověď
Kapacita kulového kondenzátoru je dána vztahem
\[C\,=\,4 \pi \varepsilon_0 \,\frac{R_1 R_2}{R_2\,-\,R_1}\,.\]Pro kapacitní koeficienty C11 a C22 platí vztahy
\[ C_{11}\,=\,\frac{R_1R_2}{k\,\left(R_2\,-\,R_1\right)}\,,\] \[C_{22}\,=\,\frac{R_2^2}{k\,\left(R_2 \,-\, R_1\right)}\,.\]Influenční koeficienty C12 a C21 jsou stejné a jsou dány vztahem
\[ C_{12}\,=\,C_{21}\,=\,-\,\frac{R_1R_2}{k\,\left( R_2\,-\, R_1 \right)}\,.\]Ve všech vztazích platí, že \(k\,=\, \frac{1}{4 \pi \varepsilon_0}\).
Komentář: Kapacita pomocí koeficientů
V literatuře lze také nalézt vztah mezi kapacitou kondenzátoru a kapacitními a influenčními koeficienty:
\[C\,=\,\frac{C_{11}C_{22}\,-\,C_{12}^2}{C_{11}\,+\,2C_{12}\,+\,C_{22}}\,.\]Tento vztah zde nebudeme odvozovat, ale vyzkoušíme, jestli opravdu „funguje“ v našem případě.
Dosadíme do uvedeného vztahu koeficienty, které jsme si vyjádřili dříve:
\[C\,=\,\frac{ \frac{R_1R_2}{k\,\left(R_2\,-\,R_1\right)}\, \frac{R_2^2}{k\,\left( R_2\,-\, R_1 \right)}\,-\, \frac{R_1^2R_2^2}{k^2\,\left( R_2\,-\, R_1\right)^2}} {\frac{R_1R_2}{k\,\left(R_2\,-\,R_1\right)}\,-\, 2\frac{R_1R_2}{k\,\left(R_2 \,-\, R_1 \right)}\,+\, \frac{R_2^2}{k\,\left(R_2 \,-\, R_1\right)}}.\]Sečteme výrazy v čitateli a ve jmenovateli složeného zlomku:
\[C\,=\,\frac{ \frac{R_1R_2^3}{k^2\,\left( R_2\,-\, R_1 \right)^2}\,-\, \frac{R_1^2R_2^2}{k^2\,\left( R_2\,-\, R_1\right)^2}} {\frac{+R_1R_2\,-\,2R_1R_2\,+\,R_2^2}{k\,\left(R_2 \,-\, R_1\right)}},\] \[C\,=\,\frac{ \frac{R_1R_2^3\,-\,R_1^2R_2^2}{k^2\,\left( R_2\,-\, R_1\right)^2}} {\frac{\,-\,R_1R_2\,+\,R_2^2}{k\,\left(R_2 \,-\, R_1\right)}}.\] Zbavíme se složeného zlomku a zkrátíme stejné výrazy: \[C\,=\, \frac{R_1R_2^3\,-\,R_1^2R_2^2}{k^2\,\left( R_2\,-\, R_1\right)^2}\,\,\cdot\, \frac{k\,\left(R_2 \,-\, R_1\right)}{R_2^2\,-\,R_1R_2},\] \[C\,=\, \frac{R_1R_2^3\,-\,R_1^2R_2^2}{k\,\left( R_2\,-\, R_1\right)\left(R_2^2-\,R_1R_2\right)}.\]V čitateli i ve jmenovateli vytkneme stejné členy a opět zkrátíme:
\[C\,=\, \frac{R_1R_2^2 \left(R_2\,-\,R_1\right)}{k\,\left( R_2\,-\, R_1\right)\,R_2\,\left(R_2\,-\,R_1\right)},\] \[C\,=\, \frac{R_1R_2}{k\,\left( R_2\,-\, R_1\right)}.\]I pomocí uvedeného vztahu jsme získali pro kapacitu kondenzátoru stejný vztah.



