Sbírka řešených úloh

Potenciál bubliny a kapky

Úloha číslo: 35

Na jaký potenciál byla nabita mýdlová bublina o poloměru r_B = 3 cm, jestliže po prasknutí vznikne kapka o průměru d_K = 0,8 mm nabitá na potenciál φ_K = 60 kV.

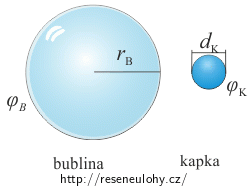
• Nápověda: Potenciál kapky a bubliny

  Potenciál v okolí a na povrchu kapky (koule) a bubliny (kulové vrstvy) je stejný jako potenciál v okolí a na povrchu bodového náboje.

• Nápověda: Náboj kapky a bubliny

  Rozmyslete si, zda se změní náboj bubliny, když praskne.

• Rozbor

  Potenciál v okolí a na povrchu bubliny (kulové vrstvy) a kapky (koule) je stejný jako potenciál v okolí bodového náboje, který by byl v jejich středu. Potenciál bodového náboje závisí přímo úměrně na velikosti náboje a nepřímo úměrně na vzdálenosti náboje a místa, ve kterém chceme potenciál zjistit.

  Při prasknutí bubliny se náboj nikam neztratí. Kapka proto bude mít stejný celkový náboj jako bublina. Potenciál se ale změní, jelikož kapka má menší poloměr.

  Porovnáním vztahů pro potenciály spočítáme potenciál kapky.

• Řešení

  Pro potenciál na povrchu bubliny (kulové vrstvy) a kapky (koule) platí stejný vztah jako pro bodový náboj

  \[\varphi\,=\,k \,\frac{Q}{r}\,,\]

  kde r je poloměr bubliny, resp. kapky.

  Když bublina praskne a změní se na kapku, zůstane náboj stejný.

  Potenciál kapky je tedy:

  \[\varphi_\mathrm{k}\,=\,k \,\frac{Q}{r_\mathrm{K}}\hspace{20px}\Rightarrow \hspace{20px} Q\,=\,\frac{\varphi_\mathrm{K} r_\mathrm{K}}{k}\tag{1}\]

  a potenciál bubliny:

  \[\varphi_\mathrm{b}\,=\,k \,\frac{Q}{r_\mathrm{B}} \hspace{20px}\Rightarrow\hspace{20px} Q\,=\,\frac{\varphi_\mathrm{B} r_\mathrm{B}}{k}.\tag{2}\]

  Vztahy pro náboje kapky (1) a bubliny (2) porovnáme:

  \[\frac{\varphi_\mathrm{B} r_\mathrm{B}}{k}\,=\,\frac{\varphi_\mathrm{K} r_\mathrm{K}}{k}.\]

  Všimněme si, že konstanta k se nám zkrátí a poměr potenciálů tedy závisí jen na poměru jejich poloměrů:

  \[\varphi_\mathrm{B} r_\mathrm{B}\,=\,\varphi_\mathrm{K} r_\mathrm{K}.\]

  Nyní si vyjádříme neznámý potenciál bubliny:

  \[\varphi_\mathrm{B}\,=\,\varphi_\mathrm{K} \, \frac{r_\mathrm{K}}{r_\mathrm{B}}.\]

• Zápis a číselný výpočet

  \[\varphi_\mathrm{K}\,=\,60\,\mathrm{kV}\,=\,6{\cdot} 10^4 \, \mathrm{V}\]

  Pozor! U kapky máme zadaný průměr, ale do výsledného vztahu potřebujeme poloměr:

  \[ \begin{eqnarray} d_\mathrm{K}\,&=&\,0{,}8 \,\mathrm{mm}\,\Rightarrow \,r_K\,=\,4{\cdot} 10^{-4}\, \mathrm{m}\\ r_\mathrm{B}\,&=&\,3 \,\mathrm{cm}\,=\,3{\cdot} 10^{-2}\, \mathrm{m}\\ \varphi_\mathrm{K}\,&=&\,?\,\left( \mathrm{V}\right)\end{eqnarray}\]

  ---

  \[\varphi_\mathrm{B}\,=\,\varphi_\mathrm{K} \, \frac{r_\mathrm{K}}{r_\mathrm{B}}\,=\,6{\cdot} 10^4 \,\cdot \frac{4{\cdot} 10^{-4}}{3{\cdot} 10^{-2}}\, \mathrm{V}\,=\,800 \, \mathrm{V}\]

  Vychází nám tedy, že potenciál bubliny je menší než potenciál kapky, což odpovídá tomu, že bublina je větší než kapka.

• Odpověď

  Bublina byla nabita na potenciál \(\varphi_\mathrm{B}\,=\,\varphi_\mathrm{K} \, \frac{r_\mathrm{K}}{r_\mathrm{B}}\,=\,800 \, \mathrm{V}\).