Příkon vařiče
Úloha číslo: 289
Ve vařiči jsou zabudovány dvě topné spirály s odpory 161,3 Ω a 60,5 Ω. S jakými příkony může vařič pracovat, pokud je připojen ke zdroji napětí 230 V, jestliže využijeme všechny možnosti zapojení topných spirál?
V této úloze považujeme odpory zapojených spirál za konstantní. V praxi však bude tato veličina záviset na tom, jak je spirála rozžhavená, tedy na napětí na spirále a proudu, který jí prochází.
Nápověda 1
Nakreslete si všechna možná zapojení jedné až dvou spirál (rezistorů) ke zdroji napětí. Celkem lze vytvořit čtyři různá zapojení.
Nápověda 2
Uvědomte si, co potřebujeme k výpočtu příkonu spotřebiče.
Rozbor
Pro dvě spirály existují čtyři různé způsoby zapojení:
- první spirálu zapojíme samostatně,
- druhou spirálu zapojíme samostatně,
- obě spirály jsou řazeny do série,
- spirály spojíme paralelně.
Příkon spotřebiče se rovná součinu napětí na spotřebiči a proudu, který spotřebičem protéká. Podle Ohmova zákona je proud protékající spotřebičem roven podílu napětí na spotřebiči a odporu spotřebiče.
Spotřebičem je v našem případě elektrický vařič. Celkové napětí na spotřebiči bude tedy stále stejné (hodnota napětí na vařiči 230 V ze zadání úlohy), proud procházející spotřebičem se bude měnit v závislosti na způsobu zapojení spirál.
Protože proud procházející vařičem se rovná podílu napětí na vařiči a odporu vařiče, můžeme příkon elektrického proudu vyjádřit jako podíl druhé mocniny napětí na vařiči a odporu vařiče.
Nyní si pro všechny způsoby zapojení vypočteme celkový odpor vařiče.
a) 
Pro první a druhou možnost, tj. jedna ze spirál je zapojena samostatně, je celkový odpor vařiče roven odporu spirály.
b) 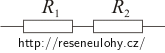
Jsou-li spirály řazeny do série, rovná se celkový odpor vařiče součtu odporů obou spirál.
c) 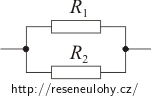
Pokud jsou spirály zapojeny paralelně, pak převrácená hodnota odporu vařiče se rovná součtu převrácených hodnot odporů obou spirál.
Řešení
Obecně pro příkon elektrického proudu platí:
\[P\,=\,UI,\]kde U je napětí na vařiči a I je proud procházející vařičem.
Proud I protékající vařičem se rovná podílu napětí na vařiči U a odporu vařiče R.
Tedy:
\[P\,=\,UI\,=\,U\frac{U}{R}\] \[P\,=\,\frac{U^2}{R}.\]Spirály můžeme zapojit čtyřmi různými způsoby: první spirálu zapojíme samostatně, druhou spirálu zapojíme samostatně, obě spirály jsou řazeny do série a poslední možností je spojit spirály paralelně.
a) Samostatně zapojená první spirála

Je-li vařič tvořen samostatnou první spirálou, pak pro příkon elektrického proudu tohoto zapojení platí:
\[P_1\,=\,\frac{U^2}{R_1},\]kde U je napětí na vařiči (je stejné jako napětí na spirále) a R1 je odpor spirály.
b) Samostatně zapojená druhá spirála

Příkon elektrického proudu vypočítáme stejně jako v předchozím případě. Tedy:
\[P_2\,=\,\frac{U^2}{R_2}.\]c) Sériově zapojené spirály

Spirály ve vařiči jsou zapojeny sériově, a proto je celkový odpor vařiče roven součtu odporů obou spirál. Tedy:
\[R\,=\,R_1\,+\,R_2.\]Pro příkon elektrického proudu tedy platí:
\[P_3\,=\,\frac{U^2}{R}\,=\,\frac{U^2}{R_1+R_2}.\]d) Paralelně zapojené spirály

Při paralelním zapojení spirál pro celkový odpor vařiče platí:
\[\frac{1}{R}\,=\,\frac{1}{R_1}\,+\,\frac{1}{R_2}\] \[\frac{1}{R}\,=\,\frac{R_1+R_2}{R_1R_2}.\]Pro příkon elektrického proudu platí:
\[P_4\,=\,\frac{U^2}{R}\,=\,U\frac{R_1+R_2}{R_1R_2}.\]Tedy:
\[P_4\,=\,\frac{U^2\left(R_1+R_2\right)}{R_1R_2}.\]Číselné dosazení
Ze zadání úlohy známe:
R1 = 161,3 Ω odpor první spirály R2 = 60,5 Ω odpor druhé spirály U = 230 V napětí na vařiči P1 = ? (W) příkon první spirály P2 = ? (W) příkon druhé spirály P3 = ? (W) příkon sériového zapojení spirál P1 = ? (W) příkon paralelního zapojení spirál
a) Samostatně zapojená první spirála
\[P_1\,=\,\frac{U^2}{R_1}\,=\,\frac{230^2}{161{,}3}\,\mathrm{W}\,=\,328\,\mathrm{W}\]b) Samostatně zapojená druhá spirála
\[P_2\,=\,\frac{U^2}{R_2}\,=\,\frac{230^2}{60{,}5}\,\mathrm{W}\,=\,874\,\mathrm{W}\]c) Sériově zapojené spirály
\[P_3\,=\,\frac{U^2}{R_1+R_2}\,=\,\frac{230^2}{161{,}3+60{,}5}\,\mathrm{W}\,=\,239\,\mathrm{W}\]d) Paralelně zapojené spirály
\[P_4\,=\,\frac{U^2\left(R_1+R_2\right)}{R_1R_2}\,=\,\frac{230^2\left(161{,}3+60{,}5\right)}{161{,}3{\cdot} 60{,}5}\,\mathrm{W}\,=\,1200\,\mathrm{W}\]Odpověď
Spirály můžeme zapojit čtyřmi různými způsoby, a tak získáme čtyři hodnoty příkonů, s jakými bude vařič pracovat při napětí 230 V.
Jestliže zapojíme samostatně první spirálu o odporu 161,3 Ω, pak vařič může pracovat s příkonem 328 W.
Při zapojení jen druhé spirály o odporu 60,5 Ω, pak vařič pracuje s příkonem 874 W.
Pokud spirály zapojíme do série, pak je příkon vařiče 239 W.
Jsou-li spirály zapojeny paralelně, má vařič příkon 1200 W.
Komentář
V této úloze jsme pracovali s efektivními hodnotami napětí a proudu. Efektivní hodnoty střídavého proudu a napětí odpovídají takovým hodnotám stejnosměrného proudu a napětí, při kterých je výkon stejnosměrného proudu v obvodu s odporem stejný jako výkon střídavého proudu. U topné spirály navíc můžeme zanedbat její indukčnost i kapacitu, a tedy i případné fázové posunutí mezi proudem a napětím. Z toho důvodu jsme úlohu mohli řešit, jako by byl vařič zapojen do obvodu se zdrojem stejnosměrného napětí.
Odkaz na podobnou úlohu
Podobnou úlohou, kterou si můžete vyzkoušet vyřešit, je úloha Zahradní párty s rychlovarnou konvicí




