Sbírka řešených úloh

Vodič ve tvaru pravého úhlu

Úloha číslo: 766

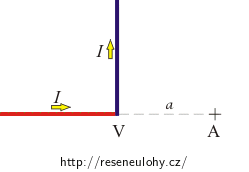
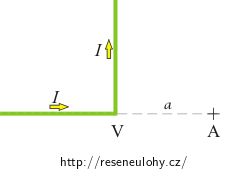
Velmi dlouhý vodič má tvar ramen pravého úhlu. Vypočtěte magnetickou indukci v bodě A vzdáleném a = 10 cm od vrcholu V (viz obrázek), když vodičem prochází proud I = 5 A .

• Nápověda

  Vodič si vhodně rozdělte na dvě části.

• Řešení nápovědy

  

  Celková magnetická indukce \(\vec B \) v bodě A bude dána vektorovým součtem indukcí vyvolaných oběma částmi vodiče.

• Řešení

  Při řešení úlohy budeme pro obě části vodiče postupovat podle Biotova-Savartova zákona

  \[\mathrm{d}\vec{B}= \frac{\mu_{0}I}{4\pi}\cdot \frac{\mathrm{d} \vec{l}\times \vec{r}}{r^{3}}\,.\]

  Kde \(\mathrm{d}\vec{l}\) je element vodiče a \(\vec{r}\) je polohový vektor směřující od elementu vodiče do bodu A.

• Řešení – červená část vodiče

  Indukci od červené části vodiče určíme velice jednoduše. Element vodiče \( \mathrm{d}\vec{l}\) a vektor vzdálenosti \(\vec{r}\) leží v jedné přímce. Vektorový součin dvou kolineárních vektorů je roven nule. Z tohoto důvodu bude nulový i přírůstek indukce vyvolaný daným kouskem vodiče, a tudíž i celková indukce vyvolaná červenou částí vodiče.

• Řešení – modrá část vodiče

  Indukci od modré části vodiče bychom mohli integrovat pomocí Biotova-Savartova zákona, ale jednodušší bude použít výsledek pro nekonečně dlouhý vodič, jehož výpočet je proveden v úloze Magnetické pole dlouhého přímého vodiče s proudem. Nekonečně dlouhý vodič by v bodě A vytvářel magnetickou indukci o velikosti  \[B=\frac {\mu_{0}I}{2\pi a},\] která by mířila ve směru tečny ke kružnici, která prochází bodem A a jejímž středem je nekonečný vodič. Podle Ampérova pravidla pravé ruky víme, že by směřovala do nákresny.

  Jelikož jsou úlohy symetrické, stačí si uvědomit, že část vodiče, která je v úloze přítomna, a část vodiče, která v úloze chybí, přispívají k celkové indukci stejně, proto pole jedné části vodiče musí být poloviční v porovnání s polem nekonečně dlouhého vodiče, tj. jeho velikost je \[B= \frac {1}{2}\cdot \frac {\mu_{0}I}{2\pi a}= \frac{\mu_{0}I}{4\pi a}\] a míří do nákresny.

• Celkové pole

  Při výpočtu používáme Biotův-Savartův zákon

  \[\mathrm{d}\vec{B}= \frac{\mu_{0}I}{4\pi}\cdot \frac{\mathrm{d} \vec{l}\times \vec{r}}{r^{3}}\,.\]

  

  Pro magnetickou indukci v bodě A můžeme psát

  \[\vec B= \vec{B_1}+\vec{B_2}\,.\]

  Příspěvek od červené části vodiče \(\vec {B_1}\) je nulový, protože element vodiče \( \mathrm{d}\vec{l}\) a vektor vzdálenosti \(\vec{r}\) leží v jedné přímce a vektorový součin dvou kolineárních vektorů je roven nule. Příspěvek od modré části vodiče \(\vec {B_2}\) určíme z výsledku magnetického pole v okolí nekonečně dlouhého přímého vodiče.

  Velikost celkové magnetické indukce je tedy

  \[ B = B_2 = \frac {1}{2}\cdot \frac {\mu_{0}I}{2\pi a}= \frac{\mu_{0}I}{4\pi a}\]

  a míří do nákresny.

• Zápis a číselné dosazení

  \( a=10\,\mathrm {cm} = 0{,}1\,\mathrm m\)		vzdálenost bodu A a V
  \(I= 5\,\mathrm A\)		proud procházející vodičem
  \(B\,=\,?\,\mathrm {(T)}\)		celková magnetická indukce
  Z tabulek:
  \(\mu_0 = 4 \pi\cdot 10^{-7}\,\mathrm{Hm^{-1}}\)		permeabilita vakua

  ---

  \[ B=\frac {\mu_0I}{4\pi a} =\frac{4\pi\cdot 10^{-7}\cdot5 }{4\pi\cdot0{,}1}\mathrm T=5{\cdot} 10^{-6}\,\mathrm{T}=5 \, \mu\mathrm {T}\]

• Odpověď

  Velikost magnetické indukce v bodě A je 5 μT.