Elektrické kyvadélko v poli nabité koule (malá výchylka)

Úloha číslo: 89

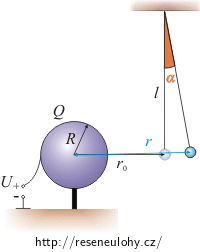
Na vlákně délky l = 12 cm je ve vzdálenosti r₀ = 5 cm od středu koule zavěšena kulička elektrického kyvadélka o hmotnosti m = 0,6 g. Kouli o poloměru R = 2 cm připojíme k jedné svorce zdroje o napětí U = 22 kV a druhou svorku uzemníme. Na kuličku kyvadélka přeneseme neznámý náboj q. Kulička kyvadélka se díky tomu vychýlí o malý úhel α = 5° od svislého směru. Náboje jsou souhlasné, a proto se odpuzují.

a) Jak velká elektrická síla působí na kuličku kyvadélka a jakou tahovou silou napíná kulička vlákno?

b) Jaký je náboj koule Q a náboj kuličky kyvadélka q?

Pozn.: Úhel α je malý, a proto uvažujeme, že kulička zůstala ve stejné výšce jako před nabitím.

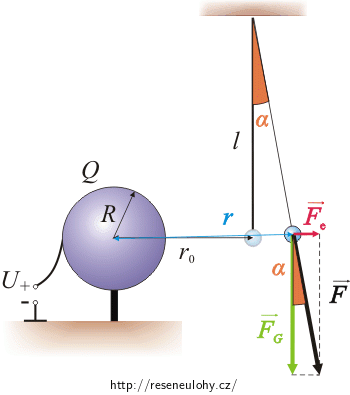
Obrázek působících sil
Nápověda: Výpočet tíhové síly a síly, kterou kulička napíná vlákno

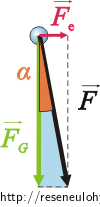
Velikost tíhové síly a síly, kterou kulička napíná vlákno, můžeme spočítat z modrého pravoúhlého trojúhelníka.
Nápověda: Výpočet náboje na kouli a na kuličce kyvadélka
Výpočet náboje na kouli:

Koule je vodivá, proto se na ni bude přesouvat náboj ze zdroje napětí až do doby, než bude potenciál na povrchu koule stejný jako potenciál zdroje.

Výpočet náboje na kuličce kyvadélka:

K výpočtu náboje na kuličce můžeme využít Coulombova zákona.
Rozbor
Výpočet sil:

Po zapnutí zdroje působí na kuličku odpudivá elektrická síla a tíhová síla. Výslednicí těchto dvou sil je síla, kterou kulička napíná provázek. Protože úhel vychýlení je malý, uvažujeme, že kulička zůstala po vychýlení ve stejné výšce, a síly tedy tvoří pravoúhlý trojúhelník. Velikost elektrické síly a síly, kterou kulička napíná provázek, spočítáme ze známé tíhové síly pomocí goniometrických funkcí.

Výpočet náboje na kouli:

Po připojení zdroje se bude náboj přesouvat na kouli až do té doby, než bude potenciál koule stejný jako potenciál zdroje (tj. stejný jako napětí na zdroji), protože druhá svorka je uzemněna. Koule je vodivá, proto všechen volný náboj bude na jejím povrchu. Potenciál na povrchu nabité koule je stejný jako potenciál v okolí bodového náboje.

Výpočet náboje na kuličce:

Velikost elektrické síly, která působí na kuličku, můžeme také spočítat z Colombova zákona. Z něho vyjádříme hledaný náboj.
Řešení: Výpočet tíhové síly a síly, kterou kulička napíná provázek

Na kuličku kyvadélka působí tíhová síla \(\vec{F}_\mathrm{G}\) a odpudivá elektrická síla \(\vec{F}_\mathrm{e}\). Výslednicí těchto dvou sil je síla \(\vec{F}\), kterou kulička napíná provázek.

Velikosti sil budeme počítat pomocí goniometrických funkcí z modrého pravoúhlého trojúhelníka.
Výpočet elektrické síly:
Velikost elektrické síly F_e vypočítáme pomocí známé tíhové síly F_G a tangenty úhlu α:
\[ \mathrm{tg}\, \alpha \,=\, \frac{F_\mathrm{e}}{F_\mathrm{G}}.\]
Vyjádříme sílu F_e:
\[F_\mathrm{e}\,=\, F_\mathrm{G} \, \mathrm{tg}\, \alpha.\]
Dosadíme za tíhovou sílu F_G = mg a získáme vztah pro výpočet elektrické síly:
\[F_\mathrm{e}\,=\, mg \, \mathrm{tg}\, \alpha.\] Výpočet síly provázku:
Sílu provázku F spočítáme podobně jako elektrickou sílu, ale pomocí kosinu úhlu α:
\[\cos \alpha \,=\, \frac{F_\mathrm{G}}{F}.\]
Vyjádříme sílu provázku F a dosadíme za tíhovou sílu F_G = mg:
\[F \,=\, \frac{F_\mathrm{G}}{\cos \alpha},\] \[F \,=\, \frac{mg}{\cos \alpha}.\]
Řešení: Výpočet náboje na kouli
Pro potenciál na povrchu nabité koule platí stejný vztah jako pro potenciál v okolí bodového náboje:
\[\varphi\,=\,\frac{1}{4\pi\epsilon_0}\,\frac{Q}{R}.\]
Protože je koule vodivá, je na jejím povrchu stejný potenciál, jako je napětí na zdroji, ke kterému jsme kouli připojili. Pokud by byl potenciál jiný, náboj by se přesouval ze zdroje na kouli (nebo obráceně) dokud by se potenciály nevyrovnaly:
\[U\,=\,\varphi\,=\,\frac{1}{4\pi\epsilon_0}\,\frac{Q}{R}.\]
Nyní stačí vyjádřit hledaný náboj Q:
\[Q\,=\,4\pi\epsilon_0 U R. \tag{*}\]
Řešení: Výpočet náboje na kuličce kyvadélka
Elektrickou sílu působící na kuličku můžeme vyjádřit z Coulombova zákona:
\[F_\mathrm{e}\,=\,\frac{1}{4\pi\epsilon_0} \,\frac{Qq}{r^2}.\]
Z tohoto vztahu si vyjádříme hledaný náboj q, který jsme přenesli na kuličku kyvadélka:
\[q\,=\,\frac{4\pi\epsilon_0 F_\mathrm{e} r^2 } {Q}.\]
Dosadíme za náboj koule ze vzorce (*) \(Q\,=\,4\pi\epsilon_0 U R\), který jsme si vyjádřili v předchozím oddíle Výpočet náboje na kouli:
\[q\,=\,\frac{4\pi\epsilon_0 F_\mathrm{e} r^2 } {4\pi\epsilon_0 U R}.\]
Zkrátíme:
\[q\,=\,\frac{F_\mathrm{e} r^2 } {U R}.\]
Velikost elektrické síly jsme vypočítali v oddíle Výpočet elektrické síly a síly, kterou kulička napíná provázek \(F_\mathrm{e}\,=\,mg \, \mathrm{tg}\, \alpha\), takže můžeme tento vztah dosadit:
\[q\,=\,\frac{mgr^2 \, \mathrm{tg} \alpha } {U R}.\tag{1}\]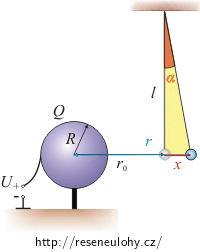

Nyní ještě potřebujeme vyjádřit vzdálenost r kuličky od koule (viz obrázek):
\[r\,=\,r_0+x.\]
Velikost úsečky x vypočítáme ze žlutého trojúhelníka pomocí funkce tangens:
\[r\,=\,r_0 +l \mathrm{tg}\, \alpha.\]
Vzdálenost r dosadíme do vzorce (1). Získali jsme konečný vztah pro výpočet náboje na kuličce:
\[q\,=\,\frac{mg \left(r_0 +l \mathrm{tg} \alpha \right)^2 \, \mathrm{tg}\, \alpha } {U R}.\]

Zápis a číselný výpočet

U = 22 kV = 2,2·10⁴ V	F_e = ? (N)
m = 0,6 g = 6·10⁻⁴ kg	F = ? (N)
l = 12 cm = 0,12 m	Q = ? (C)
R = 2 cm = 2·10⁻² m	q = ? (C)
r₀ = 5 cm = 5·10⁻² m	Z tabulek:
α = 5°	g = 9,8 ms⁻²
	ε₀ = 8,85·10⁻¹² C²N⁻¹m⁻²

Výpočet elektrické síly:

\[F_\mathrm{e}\,=\, mg \, \mathrm{tg} \alpha\,=\, 6 {\cdot} 10^{-4}\cdot 9{,}8 \cdot \mathrm{tg} 5^{\circ}\mathrm{N}\] \[F_\mathrm{e}\,=\,5{,}1{\cdot} 10^{-4} \, \mathrm{N}\]

Výpočet tahové síly:

\[F \,=\, \frac{mg}{\cos \alpha}=\, \frac{6 {\cdot} 10^{-4}\cdot 9{,}8}{\cos 5^{\circ}}\,\mathrm{N}\] \[F \,=\, 5{,}9{\cdot} 10^{-3} \,\mathrm{N}\]

Výpočet náboje na kouli:

\[Q\,=\,4\pi\epsilon_0 U R \,=\,4\pi\cdot 8{,}85{\cdot} 10^{-12} \cdot 2{,}2 {\cdot} 10^4 {\cdot} 2 \cdot 10^{-2}\,\mathrm{C}\] \[Q\,=\,4{,}8{\cdot} 10^{-8} \, \mathrm{C}\]

Výpočet náboje na kuličce kyvadélka:

\[q\,=\,\frac{mg \left(r_0 +l \mathrm{tg} \alpha \right)^2 \, \mathrm{tg} \alpha } {U R}\] \[q\,=\,\frac{6 {\cdot} 10^{-4}\cdot 9{,}8 \cdot \left(5 {\cdot} 10^{-2} +0{,}12 \cdot \mathrm{tg} 5^{\circ}\right)^2 \, \mathrm{tg} 5^{\circ} } {2{,}2 {\cdot} 10^4 {\cdot} 2 \cdot 10^{-2}}\mathrm{C}\,=\, 4{\cdot} 10^{-9}\,\mathrm{C}\]

Odpověď
Na kuličku kyvadélka působí elektrická síla \(F_\mathrm{e}\,=\, mg \, \mathrm{tg} \alpha\,=\,5{,}1{\cdot} 10^{-4} \, \mathrm{N}\) a kulička zároveň napíná vlákno silou \(F \,=\, \frac{mg}{\cos \alpha}=\, 5{,}9{\cdot} 10^{-3} \,\mathrm{N}\).

Po připojení zdroje je na kouli náboj \(Q\,=\,4\pi\epsilon_0 U R \,=\,\,4{,}8{\cdot} 10^{-8}\,\mathrm{C}\).

Zelektrovanou tyčí jsme na kuličku kyvadélka přenesli náboj \(q\,=\,\frac{mg \left(r_0 +l \mathrm{tg} \alpha \right)^2 \, \mathrm{tg} \alpha } {U R}\,=\, 4{\cdot} 10^{-9}\,\mathrm{C}\).
Odkaz na těžší úlohu
Pokud by se kulička vychýlila o větší úhel, nemohli bychom už úhel β zanedbat. Tento případ je vyřešen v úloze Elektrické kyvadélko v poli nabité koule (velká výchylka)