Termistor
Úloha číslo: 101
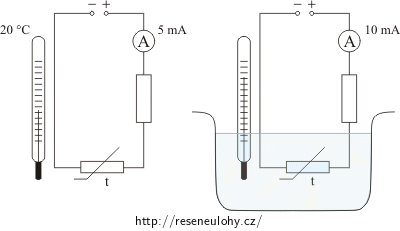
Ke zdroji o napětí 20 V je do série zapojen termistor a rezistor o odporu 1 kΩ. Při teplotě 20 °C jsme ampérmetrem naměřili v obvodu hodnotu proudu 5 mA. Po ponoření termistoru do teplé vody se proud v obvodu zvětšil na 10 mA.
Jaká je teplota vody, jestliže při vztažné teplotě 20 °C je střední hodnota teplotního součinitele odporu -0,04 K-1?
Nápověda
Vyhledejte si, co je termistor a jaké má vlastnosti.
Rozbor
Termistor je teplotně závislý rezistor. Jedná se o polovodičovou součástku, jejíž odpor se s rostoucí teplotou zmenšuje. Tato změna je daleko rychlejší než u kovů.
Mění-li se teplota termistoru pouze v malém rozmezí, můžeme říci, že závislost odporu na teplotě je prakticky lineární:
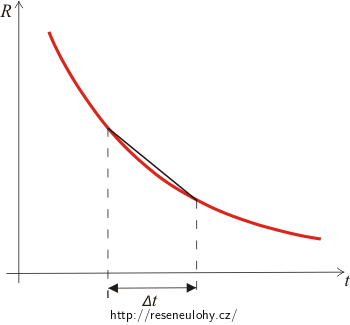
Změna odporu závisí na materiálu, z něhož je termistor vyroben (termistory se vyrábějí z oxidů kovů Mn, Fe, Co, Ni, ...). Tuto závislost charakterizuje tzv. teplotní součinitel elektrického odporu α. Jeho jednotkou je K-1. Hodnota α je závislá i na volbě vztažné teploty.
Pro některé látky jsou hodnoty α uvedeny v tabulkách.
Obecný výpočet
Závislost elektrického odporu termistoru na teplotě udává vztah
\[R_\mathrm{t}\,=\,R_\mathrm{t_0}\left(1+\alpha\Delta t\right)\,,\]kde Rt je odpor termistoru při teplotě t, Rt0 odpor termistoru při vztažné teplotě t0, α je teplotní součinitel elektrického odporu a Δt je rozdíl teplot Δt = t − t0.
Protože je ve vzorci teplotní rozdíl a protože pro termodynamickou a Celsiovu teplotu platí ΔT = Δt, nezáleží na tom, zda budeme teplotu dosazovat ve stupních Celsia nebo v kelvinech. V zadání úlohy máme teplotu vyjádřenou ve stupních Celsia, a proto i v dalších výpočtech budeme používat tyto jednotky.
Termistor je do obvodu připojen sériově, proto celkový odpor soustavy bude roven součtu odporu rezistoru a termistoru. Z Ohmova zákona víme, že pro náš obvod platí:
\[I\,=\,\frac{U}{R+R_\mathrm{t}}\hspace{30px}\Rightarrow\hspace{30px}R_\mathrm{t}\,=\,\frac{U}{I}-R\,,\]kde R je odpor rezistoru, Rt odpor termistoru, I je proud procházející obvodem a U je napětí na zdroji.
Pro počáteční teplotu 20 °C platí:
\[R_\mathrm{t_0}\,=\,\frac{U}{I_0}-R\,=\,\frac{U-RI_0}{I_0}\,.\]Po ponoření termistoru do teplé vody stoupne teplota. Pro odpor termistoru můžeme psát vztah:
\[R_\mathrm{t}\,=\,\frac{U}{I}-R\,=\,\frac{U-RI}{I}\,.\]Nyní si ze závislosti elektrického odporu termistoru na teplotě vyjádříme rozdíl teplot Δt:
\[ R_\mathrm{t}\,=\,R_\mathrm{t_0}\left(1+\alpha\Delta t\right) \] \[\alpha\Delta t\,=\,\frac{R_\mathrm{t}}{R_\mathrm{t_0}}-1\,.\]Dosadíme vyjádření obou odporů pomocí Ohmova zákona:
\[\alpha\Delta t\,=\,\frac{U-RI}{I}\cdot \frac{I_0}{U-RI_0}-1\] \[ \alpha\Delta{t}\,=\,\frac{I_0\left(U-RI\right)-I\left(U-RI_0\right)}{I\left(U-RI_0\right)}\,=\,\frac{I_0U-IU}{I\left(U-RI_0\right)} \] \[ \Delta t\,=\,t-t_0\,=\,\frac{U\left(I_0-I\right)}{\alpha I\left(U-RI_0\right)}\,. \]Pro teplotu termistoru získáme vztah:
\[ t\,=\,\frac{U\left(I_0-I\right)}{\alpha I\left(U-RI_0\right)}+t_0\,. \]Číselné dosazení
Ze zadání úlohy známe:
U = 20 V napětí zdroje R = 1 kΩ = 103 Ω odpor rezistoru α = -0,04 K-1 = -4·10-2 K-1 teplotní součinitel elektrického odporu t0 = 20 °C počáteční teplota I0 = 5 mA = 5·10-3 A hodnota proudu při počáteční teplotě t0 t = ? °C teplota vody I = 10 mA = 10·10-3 A = 10-2 A hodnota proudu při teplotě vody t
V předchozím oddíle jsme odvodili vztah pro teplotu termistoru:
\[ t\,=\,\frac{U\left(I_0-I\right)}{\alpha I\left(U-RI_0\right)}+t_0\,. \]Tato teplota je stejná jako teplota vody, do které je termistor ponořen.
Do vzorce dosadíme číselné hodnoty a vypočítáme teplotu vody, která zahřívá termistor:
\[ t\,=\,\frac{20\cdot\left(5-10\right)\cdot 10^{-3}}{-4{\cdot} 10^{-2}\cdot 10^{-2}\cdot\left(20-10^3{\cdot} 5\cdot 10^{-3}\right)}\,^{\circ}\mathrm{C}+20\,^{\circ}\mathrm{C} \] \[ t\,=\,\frac{-100{\cdot} 10^{-3}}{-60{\cdot} 10^{-4}}\,^{\circ}\mathrm{C}+20\,^{\circ}\mathrm{C}\,\dot{=}\,\left(16{,}7+20\right)\,^{\circ}\mathrm{C} \] \[ t\,\dot{=}\,37\,^{\circ}\mathrm{C}\,. \]Odpověď
Voda, do které jsme ponořili termistor, má teplotu 37 °C.
Odkaz na podobnou úlohu
Zkuste vyřešit také úlohu Odpor vodiče v závislosti na teplotě.




