Kapacita zapojení

Úloha číslo: 769

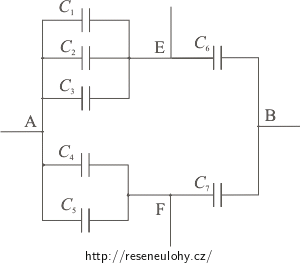
Najděte kapacitu mezi body A, B.

Přivedeme-li do bodu E náboj 90 µC, jaký bude rozdíl potenciálů mezi body E a F?

Kapacity kondenzátorů jsou:
C₁ = 6 µF, C₂ = 4 µF, C₃ = 2 µF, C₄ = 3 µF, C₅ = 1 µF, C₆ = 4 µF, C₇ = 2 µF.

Nápověda: Paralelní a sériové zapojení
Při paralelním zapojení kondenzátorů je celková kapacita rovna součtu jednotlivých kapacit:
\[C\,=\,C_1+C_2+C_3.\]
Při sériovém zapojení je převrácená hodnota celkové kapacity rovna součtu převrácených hodnot jednotlivých kapacit:
\[\frac{1}{C}\,=\,\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}.\]
Nápověda: Rozdíl potenciálů
Rozdíl potenciálů můžeme získat ze vztahu Q = CU.

Naším úkolem je tedy opět určit kapacitu, tentokrát mezi body E a F.
Rozbor
Kapacitu mezi body A a B určíme tak, že budeme postupně nahrazovat skupiny kondenzátorů zapojených sériově či paralelně jedním kondenzátorem. Kapacitu kondenzátoru určíme na základě známých vztahů pro spojování kondenzátorů.

Při paralelním zapojení kondenzátorů je celková kapacita rovna součtu jednotlivých kapacit. Při sériovém zapojení je převrácená hodnota celkové kapacity rovna součtu převrácených hodnot jednotlivých kapacit.

Postupnými úpravami budeme síť zjednodušovat, až nakonec zbude jediný kondenzátor, jehož kapacita bude rovna kapacitě mezi uvedenými body.

Při určování rozdílu potenciálů mezi body E a F budeme postupovat tak, že nejprve spočteme kapacitu mezi těmito body a poté využijeme známý vztah mezi napětím, kapacitou a nábojem.
Řešení: Kapacita
Kapacitu mezi body A a B určíme tak, že budeme postupně nahrazovat skupiny kondenzátorů zapojených sériově či paralelně jedním kondenzátorem, jehož kapacitu určíme na základě známých vztahů pro spojování kondenzátorů. Postupnými úpravami budeme síť zjednodušovat, až nakonec zbude jediný kondenzátor, jehož kapacita bude rovna kapacitě mezi uvedenými body.

Nejdříve nahradíme kondenzátory 1, 2 a 3 (v obrázku označeno červeně) novým kondenzátorem C_A.

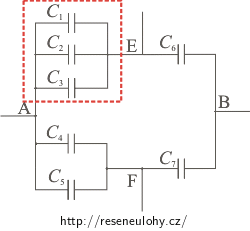
Bude platit:
\[C_\mathrm{A}\,=\,C_1\,+\,C_2\,+\,C_3\,.\]
Dále nahradíme kondenzátory 4 a 5 (označeny modře) kondenzátorem C_C a zároveň kondenzátory A a 6 (označeny zeleně) kondenzátorem C_B:

\[C_\mathrm{B}\,=\,\frac{C_\mathrm{A} C_6}{C_\mathrm{A}\,+\,C_6}\,=\,\frac{\left(C_1\,+\,C_2\,+\,C_3 \right) C_6}{C_1\,+\,C_2\,+\,C_3\,+\, C_6}\] \[C_\mathrm{C}\,=\,C_4\,+\,C_5.\]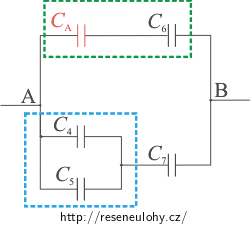
Nyní nahradíme kondenzátory C a 7 (označeno oranžovou) kondenzátorem C_D:

\[C_\mathrm{D}\,=\,\frac{C_\mathrm{C} C_7}{C_\mathrm{C}\,+\,C_7}\,=\,\frac{\left(C_4\,+\,C_5 \right) C_7}{C_4\,+\,C_5\,+\,C_7}.\]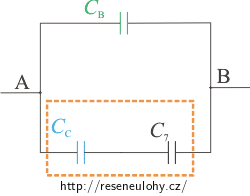
Poslední úpravou už získáme obvod s jedním kondenzátorem:

\[C_\mathrm{V}\,=\,C_\mathrm{B}+C_\mathrm{D}.\]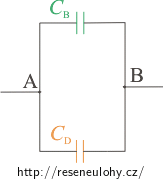

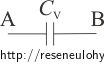
Celková kapacita mezi body A a B je tedy:
\[C_\mathrm{V}\,=\,\frac{\left(C_1\,+\,C_2\,+\,C_3 \right) C_6}{C_1\,+\,C_2\,+\,C_3\,+\, C_6}\,+\,\frac{\left(C_4\,+\,C_5 \right) C_7}{C_4\,+\,C_5\,+\,C_7}\,.\]
Řešení: Rozdíl potenciálů
Při určování rozdílu potenciálů mezi body E a F budeme postupovat tak, že nejprve spočteme kapacitu mezi těmito body a poté využijeme známý vztah Q = CU. Při počítání kapacity budeme používat postup popsaný v první části této úlohy.

Nejdříve nahradíme kondenzátory 1, 2 a 3 (označeno červeně) kondenzátorem C_R.

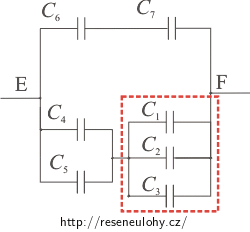
Bude platit:
\[C_\mathrm{R}\,=\,C_1\,+\,C_2\,+\,C_3\,.\]
Dále nahradíme kondenzátory 4 a 5 (označeno zeleně) kondenzátorem C_S a zároveň kondenzátory 6 a 7 (označeno modře) kondenzátorem C_T:

\[C_\mathrm{S}\,=\,C_4\,+\,C_5\] \[C_\mathrm{T}\,=\,\frac{C_6 C_7}{C_6\,+\,C_7}.\]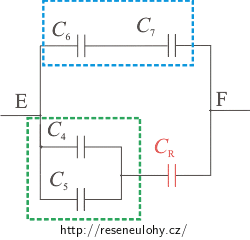
Nyní nahradíme kondenzátory R a S (označeno oranžovou) kondenzátorem C_U:

\[C_\mathrm{U}\,=\,\frac{C_\mathrm{R} C_\mathrm{S}}{C_\mathrm{R}+ C_\mathrm{S}}\,=\,\frac{\left(C_1\,+\,C_2\,+\,C_3 \right) \left(C_4\,+\,C_5\right)}{C_1\,+\,C_2\,+\,C_3\,+\, C_4\,+\,C_5}.\]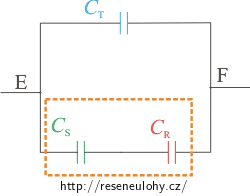
Poslední úpravou už získáme obvod s jedním kondenzátorem:

\[C_\mathrm{V2}\,=\,C_\mathrm{T}+C_\mathrm{U}\]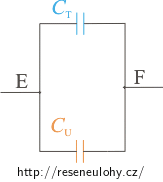

\[C_\mathrm{V2}\,=\,\frac{\left(C_1\,+\,C_2\,+\,C_3 \right) \left(C_4\,+\,C_5\right)}{C_1\,+\,C_2\,+\,C_3\,+\, C_4\,+\,C_5}\,+\,\frac{C_6 C_7}{C_6\,+\,C_7}.\]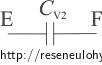
Rozdíl potenciálů mezi body E a F určíme ze vztahu:
\[U\,=\,\frac{Q}{C}\,.\] \[U\,=\,\frac{Q}{\frac{\left(C_1\,+\,C_2\,+\,C_3 \right) \left(C_4\,+\,C_5\right)}{C_1\,+\,C_2\,+\,C_3\,+\, C_4\,+\,C_5}\,+\,\frac{C_6 C_7}{C_6\,+\,C_7}}.\]
Zápis a číselný výpočet
C₁ = 6 µF

C₂ = 4 µF

C₃ = 2 µF

C₄ = 3 µF

C₅ = 1 µF

C₆ = 4 µF

C₇ = 2 µF

Q = 90 µC

C_V1 = ? µF

U = ? V

\[C_\mathrm{V1}\,=\,\frac{\left(C_1\,+\,C_2\,+\,C_3 \right) C_6}{C_1\,+\,C_2\,+\,C_3\,+\, C_6}\,+\,\frac{\left(C_4\,+\,C_5 \right) C_7}{C_4\,+\,C_5\,+\,C_7}\] \[C_\mathrm{V1}\,=\,\left(\frac{\left(6\,+\,4\,+\,2 \right) 4}{6\,+\,4\,+\,2\,+\, 4}\,+\,\frac{\left(3\,+\,1 \right) 2}{3\,+\,1\,+\,2}\right)\,\mathrm{\mu F}\,\dot=\,4{,}3\,\mathrm{\mu F}\] \[C_\mathrm{V2}\,=\,\frac{\left(C_1\,+\,C_2\,+\,C_3 \right) \left(C_4\,+\,C_5\right)}{C_1\,+\,C_2\,+\,C_3\,+\, C_4\,+\,C_5}\,+\,\frac{C_6 C_7}{C_6\,+\,C_7}\] \[C_\mathrm{V2}\,=\,\left(\frac{\left(6\,+\,4\,+\,2 \right) \left(3\,+\,1\right)}{6\,+\,4\,+\,2\,+\, 3\,+\,1}\,+\,\frac{4{\cdot} 2}{4\,+\,2}\right)\mathrm{\mu F}\,\dot=\,4{,}3\,\mathrm{\mu F}\] \[U\,=\,\frac{Q}{\frac{\left(C_1\,+\,C_2\,+\,C_3 \right) \left(C_4\,+\,C_5\right)}{C_1\,+\,C_2\,+\,C_3\,+\, C_4\,+\,C_5}\,+\,\frac{C_6 C_7}{C_6\,+\,C_7}}\] \[U\,=\,\frac{90}{\frac{\left(6\,+\,4\,+\,2 \right) \left(3\,+\,1\right)}{6\,+\,4\,+\,2\,+\, 3\,+\,1}\,+\,\frac{4 {\cdot} 2}{4\,+\,2}}\,\dot=\,21\,\mathrm{V}\]
Odpověď
Kapacita mezi body A a B je
\[C_\mathrm{V1}\,=\,\frac{\left(C_1\,+\,C_2\,+\,C_3 \right) C_6}{C_1\,+\,C_2\,+\,C_3\,+\, C_6}\,+\,\frac{\left(C_4\,+\,C_5 \right) C_7}{C_4\,+\,C_5\,+\,C_7}\,\dot=\,4{,}3\,\mathrm{\mu F}\,.\]
Rozdíl potenciálů mezi body E a F je
\[U\,=\,\frac{Q}{\frac{\left(C_1\,+\,C_2\,+\,C_3 \right) \left(C_4\,+\,C_5\right)}{C_1\,+\,C_2\,+\,C_3\,+\, C_4\,+\,C_5}\,+\,\frac{C_6 C_7}{C_6\,+\,C_7}}\,\dot=\,21\,\mathrm{V}\,.\]