Sbírka řešených úloh

Kulička ve vzduchu spojená s kuličkou v oleji

Úloha číslo: 779

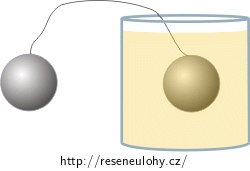
Dvě kovové kuličky mají stejný poloměr a stejný náboj 4·10⁻⁹ C. Jedna kulička je ponořena do nádoby s olejem o relativní permitivitě 3 a druhá je ve vzduchu.

Jak velké budou náboje na kuličkách, spojíme-li je drátem?

• Nápověda

  Co se může dít poté, co kuličky propojíme drátem?

  Má to nějakou souvislost s potenciálem obou kuliček?

  Jak ovlivňuje elektrické pole olej, do kterého je druhá kulička ponořena?

• Řešení nápovědy

  Spojíme-li nabité vodivé kuličky drátem, bude se přesouvat náboj z jedné kuličky na druhou do té doby, než budou mít obě stejný potenciál.

  Potenciál nabité kuličky závisí přímo úměrně na náboji koule a nepřímo úměrně na jejím poloměru a permitivitě prostředí, ve kterém je.

• Rozbor

  Potenciál nabité kuličky závisí přímo úměrně na velikosti náboje a nepřímo úměrně na poloměru kuličky a permitivitě prostředí, ve kterém kulička je. To znamená, že potenciál kuličky ponořené v oleji je menší než potenciál kuličky na vzduchu. Po spojení obou kuliček drátem tedy přejde část náboje z kuličky na vzduchu na kuličku v oleji. Celkový náboj na obou kuličkách však musí být stejný jako před spojením vodičem.

  Náboj bude přecházet až do chvíle, kdy se na obou kuličkách vyrovnají potenciály. Poté se soustava ustálí a k dalším přesunům náboje již nebude docházet. V tomto ustáleném stavu tedy bude potenciál obou kuliček stejný.

• Řešení

  Po spojení obou kuliček drátem může přejít část náboje z jedné kuličky na druhou. Celkový náboj na obou kuličkách však musí být stejný jako před spojením vodičem.

  Označíme-li si náboj na kuličce ve vzduchu Q_v a v oleji Q_o bude platit vztah:

  $$2Q\,=\,Q_\mathrm{v}\,+\,Q_\mathrm{o}\,.\tag{1}$$

  Náboj mezi kuličkami bude přecházet až do chvíle, kdy se na obou kuličkách vyrovnají potenciály. Poté se soustava ustálí a k dalším přesunům náboje již nebude docházet. V tomto ustáleném stavu tedy bude potenciál obou kuliček stejný:

  $$\varphi_\mathrm{v}\,=\,\varphi_\mathrm{o}.\tag{*}$$

  Pro potenciál kuličky platí vztah

  $$\varphi\,=\, \frac{1}{4 \pi \varepsilon}\,\frac{Q}{r}\,,$$

  kde r je poloměr kuličky a ε je permitivita prostředí okolo kuličky.

  Tento vztah dosadíme do vzorce (*). První kulička je ve vzduchu, jehož permitivita je ε₀, druhá kulička je v oleji, jehož permitivita je ε_r-krát větší:

  $$\frac{1}{4 \pi \varepsilon_0}\,\frac{Q_\mathrm{v}}{r}\,=\, \frac{1}{4 \pi \varepsilon_0 \varepsilon_\mathrm{r}}\,\frac{Q_\mathrm{o}}{r}.$$

  Zkrátíme stejné veličiny a vyjádříme náboj Q_o:

  $$Q_\mathrm{v}\,=\, \frac{Q_\mathrm{o}}{ \varepsilon_\mathrm{r}}$$ $$Q_\mathrm{o}\,=\, Q_\mathrm{v} \varepsilon_\mathrm{r}.\tag{2}$$

  Zkombinováním vztahů (1) a (2) vyjádříme nejdříve náboj kuličky ve vzduchu a poté kuličky v oleji.

  Do vztahu (1) dosadíme vztah (2):

  $$2Q\,=\,Q_\mathrm{v}\,+\,Q_\mathrm{v} \varepsilon_\mathrm{r}.$$

  Vytkneme náboj Q_v a vyjádříme ho:

  $$2Q\,=\,Q_\mathrm{v} \left(1\,+\, \varepsilon_\mathrm{r} \right)$$ $$Q_\mathrm{v}\,=\,\frac{2Q}{1\,+\, \varepsilon_\mathrm{r}}.$$

  Náboj kuličky v oleji získáme dosazením předchozího vztahu do vzorce (2):

  $$Q_\mathrm{o}\,=\, Q_\mathrm{v} \varepsilon_\mathrm{r}$$ $$Q_\mathrm{o}\,=\, \frac{2Q \varepsilon_\mathrm{r}}{1\,+\, \varepsilon_\mathrm{r}}.$$

  Po spojení kuliček bude na kuličce ve vzduchu náboj $Q_\mathrm{v}\,=\,\frac{2Q}{1\,+\, \varepsilon_\mathrm{r}}$ a na kuličce v oleji náboj $Q_\mathrm{o}\,=\, \frac{2Q \varepsilon_\mathrm{r}}{1\,+\, \varepsilon_\mathrm{r}}$.

• Zápis a číselný výpočet

  Q = 4· 10⁻⁹ C

  ε_r = 3

  Q_v = ? (C)

  Q_o = ? (C)

  Z tabulek

  ε₀ = 8,85·10⁻¹² C²N⁻¹m⁻²

  ---

  $$Q_\mathrm{v}\,=\,\frac{2Q}{1\,+\, \varepsilon_\mathrm{r}}\,=\,\frac{2{\cdot} 4\cdot 10^{-9}}{1\,+\, 3}\,\mathrm{C}\,=\,2{\cdot} 10^{-9}\,\mathrm{C}\,=\,2\,\mathrm{nC}$$ $$Q_\mathrm{o}\,=\, \frac{2Q \varepsilon_\mathrm{r}}{1\,+\, \varepsilon_\mathrm{r}}\,=\,\frac{2{\cdot} 4\cdot 10^{-9}\cdot 3}{1\,+\, 3}\,\mathrm{C}\,=\,6{\cdot} 10^{-9}\,\mathrm{C}\,=\,6\,\mathrm{nC}$$

  Vidíme, že náboj přecházel z kuličky na vzduchu na kuličku v oleji. To přesně odpovídá tomu, že vyšší permitivita oleje zmenšuje potenciál kuličky v něm ponořené.

• Odpověď

  Po spojení kuliček bude na kuličce ve vzduchu náboj

  $$Q_\mathrm{v}\,=\,\frac{2Q}{1\,+\, \varepsilon_\mathrm{r}}\,=\,2\,\mathrm{nC}$$

  a na kuličce v oleji náboj

  $$Q_\mathrm{o}\,=\, \frac{2Q \varepsilon_\mathrm{r}}{1\,+\, \varepsilon_\mathrm{r}}\,=\,6\,\mathrm{nC}\,.$$

• Odkaz na podobnou úlohu

  Jak by se situace změnila, pokud by byly kuličky ve stejném prostředí, ale měly různou velikost, zjistíte v úloze Nabité koule spojené drátem.