Nehomogenní proudová hustota
Úloha číslo: 2307
Uvažujme nekonečně dlouhý válcový vodič s poloměrem R, kterým protéká proud I s nehomogenní proudovou hustotou \(j= \alpha r,\) kde \(\alpha\) je konstanta. Najděte průběh magnetického pole.
Nápověda
Úlohu budeme řešit pomocí Ampérova zákona. Připomeňme si jeho znění: „Celkový proud procházející plochou, kterou ohraničuje uzavřená křivka, vynásobený permeabilitou vakua se rovná integrálu magnetické indukce podél této křivky.“ Matematicky zapíšeme jako
\[\mu_0I_\mathrm{c}=\oint_\Gamma \vec{B}\cdot \vec{\mathrm{d}l}.\]Jakou křivku zvolíme jako Ampérovu křivku v naší úloze?
Řešení − celkový proud
Pro celkový proud procházející vodičem s homogenní proudovou hustotu \(\vec{j}\) platí
\[I_\mathrm{c}=\vec{j}\cdot\vec{S}.\]V našem případě ale nemáme homogenní proudovou hustotu, a tudíž budeme muset celkový proud naintegrovat:
\[I_\mathrm{c}=\int_\mathrm{S} {j}{\mathrm{d}S},\]kde \(\mathrm{d}S\) je infinitezimální příspěvek obsahu, který můžeme pomocí polárních souřadnic rozepsat jako
\[ \mathrm{d}S=\rho \mathrm{d}\rho \mathrm{d}\varphi.\]Viz Obsah infinitezimální plochy kruhu.
\[I_\mathrm{c}=\int_0^{2\pi}\int_0^\mathrm{R} \alpha \rho \thinspace\mathrm{d}\rho \mathrm{d}\varphi=\int_0^\mathrm{R}\alpha \rho 2 \pi \rho \thinspace\mathrm{d}\rho=2 \pi\alpha\int_0^\mathrm{R} \rho^2 \thinspace \mathrm{d}\rho, \] \[I_\mathrm{c}=2 \pi\alpha\left[\frac{\rho^3}{3}\right]_0^\mathrm{R}=\frac{2\pi\alpha R^3}{3}.\]Pozn.: Spočítali jsme proud procházející celým průřezem vodiče. Pokud bychom potřebovali vyjádřit proud procházející průřezem o poloměru \({r}<R\), výpočet bude stejný, jen se změní mez u souřadnice \(\rho\)
a dostaneme \[\widehat{I_\mathrm{c}}=2 \pi\alpha\left[\frac{\rho^3}{3}\right]_0^\mathrm{r}=\frac{2\pi\alpha r^3}{3}.\]Řešení
Řešení úlohy rozdělíme na dvě části. Nejprve určíme průběh magnetického pole vně vodiče a poté uvnitř vodiče.
V řešení předpokládáme, že proud vodičem teče směrem z nákresny k nám. Dále předpokládáme, že vektor proudové hustoty je kolmý na průřez vodiče.
a) Magnetické pole vně vodiče
Pro řešení využijeme Ampérova zákonu:
\[I_\mathrm{c}\mu_0=\oint_\Gamma \vec{B}\cdot \vec{\mathrm{d}l}.\]Jako Ampérovu smyčku \(\Gamma\) budeme volit kružnici o poloměru \(r>R\) se středem uprostřed řezu válce, viz obrázek, kde smyčka je naznačena tečkovaně.
\[I_\mathrm{c}\mu_0=\oint_\Gamma \vec{B}\cdot \vec{\mathrm{d}l}\]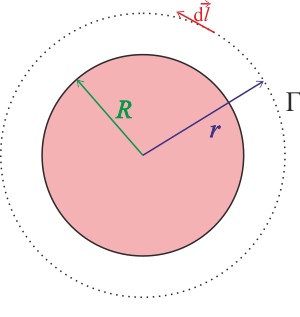
Jako Ampérovu smyčku jsme zvolili kružnici \(\Gamma\). Ze symetrie rozložení proudu víme, že v každém bodě kružnice \(\Gamma\) je směr magnetické indukce \(\vec{B}\) tečný k této kružnici (viz Ampérovo pravidlo pravé ruky). Vektor posunutí \(\mathrm{d}\vec{l}\) je také tečný ke kružnici, proto platí
\[|\vec{B}\cdot \mathrm{d}\vec{l}|=B\mathrm{d}l.\]A jelikož nás zajímá velikost magnetické indukce, můžeme psát
\[I_\mathrm{c}\mu_0=\oint_\Gamma {B}{\mathrm{d}l}.\]Díky tomu, že má \(B\) po celém obvodu křivky stejnou hodnotu, můžeme vytknout před integrál:
\[I_\mathrm{c}\mu_0={B}\oint_\Gamma 1 {\mathrm{d}l}.\]Integrál z jedničky přes uzavřenou křivku je délka této křivky. V našem případě se jedná o obvod kružnice o poloměru \({r}\), kterou jsme zvolili jako Ampérovu smyčku. Dostáváme
\[I_\mathrm{c}\mu_0={B}\,2\pi{r},\] \[ B=\frac{\mu_0} {2\pi}\frac{I_\mathrm{c}}{r}.\]Po porovnání výsledku s magnetickým polem v okolí tenkého přímého vodiče (Magnetické pole přímého vodiče) zjistíme, že vodič s nehomogenní, ale osově symetricky rozloženou proudovou hustotou se z hlediska magnetického pole vně vodiče chová stejně jako tenký přímý vodič, kterým prochází proud \(I_\mathrm{c}.\)
Nyní za celkový proud dosaďme hodnotu vyjádřenou v předchozím oddíle:
\[I_\mathrm{c}=\frac{2\pi\alpha R^3}{3},\] \[B=\frac{\mu_0\alpha R^3}{3r}.\]b) Magnetické pole uvnitř vodiče
Tuto část budeme opět řešit pomocí Ampérova zákona. Jako Ampérovu smyčku budeme znovu volit kružnici se středem uprostřed řezu válcového vodiče. Jelikož budeme vyšetřovat magnetické pole uvnitř vodiče, bude platit \(R>r\).
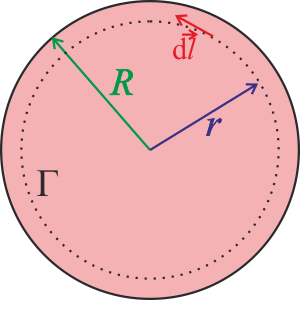
Zaměříme se pouze na velikost magnetické indukce, a proto Ampérův zákon přepíšeme do skalárů:
\[\widehat{I_\mathrm{c}}\mu_0=\oint_\Gamma {B}{\mathrm{d}l}.\]Pozn.: \(\widehat{I_\mathrm{c}}\) je proud procházející průřezem vodiče o poloměru r (v našem případě plochou Ampérovy křivky o poloměru r), viz předchozí oddíl.
Stejně jako v části a) má \(\vec{B}\) po celém obvodu křivky stejnou velikost, můžeme ji vytknout před integrál a integrál z jedničky nám dá délku křivky:
\[\widehat{I_\mathrm{c}}\mu_0={B}\oint_\Gamma 1 {\mathrm{d}l}={B}2\pi{r}\]a po vyjádření dostaneme
\[B=\frac{\mu_0 }{2\pi }\frac{\widehat{I_\mathrm{c}}}{r}.\]Za celkový proud dosaďme hodnotu vyjádřenou v předchozím oddíle:
\[{\widehat{I_\mathrm{c}}}=2 \pi\alpha\left[\frac{\rho^3}{3}\right]_0^\mathrm{r}=\frac{2\pi\alpha r^3}{3},\] \[B=\frac{\mu_0 \alpha r^2 }{3 }.\]Porovnáme-li magnetické pole uvnitř našeho vodiče s nehomogenní proudovou hustotou a magnetické pole uvnitř tlustého přímého vodiče s homogenně rozloženou proudovou hustotou (Magnetické pole přímého vodiče), zjistíme, že velikost magnetického pole závisí na vzdálenosti od osy vodiče odlišně.
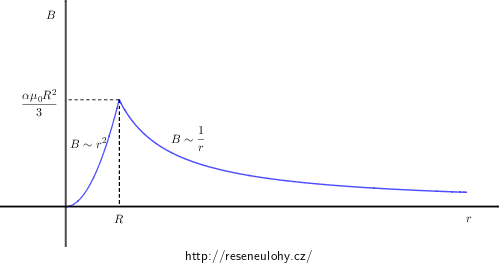
Všimněte si spojitosti magnetické indukce B na povrchu vodiče. Spojitost odpovídá teorii, protože magnetická indukce je nespojitá pouze v místech, kde teče plošný proud. Naším vodičem protéká pouze objemově rozložený proud.
Pozn.: Proud, který teče mimo Ampérovu smyčku, nepřispívá k magnetické indukci, respektive se jeho příspěvky navzájem vyruší.
Pozn.: Pro provedené výpočty (v obou částech) je důležité, že proudová hustota závisí pouze na vzdálenosti od středu vodiče (má válcovou symetrii). Bez tohoto předpokladu bychom nemohli použít Ampérův zákon takto jednoduše.
Odpověď
Vzhledem k symetrii situace je směr magnetického pole tečný ke kružnici se středem uprostřed řezu vodiče.
Magnetické pole ve vzdálenosti \(r>R\) (vně vodiče) má velikost
\[B=\frac{\alpha \mu_0 R^3}{3r}=\frac{\mu_0}{2\pi}\frac{I_c\mathrm{c}}{r}\]a chová se stejně jako magnetické pole tenkého přímého vodiče, kterým prochází proud \(I_\mathrm{c}.\)
Ve vzdálenosti \(r < R\) (uvnitř vodiče) je velikost magnetického pole
\[B=\frac{\alpha \mu_0 r^2}{3}=\frac{\mu_0}{2\pi}\frac{\widehat{I_\mathrm{c}}}{r}.\]Následující obrázek zobrazuje graf průběhu velikosti magnetického pole v závislosti na vzdálenosti r od středu vodiče.


