Cyklotron
Úloha číslo: 310
Jádra těžkého vodíku, deuterony, jsou urychlovány v kruhovém urychlovači, cyklotronu. Určete frekvenci, jakou musí mít zdroj napětí cyklotronu, je-li velikost magnetického pole v urychlovači 1,5 T a deuterony mají hmotnost 3,3·10-27 kg.
Jak velký musí být poloměr cyklotronu, jestliže částice opouští urychlovač s kinetickou energií 16 MeV? Kolikrát proběhne deuteron mezi duanty cyklotronu, je-li mezi nimi potenciální rozdíl 50 kV?
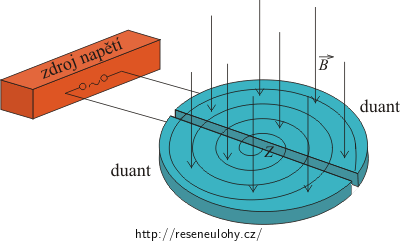
Popis funkce cyklotronu
Cyklotron je zařízení, které urychluje nabité částice, tj. umožňuje jim získat velkou kinetickou energii. Tyto vysoce energetické částice se dále využívají např. v jaderném výzkumu nebo v nemocnicích k získání radioaktivních preparátů k léčebným a diagnostickým účelům.
Cyklotron je tvořen dvěma půlválcovými vodiči ve tvaru písmene D, otevřenými na rovné straně. Vodiče jsou vyrobeny z neferomagnetického materiálu (např. měděných plechů) a nazývají se duanty. Jsou umístěny v homogenním magnetickém poli o velké magnetické indukci, která je kolmá na vodiče. Mezi vodiči je mezera, na kterou je přivedeno střídavé napětí. Jestliže nabitá částice vstoupí v blízkosti středu cyklotronu do elektrického pole mezi duanty, je v prostoru mezi nimi urychlena a získá rychlost, se kterou vstupuje kolmo do magnetického pole uvnitř jednoho z duantů.
Magnetické pole zakřiví její dráhu, takže v prostoru duantu opíše půlkružnici. V okamžiku, kdy částice vystoupí z tohoto duantu, změní elektrické pole mezi duanty svou orientaci a částice je opět urychlena směrem do druhého duantu. Její větší rychlost znamená větší poloměr kružnicové trajektorie. Tento proces se opakuje a tím vzniká trajektorie, která je tvořena půlkružnicemi a úsečkami (viz obrázek u zadání úlohy). V okamžiku, kdy poloměr trajektorie dosáhne poloměru cyklotronu, částice s velkou kinetickou energií vystupuje z cyklotronu.
Celý trik cyklotronu spočívá v tom, že se zároveň zvyšuje rychlost částice i délka její trajektorie (délka půlkružnice) tak, že doba letu po kružnici zůstává konstantní (což je v řešení úlohy podrobně odvozeno). Díky tomu stačí mezi duanty připojit pole s konstantní frekvencí (bude vždy urychlovat správným směrem) a není třeba měnit frekvenci elektrického pole (časovou vzdálenost napěťových pulzů) podle toho, jak jsou částice urychlené.
Rozbor
Deuteron, který vylétl ze zdroje Z ve středu cyklotronu, se zpočátku pohybuje směrem k záporně nabitému duantu (protože deuteron je kladně nabitá částice). Jeho pohyb bude zrychlený. Když ale vletí dovnitř, nebude na něj působit elektrické pole, protože prostor v duantu je proti elektrickému poli stíněn. Magnetické pole však není duantem odstíněno, takže deuteron se bude v duantu pohybovat po kruhové trajektorii, jejíž poloměr závisí na jeho rychlosti.
Během doby, kdy deuteron letí uvnitř záporně nabitého duantu, změní napětí mezi dvěma duanty svoji polaritu. Částice tedy bude mít před sebou opět záporně nabitý duant a bude znovu urychlována. Tento proces pokračuje, obíhající deuteron stále drží krok s oscilacemi napětí mezi duanty, dokud se nedostane po „spirálovité“ trajektorii k okraji duantu a nevyletí z cyklotronu.
Aby cyklotron takto úspěšně urychloval deuterony, musí být frekvence f, se kterou deuteron obíhá v magnetickém poli, rovna frekvenci fz elektrického zdroje. Má-li totiž energie obíhajícího protonu vzrůstat, musí být frekvence fz jednotlivých „postrčení“ deuteronu v mezeře mezi duanty rovna frekvenci, se kterou částice obíhá v magnetickém poli.
Jestliže nás zajímá, kolikrát proběhne deuteron mezi duanty v urychlovači, aby získal požadovanou energii, musíme si uvědomit, že při vstupu do středu cyklotronu má částice tak malou kinetickou energii, že ji můžeme zanedbat. Při každém urychlení získá energii úměrnou napětí mezi duanty.
Řešení a)
Deuterony s nábojem \(e\) vstupují do homogenního magnetického pole o magnetické indukci \(\vec{B}\) rychlostí \(\vec{v}\), která je kolmá k indukci \(\vec{B}\). Magnetická síla \(\vec{F}_\mathrm{m}\) působící na částici má velikost:
\[F_\mathrm{m}=evB.\]Při rovnoměrném pohybu po kružnici platí pro velikost dostředivé síly F:
\[F=ma=\frac{mv^2}{r}.\]Roli dostředivé síly \(\vec{F}\) hraje v našem případě magnetická síla \(\vec{F}_\mathrm{m}\), odkud pro její velikost dostáváme:
\[evB=\frac{mv^2}{r}.\]Z této rovnice můžeme vyjádřit poloměr kružnice, po níž se částice pohybuje:
\[r=\frac{mv}{eB}.\tag{1}\]Polovina periody \(\frac{T}{2}\) (tj, doba pro jeden oběh po půlkružnici) je rovna obvodu půlkružnice πr dělenému rychlostí částice v, takže:
\[\frac{T}{2}=\frac{\pi r}{v}=\frac{\pi}{v}\frac{mv} {eB}=\frac{\pi m}{eB}.\]Perioda oběhu T částice nezávisí na její rychlosti ani energii, takže doba mezi dvěma průlety částice mezi duanty je v průběhu urychlování pořád stejná.
Pro frekvenci f tedy platí:
\[f=\frac{1}{T}=\frac{eB}{2\pi m}.\]Aby cyklotron takto urychloval protony, musí být frekvence f, se kterou proton obíhá v magnetickém poli, rovna frekvenci fz zdroje napětí:
\[f_\mathrm{z}=f=\frac{eB}{2\pi m}.\]Náboj e je vždy konstantní. V nerelativistickém případě, jako je ten náš, je konstantní i hmotnost částice m. Zdroj napětí pracuje na jediné pevné frekvenci fz. Cyklotron potom ladíme pouze pomocí změn magnetického pole, dokud se neobjeví svazek urychlených protonů.
Řešení b)
Uvažujme, že na začátku měl deuteron zanedbatelně malou (téměř nulovou) kinetickou energii. Pro energii Ek, kterou částice s nábojem e získá při urychlení napětím U, platí:
\[E_\mathrm{k}=eU.\]Deuteron musí projít n-krát mezi duanty, aby dosáhl požadované energie Emax:
\[E_\mathrm{max}=nE_\mathrm{k}.\]Pro počet průchodů deuteronu mezi duanty tedy platí:
\[n=\frac{E_\mathrm{max}}{E_\mathrm{k}}=\frac{E_\mathrm{max}}{Ue}.\]Poloměr duantu R odpovídá poloměru kružnice Rmax při maximální energii částice. Velikost cyklotronu vyjádříme ze vztahu (1) pro poloměr kružnice (viz předchozí oddíl), po níž se částice pohybuje:
\[R_\mathrm{max}=\frac{mv}{eB}.\]Při maximální kinetické energii deuteronu se částice bude pohybovat rychlostí:
\[E_\mathrm{max}=\frac{1}{2}mv^2\,\,\,\,\Rightarrow\,\,\,\, v=\sqrt{\frac{2E_\mathrm{max}}{m}}.\]Pro poloměr duantu Rmax tedy platí:
\[R_\mathrm{max}=\frac{\sqrt{2mE_\mathrm{max}}}{eB}.\]Zápis a číselné dosazení
\(e\,\dot{=}\,1{,}6{\cdot} 10^{-19}\,\mathrm{C}\) náboj deuteronu \(m\,\dot{=}\,3{,}3 {\cdot} 10^{-27}\,\mathrm{kg}\) hmotnost deuteronu \(B=1{,}5\,\mathrm{T}\) velikost magnetického pole v urychlovači \(U = 50\,\mathrm{kV}\) rozdíl potenciálů mezi duanty \(E_\mathrm{max} = 16\,\mathrm{MeV}\,\dot{=}\,2{,}56{\cdot} 10^{-12}\,\mathrm{J}\) energie části při opuštění urychlovače \(f_\mathrm{z} =\,?\,\mathrm{(s^{-1})}\) frekvence zdroje napětí cyklotronu \(n=\,?\) počet proběhnutí deuteronu mezi duanty cyklotronu \(R=\,?\,\mathrm{(m)}\) poloměr cyklotronu
\[f_\mathrm{z}=\frac{eB}{2\pi m}=\frac{1{,}6{\cdot} 10^{-19}\cdot 1{,}5}{2\pi\cdot3{,}3 {\cdot} 10^{-27}}\dot{=} 11 {\cdot} 10^{6}\,\mathrm{s^{-1}}\] \[n=\frac{E_\mathrm{max}}{Ue}=\frac{2{,}56{\cdot} 10^{-12}}{50{\cdot} 10^{3}\cdot1{,}6{\cdot} 10^{-19}}=320\] \[R=\frac{\sqrt{2E_\mathrm{max}m}}{eB}=\frac{\sqrt{2{\cdot} 2{,}56{\cdot} 10^{-12}\cdot 3{,}3 {\cdot} 10^{-27}}}{1{,}6{\cdot} 10^{-19}\cdot 1{,}5}\,\mathrm{m}\dot{=}0{,}54\,\mathrm{m}=54\,\mathrm{cm}\]Odpověď
Zdroj elektrického pole má frekvenci přibližně 11·106 s-1. Deuteron proběhne mezi duanty 320krát, než dosáhne požadované hodnoty energie. Poloměr cyklotronu se rovná poloměru částice urychlené na požadovanou hodnotu energie. Tento poloměr je přibližně 54 cm.




