Sbírka řešených úloh

Výkon střídavého proudu v rezistoru

Úloha číslo: 162

• Nápověda 1

  Najděte si vzorec pro výkon v obvodu se stejnosměrným proudem. V obvodu se střídavým proudem se s časem mění jak proud, tak napětí, a tím i výkon. To znamená, že budeme porovnávat střední hodnotu výkonu v obvodu se střídavým proudem s výkonem v obvodu se stejnosměrným proudem.

• Nápověda 2

  Střední hodnota výkonu obvodu se střídavým proudem se má rovnat výkonu v obvodu s proudem stejnosměrným.

• Rozbor

  Tuto úlohu budeme řešit pomocí práce elektrického proudu. Mohli bychom ale rovnou porovnávat také střední hodnotu výkonu proudu v obvodu se střídavým proudem s výkonem proudu v obvodu se stejnosměrným proudem.

  Pro stejnosměrný proud vypočítáme práci jako součin tepelného výkonu rezistoru a času, během kterého daný rezistor koná práci.

  Ze zadání známe maximální hodnotu střídavého proudu, a proto vzorec pro vyjádření výkonu upravíme tak, aby v něm vystupoval tento proud a hodnota odporu rezistoru. Odpor rezistoru je pro oba obvody stejný. Pomocí grafu okamžitého výkonu určíme střední hodnotu výkonu a práci vykonanou za daný čas.

  Porovnáním vykonané práce v obvodu stejnosměrného a střídavého proudu získáme vztah mezi hodnotami obou proudů.

• Řešení - Odvození vztahu mezi efektivní hodnotou proudu a maximální hodnotou proudu

  Výkon na rezistoru v obvodu se stejnosměrným proudem popíšeme vztahem

  \[P=UI\mathrm{.}\]

  Tento vztah si pomocí Ohmova zákona \[U=IR\] přepíšeme do tvaru, kde bude vystupovat odpor rezistoru a proud:

  \[P=RI^2\mathrm{.}\]

   

  V obvodu se střídavým proudem se s časem mění proud i napětí, a tím i výkon, který je součinem obou předchozích veličin.

  Okamžitá hodnota výkonu v obvodu se střídavým proudem je vyjádřena vztahem

  \[p(t)=u\left(t\right)i\left(t\right).\]

  Máme-li v obvodu se střídavým proudem zařazen pouze rezistor, je fázový posun mezi proudem a napětím nulový. Platí tedy

  \[u\left(t\right)=R\,i\left(t\right).\]

  Vztah pro vyjádření okamžitého výkonu si můžeme přepsat do tvaru:

  \[p(t)=R \left[i\left(t\right)\right]^2.\]

   

  Celková práce za čas t je rovna ploše pod křivkou grafu p(t). Nejprve si to ukážeme na grafu výkonu pro stejnosměrný proud.

  

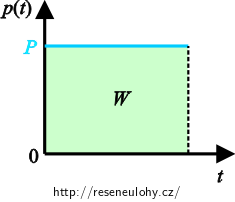
  V obvodu se stejnosměrným proudem je výkon konstantní a pro práci platí

  \[W=P\,t.\]

  Vidíme, že práce opravdu odpovídá ploše pod křivkou.

  Průběh okamžitého výkonu v obvodu se střídavým proudem je znázorněn na následujícím obrázku:

  

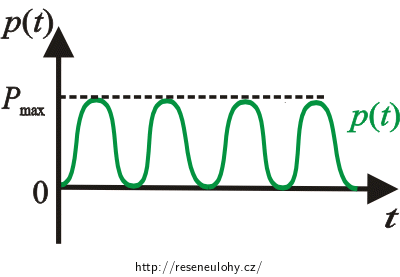
  Práci vypočítáme jako obsah plochy pod křivkou okamžitého výkonu p(t).

  

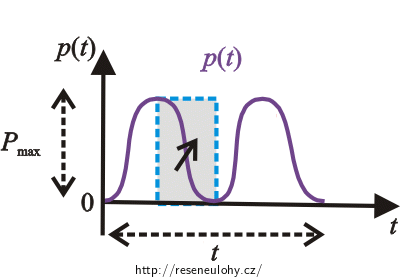
  Podíváme-li se na graf výkonu, vidíme, že křivka rozdělí znázorněný obdélníček na dvě stejně velké části. Proto střední hodnotu práce vypočteme jako:

  \[W=\frac{P_{\mathrm{max}}\,t}{2}.\]

  Platí, že maximální výkon vypočteme pomocí maximálního proudu

  \[P_{\mathrm{max}}=R\left(I_{\mathrm{max}}\right)^2\]

  a práci, kterou vykoná střídavý proud, dostaneme jako

  \[W=\frac{1}{2}R\left(I_{\mathrm{max}}\right)^2t.\]

   

  Stejnosměrný elektrický proud by za stejný čas vykonal práci:

  \[W=RI^2t.\]

   

  Porovnáme práci vykonanou stejnosměrným proudem s prací vykonanou v obvodu se střídavým proudem a získáme vztah mezi proudy v obou obvodech:

  \[\frac{1}{2}R\left(I_{\mathrm{max}}\right)^2t=R I^2 t,\] \[\frac{1}{2}\left(I_{\mathrm{max}}\right)^2=I^2,\] \[I=\frac{I_{\mathrm{max}}}{\sqrt2}.\]

• Poznámka k řešení

  Celkovou práci si můžeme představit jako součet obdélníčků pod křivkou, které mají výšku o velikosti výkonu p(t) a jsou široké malý časový interval Δt. Jejich součet bude roven ploše pod křivkou znázorňující okamžitý výkon. To se dá vyjádřit pomocí integrálu:

  \[W=\int_\mathrm{t}{p(t)}\,\mathrm{d}t.\]

• Číselné řešení

  Hodnota stejnosměrného proudu je

  \[I=\frac{I_{\mathrm{max}}}{\sqrt2}=\frac{3{,}5}{\sqrt2}\,\mathrm A\,\dot{=}\,2{,}5\,\mathrm A.\]

• Odpověď

  Stejnosměrný proud procházející daným rezistorem musí mít velikost asi 2,5 A, aby měl stejný tepelný výkon jako střídavý proud s maximální hodnotou 3,5 A.

• Komentář - Definice efektivní hodnoty střídavého proudu

  V této úloze jsme vlastně odvodili vztah mezi maximální a efektivní hodnotou střídavého proudu, protože efektivní hodnota střídavého proudu odpovídá (podle definice) hodnotě proudu stejnosměrného, který v daném obvodu vykoná za stejný čas (mnoho period) stejnou práci jako proud střídavý.

  Jinými slovy můžeme říci, že efektivní hodnota střídavého proudu odpovídá (podle definice) hodnotě proudu stejnosměrného, jehož výkon se rovná střední hodnotě výkonu v obvodu se střídavým proudem.