Nabitá obruč
Úloha číslo: 2004
V bodech na ose obruče o poloměru R, která je nabita nábojem s lineární hustotou \(\lambda\), určete přímou integrací
a) elektrickou intenzitu \(\vec{E}\),
b) potenciál \(\varphi\).
c) Ověřte platnost vztahu mezi \(\vec{E}\) a \(\varphi\).
Nápověda a)
Kladný bodový náboj Q vytváří v místě o vzdálenosti r pole o intenzitě
\[{E}=\frac{1}{4\pi\epsilon_0}\frac{Q}{r^2}.\]Vektor intenzity \(\vec{E}\) míří směrem od náboje, pokud je Q kladný. V opačném případě míří k náboji.
Zamyslete se nad tím, jak bychom tohoto poznatku mohli využít v této úloze.
Řešení a)
Bodový náboj Q vytváří ve vzdálenosti r pole o intenzitě
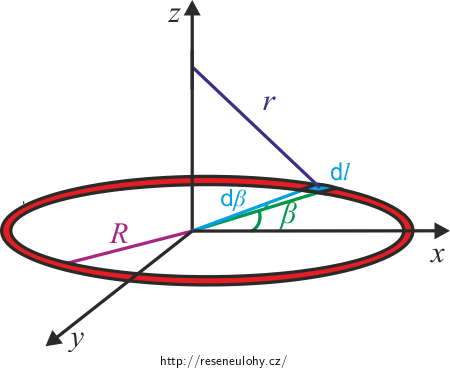
\[{E}=\frac{1}{4\pi\epsilon_0}\frac{Q}{r^2}.\]Je-li obruč nabita s lineární hustotou \(\lambda\), potom náboj dQ na nekonečně malém kousku obruče dl má velikost \[\textrm{d}Q = {\lambda} {\textrm{d}l},\]
kde \(\textrm{d}l=R \textrm{d}\beta\) (viz výpočet délky kruhového oblouku v radiánech).
Potom
\[\textrm{d}Q =\lambda R \textrm{d}\beta\]a tudíž
\[\textrm{d}{E}=\frac{1}{4\pi\epsilon_0} \frac{\textrm{d}Q}{r^2}=\frac{1}{4\pi\epsilon_0} \frac{\lambda R}{r^2}\textrm{d}\beta.\tag{1}\]Bez újmy na obecnosti můžeme předpokládat, že obruč je nabitá kladně. Nyní se zaměřme na směr výsledné intenzity. Využijeme souměrnost obruče.
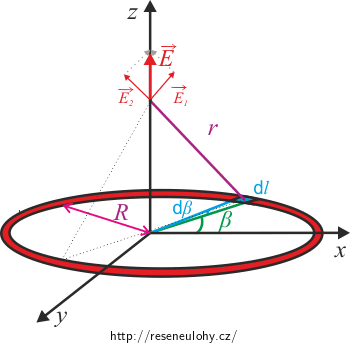
Z obrázku je patrné, že výsledný směr intenzity elektrického pole bude mít směr osy z, jelikož x–ová složka elektrické intenzity od malého kousku obruče se odečte s x–ovou složkou elektrické intenzity od malého kousku obruče, který je symetrický (středově souměrný) s tímto malým kouskem podle středu obruče. Stejně tak bude y–ová složka také nulová.
Pozn.: Pokud bychom si představili příspěvky k celkové intenzitě od všech kousků obruče, tak vyplní povrch kužele. Z toho je patrné, že jejich součet bude mířit ve směru osy obruče, tj. bude mít nenulovou pouze z–ovou složku.
Nyní se vrátíme k rovnici (1):
\[\textrm{d}{E}=\frac{1}{4\pi\epsilon_0}\frac{\lambda R}{r^2}\textrm{d}\beta.\]Do obrázku si zakreslíme úhel \(\alpha\) a elektrickou intenzitu promítneme do směru z, neboli vyjádříme její
z–ovou složku. Ostatní složky elektrické intenzity nás nemusí zajímat, jelikož z důvodu symetrie se vzájemně odečtou (viz výše).
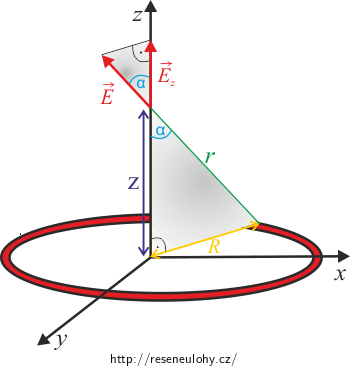
Je zřejmé, že
\[\textrm{d}E_\mathrm{z} = \cos \alpha\,\textrm{d}E.\tag{2}\]Pozn.: V tomto vztahu již vystupuje velikost intenzity \(E\) a velikost její složky \(E_\mathrm{z}.\)
Oba pravoúhlé trojúhelníky jsou podobné (mají stejné 2 úhly — pravý a \(\alpha\)), tudíž můžeme vyjádřit
\[\cos \alpha = \frac {z}{r}\]a z Pythagorovy věty víme, že
\[r^2 = R^2 + z^2,\]což nám dává
\[\cos \alpha = \frac{z}{\sqrt{R^2+z^2}}.\tag{3}\]Spojením (1), (2) a (3) dostaneme
\[dE_\mathrm{z}=\frac{1}{4\pi\epsilon_0} \frac{\lambda R}{z^2 + R^2}\frac{z}{\sqrt{ z^2 + R^2}} d\beta,\] \[dE_\mathrm{z}=\frac{\lambda R}{4\pi\epsilon_0} \frac {z} {\sqrt{(z^2 + R^2)^3}} d\beta,\]což zintegrujeme podél celého obvodu kružnice, tj. integrovat budeme přes úhel \(\beta\):
\[E_\mathrm{z} = \int_{0}^{2\pi}\frac{\lambda R}{4\pi\epsilon_0} \frac {z} {\sqrt{(z^2 + R^2)^3}} \textrm{d}\beta.\]Vzdálenosti R a z nezávisejí na úhlu \(\beta\), proto je můžeme z integrálu vytknout:
\[E_\mathrm{z} = \frac{\lambda R}{4\pi\epsilon_0} \frac {z} {\sqrt{(z^2 + R^2)^3}} \int_{0}^{2\pi} \textrm{d}\beta. \]Po zintegrování dostáváme
\[E_\mathrm{z} = \frac{\lambda R}{4\pi\epsilon_0} \frac {z} {\sqrt{(z^2 + R^2)^3}} {2\pi}, \] \[E_\mathrm{z} =\frac{\lambda R}{2\epsilon_0} \frac {z} {\sqrt{(z^2 + R^2)^3}}. \]Tedy
\[\vec{E}=\left(0,\ 0,\ \frac{\lambda R}{2\epsilon_0} \frac {z} {\sqrt{(z^2 + R^2)^3}}\right). \]Nápověda b)
Analogicky jako v části a) využijeme vztahu pro potenciál bodového náboje. Potenciál bodového náboje ve vzdálenosti r je
\[\varphi = k\frac{Q}{r}.\]Vymyslete, jak vztahu využít pro výpočet potenciálu na ose obruče.
Řešení b)
Bodový náboj Q vytváří ve vzdálenost r potenciál:
\[\varphi= k \frac {Q} {r}.\]Zaměříme-li se na jednu malou část obruče, pak potenciál od této části v daném místě na ose obruče je
\[\textrm{d}\varphi= k \frac {\textrm{d}Q} {r}\tag{4}\]a jelikož je obruč nabita s lineární hustotou \(\lambda\), pak
\[\textrm{d}Q=\lambda\textrm{d}l.\]Využijeme-li navíc poznatku \(\textrm{d}l=R\textrm{d}\beta\), pak dostaneme
\[\textrm{d}Q=\lambda R\textrm{d}\beta.\tag{5}\] \[\textrm{d}\varphi=k \frac {\lambda R}{r}\textrm{d}\beta. \tag{6}\]Nyní se zaměříme na vyjádření vzdálenosti r pomocí parametrů obruče a vzdálenosti z.
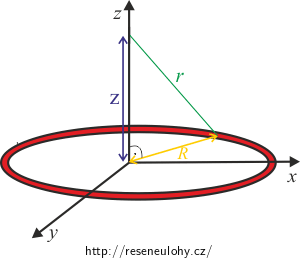
Z pravoúhlého trojúhelníku na obrázku vyjádříme r využitím Pythagorovy věty:
\[r=\sqrt{R^2 + z^2}.\tag{7}\] \[\textrm{d}\varphi=k \frac {\lambda R}{\sqrt{R^2 + z^2}}\textrm{d}\beta.\]Protože potenciál je skalární veličina, není třeba se zabývat jeho směrem a můžeme rovnou zintegrovat jednotlivé příspěvky:
\[\varphi=\int_{0}^{2\pi}k \frac {\lambda R}{\sqrt{R^2 + z^2}}\textrm{d}\beta,\] \[\varphi=k \frac {\lambda R}{\sqrt{R^2 + z^2}}\int_{0}^{2\pi}\textrm{d}\beta,\] \[\varphi=k \frac {\lambda R}{\sqrt{R^2 + z^2}}2\pi,\]tedy
\[\varphi=\frac {1}{2\epsilon_0} \frac {\lambda R}{\sqrt{R^2 + z^2}}.\]Nápověda c)
Potenciál a elektrickou intenzitu spojuje vztah, ve kterém vystupuje matematický operátor gradient.
Zkuste si vzpomenout, popřípadě najít, o jaký vztah se jedná. Připomeňte si, co gradient znamená a jak se počítá (v kartézských souřadnicích).
Řešení c)
Máme ověřit, zda platí vztah zmíněný v řešení nápovědy c), tj. vztah
\[\vec{E}=-\thinspace\text{grad}\thinspace\varphi.\]Ověření můžeme provést jen pro body na ose obruče a jen pro z–ovou složku, protože v části b) jsme určili pouze potenciál na ose z. Pro z–ovou složku elektrické intenzity v bodech osy obruče by mělo platit \(E_\mathrm{z}=-\frac{\partial{\varphi}}{\partial {z}}\). Spočtěme tedy uvedenou derivaci:
\[\frac{\partial{\varphi}}{\partial {z}}=\frac {\lambda R}{2\epsilon_0}(-1)\frac {1}{2} \frac {1}{\sqrt{(R^2 + z^2)^3}} 2z =-\frac {\lambda R}{2\epsilon_0} \frac {z}{\sqrt{(R^2 + z^2)^3}}. \]Tedy
\[E_\mathrm{z} = \frac {\lambda R}{2\epsilon_0} \frac {z}{\sqrt{(R^2 + z^2)^3}},\]což je stejný vztah, jaký nám vyšel přímou integrací v části a).
Nyní ještě ověříme, zda platí obrácený vztah
\[\varphi=-\int_\infty^{\hat {z}}{E_\mathrm{z}}\textrm{d}z.\]Dosadíme-li vypočítanou hodnotu \(E_\mathrm{z}\) z části a), dostaneme
\[\varphi=-\int_\infty^{\hat {z}}{\frac {\lambda R}{2\epsilon_0} \frac {z}{\sqrt{(R^2 + z^2)^3}}}\textrm{d}z.\]Konstanty vytkneme před integrál:
\[\varphi=-\frac {\lambda R}{2\epsilon_0} \int_\infty^{\hat {z}}{\frac {z}{\sqrt{(R^2 + z^2)^3}}}\textrm{d}z.\]Integrál budeme řešit pomocí substituce:
\[a = R^2 + z^2,\] \[\textrm{d}a =2z \textrm {d}z\]a přepočítáme meze:
\[z \rightarrow \infty \Rightarrow a \rightarrow \infty \qquad;\qquad z = \hat {z} \Rightarrow a = R^2 + \hat {z}^2.\] \[\varphi=-\frac {\lambda R}{2\epsilon_0} \int_\infty^{R^2 + \hat {z}^2} \frac {1}{2a^{3/2}}\textrm{d}a.\]Spočteme integrál
\[\varphi=\frac {\lambda R}{2\epsilon_0} \left[\frac {1}{a^{1/2}}\right]_\infty^{R^2 + \hat {z}^2}\]a dosadíme meze
\[\varphi=\frac {\lambda R}{2\epsilon_0} \frac {1}{(R^2 + \hat {z}^2)^{1/2}}.\]Jelikož \(\hat {z}\) je libovolný bod na ose z, můžeme napsat
\[\varphi=\frac {\lambda R}{2\epsilon_0} \frac {1}{(R^2 + {z}^2)^{1/2}},\]což je stejný vztah, jaký nám vyšel přímou integrací v části b).
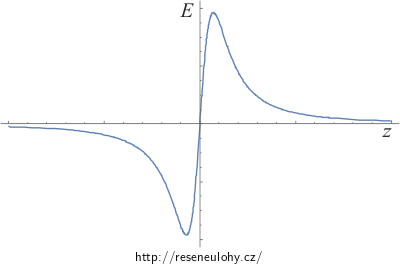
Grafy průběhu elektrické intenzity a potenciálu
Na následujících obrázcích si můžeme prohlédnout průběhy závislostí elektrické intenzity a potenciálu na vzdálenosti z od středu obruče.
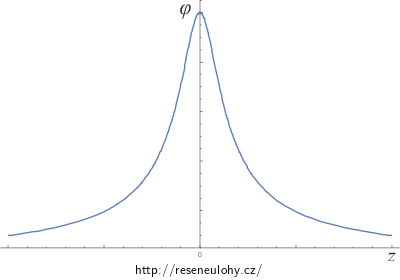
Odpověď
Velikost elektrické intenzity na ose homogenně nabité obruče je
\[{E}=\frac{\lambda R}{2\epsilon_0} \frac {z} {\sqrt{(z^2 + R^2)^3}},\]intenzita míří ve směru osy z.
Potenciál na ose homogenně nabité obruče má velikost \[\varphi=\frac {1}{2\epsilon_0} \frac {\lambda R}{\sqrt{R^2 + z^2}}.\]
Dále jsme pro body na ose obruče ověřili platnost vztahu mezi \(\vec {E}\) a \(\varphi\).
Analogická úloha
Analogickou úlohou je úloha Nabitá půlobruč.