Délka výboje doutnavky
Úloha číslo: 75
Ke zdroji střídavého napětí o efektivní hodnotě 230 V a frekvenci 50 Hz je připojena doutnavka. Doutnavka je do obvodu zapojena přes rezistor o hodnotě odporu 150 kΩ. Zápalné napětí doutnavky s rezistorem má hodnotu 116 V, zhášecí napětí má hodnotu 87 V. Určete dobu, po kterou doutnavka svítí v průběhu první poloviny periody.
Pozn.: Doutnavka popsaná v zadání je reálná doutnavka, kterou najdeme například ve vypínačích světla na chodbách budov.
Zápis
Ze zadání známe:
Napětí zdroje: U = 230 V Frekvence napětí zdroje: f = 50 Hz Odpor rezistoru: R = 150 kΩ Zápalné napětí doutnavky s rezistorem: UZ = 116 V Zhášecí napětí doutnavky s rezistorem: UZH = 87 V Chceme určit:
Dobu, po kterou doutnavka svítí: Δt = ? (s) Nápověda 1 - zápalné napětí
Doutnavka začne svítit, pokud napětí dosáhne zápalné hodnoty UZ = 116 V. Svítí v době, kdy je napětí vyšší než hodnota UZ. Jakmile hodnota napětí poklesne pod UZH = 87 V, doutnavka zhasne.
Nápověda 2
Uvědomte si, jaký průběh má střídavé harmonické napětí. Jak souvisí efektivní a maximální hodnota napětí?
Nápověda 3
Časový průběh napětí popíšeme pomocí funkce sinus:
\[u\left(t\right)=U_\mathrm{m} \sin{\left(\omega t\right)}.\]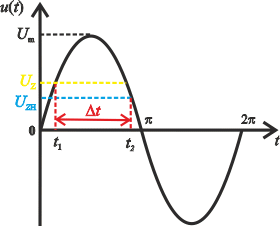
Rozbor úlohy
Doutnavka se rozsvítí, pokud napětí dosáhne hodnoty zápalného napětí, a zhasne, pokud napětí poklesne pod hodnotu zhášecího napětí. Naším úkolem je tedy najít interval mezi časem, ve kterém napětí přesáhne napětí zápalné, a časem, kdy napětí poklesne pod hodnotu zhášecího napětí. K tomu využijeme vyjádření časové závislosti napětí pomocí funkce sinus.
Řešení

Časová závislost střídavého napětí je obecně popsána vztahem:
\[u(t)=U_\mathrm{m}\, \sin(\omega t).\]Pro amplitudu napětí Um platí:
\[U_\mathrm{m}=\sqrt{2}U\mathrm{,}\]kde U je zadaná efektivní hodnota.
1) Zápalné napětí:
Hledáme okamžik, kdy se okamžité napětí v obvodu rovná zápalnému napětí doutnavky, tj. budeme řešit rovnici:
\[U_\mathrm{Z}=U_\mathrm{m}\, sin(\omega t_1),\] \[U_\mathrm{Z}=\sqrt{2}U\, sin(\omega t_1).\]Vyjádříme dobu, kdy se doutnavka rozsvítí:
\[\sin(\omega t_1)=\frac{U_\mathrm{Z}}{\sqrt{2} U}\] \[\omega t_1=\mathrm{arcsin} \left(\frac{U_\mathrm{Z}}{\sqrt{2} U}\right)\] \[t_1=\frac{\mathrm{arcsin} \left(\frac{U_\mathrm{Z}}{\sqrt{2} U}\right)}{\omega}.\]Pro výraz
\[\mathrm{arcsin} \left(\frac{U_\mathrm{Z}}{\sqrt{2} U}\right)\]dostaneme dvě číselné hodnoty:
a)\(\hspace{10px}\mathrm{arcsin} \left(\frac{U_\mathrm{Z}}{\sqrt{2} U}\right)=\mathrm{arcsin} \left(\frac{116}{\sqrt{2}\cdot 230}\right)=0{,}36,\)
b)\(\hspace{10px}\mathrm{arcsin} \left(\frac{U_\mathrm{Z}}{\sqrt{2} U}\right)=\mathrm{arcsin} \left(\frac{116}{\sqrt{2}\cdot 230}\right)=\pi - 0{,}36=2{,}78.\)
Z těchto dvou hodnot vybereme tu menší, tedy za a), protože ta odpovídá hodnotě t1 znázorněné na obrázku.
Číselně dosadíme do vyjádření doby, kdy se doutnavka rozsvítí:
\[t_{1}=\frac{\mathrm{arcsin} \left(\frac{U_\mathrm{Z}}{\sqrt{2} U}\right)}{\omega}=\frac{\mathrm{arcsin} \left(\frac{U_\mathrm{Z}}{\sqrt{2} U}\right)}{2 \pi f}=\frac{\mathrm{arcsin} \left(\frac{116}{\sqrt{2}\cdot 230}\right)}{2\pi\cdot 50}\,\dot{=}\,1{,}16\,\mathrm {ms}\]
Pozn.: Pokud Vám nevyšlo stejné číselné řešení, zkontrolujte, zda máte kalkulačku přepnutou na radiány. Pokud chcete počítat ve stupních, je nutné místo číslem 2π dělit výrazy pro čas hodnotou 360°.
2) Zhášecí napětí:
Hledáme okamžik, kdy se okamžité napětí v obvodu rovná zhášecímu napětí doutnavky, tj. budeme řešit rovnici:
\[U_\mathrm{ZH}= U_\mathrm{m} \, \sin(\omega t_2)\] \[U_\mathrm{ZH}=\sqrt{2} U \, \sin( \omega t_2).\]Vyjádříme dobu, kdy doutnavka zhasne:
\[\sin(\omega t_2)=\frac{U_\mathrm{ZH}}{\sqrt{2} U}\] \[\omega t_2=\mathrm{arcsin} \left(\frac{U_\mathrm{ZH}}{\sqrt{2} U}\right)\] \[t_2=\frac{\mathrm{arcsin} \left(\frac{U_\mathrm{ZH}}{\sqrt{2} U}\right)}{\omega}.\]Pro výraz \[\mathrm{arcsin} \left(\frac{U_\mathrm{ZH}}{\sqrt{2} U}\right)\] dostaneme dvě číselné hodnoty:
a)\(\hspace{10px}\mathrm{arcsin} \left(\frac{U_\mathrm{ZH}}{\sqrt{2} U}\right)=\mathrm{arcsin} \left(\frac{87}{\sqrt{2}\cdot 230}\right)=0{,}27,\)
b)\(\hspace{10px}\mathrm{arcsin} \left(\frac{U_\mathrm{ZH}}{\sqrt{2} U}\right)=\mathrm{arcsin} \left(\frac{87}{\sqrt{2}\cdot 230}\right)=\pi - 0{,}27=2{,}87.\)
Z těchto dvou hodnot vybereme tu větší, tedy za b), protože ta odpovídá hodnotě t2 znázorněné na obrázku.
Číselně dosadíme do vyjádření doby, kdy doutnavka zhasne:
\[t_{2}=\frac{\mathrm{arcsin} \left(\frac{U_\mathrm{ZH}}{\sqrt{2} U}\right)}{\omega}=\frac{\mathrm{arcsin} \left(\frac{U_\mathrm{ZH}}{\sqrt{2} U}\right)}{2 \pi f}=\frac{\mathrm{arcsin} \left(\frac{87}{\sqrt{2}\cdot 230}\right)}{2 \pi\cdot 50}\dot=9{,}14\,\mathrm {ms}.\]
Časový interval, ve kterém bude doutnavka svítit, získáme odečtením hodnot časů získaných z velikosti argumentu funkce sinus pro jednotlivá napětí:
\[ \Delta t = t_2 - t_1 = (9{,}14-1{,}16)\, \mathrm {ms} \,\dot{=}\,8\, \mathrm {ms}. \]Odpověď
Interval, ve kterém bude doutnavka svítit v průběhu jedné poloviny periody střídavého napětí, má délku 8 ms.
Komentář
Úlohu jsme řešili jen pro polovinu periody střídavého napětí. V průběhu celé periody doutnavka „blikne” dvakrát, protože svítí při obou směrech proudu.



