„Rozdělený“ RLC obvod
Úloha číslo: 74
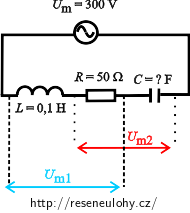
V obvodu střídavého proudu s frekvencí 50 Hz a amplitudou napětí 300 V je sériově zařazen kondenzátor neznámé kapacity, rezistor o odporu 50 Ω a cívka s indukčností 0,10 H. Poměr amplitud napětí ve dvou částech obvodu vyznačených na obrázku je Um1:Um2 = 1:2. Určete kapacitu kondenzátoru a amplitudu proudu protékající obvodem.
Zápis
Ze zadání známe:
Frekvenci obvodu f = 50 Hz Napětí na zdroji střídavého napětí Um = 300 V Odpor rezistoru v obvodu R = 50 Ω Indukčnost cívky v obvodu L = 0,10 H Poměr napětí vyznačených na obrázku: Um1:Um2 = 1:2 Chceme určit:
Kapacitu kondenzátoru: C = ? (F) Amplitudu proudu protékajícího obvodem: Im = ? (A) Nápověda 1
V sériovém RLC obvodu platí, že proud protékající jednotlivými prvky zařazenými v obvodu je stejný.
Nápověda 2
Části s vyznačenými napětími si můžeme představit jako dva samostatné obvody s daným celkovým napětím. Těmito obvody protéká stejný proud, protože ve skutečnosti jde o sériový RLC obvod.
Rozbor
V obvodu na obrázku v zadání úlohy jsme si pomyslně vybrali dvě části. Protože na nich „známe“ amplitudu napětí, můžeme každou část řešit zvlášť jako samostatný obvod. Použijeme Ohmův zákon pro střídavý proud. Oběma obvody protéká stejný proud. Z poměru napětí můžeme vyjádřit kapacitu.
Amplitudu proudu získáme pomocí Ohmova zákona, který aplikujeme na celý obvod.
Vyjádření napětí Um1 a Um2
V části obvodu, která náleží napětí Um1, je zapojena cívka o indukčnosti L a rezistor o odporu R. Cívka je s rezistorem spojena sériově.
Vyjádříme si impedanci Z1 této části obvodu:
\[ Z_1= \sqrt{R^2+(X_\mathrm{L}-X_\mathrm{C})^2}=\sqrt{R^2+X_\mathrm{L}^2}.\]Dosadíme ji do Ohmova zákona:
\[ U_\mathrm{m1}=I_\mathrm{m} Z_1=I_\mathrm{m}\sqrt{R^2+X_\mathrm{L}^2}=I_\mathrm{m} \sqrt{R^2+(\omega L)^2}. \]Pro část obvodu, kterému náleží hodnota napětí Um2, napíšeme podobné vztahy. V tomto obvodu máme sériově zapojen rezistor o odporu R a kondenzátor o neznámé kapacitě C:
\[ Z_2= \sqrt{R^2+(X_\mathrm{L}-X_\mathrm{C})^2}=\sqrt{R^2+X_\mathrm{C}^2}, \] \[ U_\mathrm{m2}=I_\mathrm{m} Z_2=I_\mathrm{m}\sqrt{R^2+X_\mathrm{C}^2}=I_\mathrm{m} \sqrt{R^2+\frac{1}{(\omega C)^2}}. \]Číselné dosazení
Kapacita v obvodu:
\[C=\frac{1}{\omega \sqrt{3R^2+4(\omega L)^2}}=\frac{1}{2 \pi \cdot 50 \sqrt{3{\cdot} 50^2+4(2 \pi\cdot 50{\cdot} 0{,}1)^2}}\,\mathrm{F} \,\dot{=}\, 30 {\cdot} 10^{-6} \,\mathrm{F}=30\,\mathrm{\mu F}.\]Amplituda proudu v obvodu:
\[I_\mathrm{m}=\frac{U_\mathrm{m}}{Z}=\frac{U_\mathrm{m}}{\sqrt{R^2+\left({\omega L-\frac{1}{\omega C}}\right)^2}}=\frac{300}{\sqrt{50^2+\left({2\pi\cdot 50 {\cdot} 0{,}1 - \frac{1}{2 \pi \cdot 50 {\cdot} 30\cdot 10^{-6}}}\right)^2}}\,\mathrm{A}\dot{=}\, 3{,}3 \,\mathrm{A}. \]Odpověď
Kapacita sériově zapojeného kondenzátoru je přibližně 30 μF.
Amplituda střídavého proudu v obvodu je asi 3,3 A.



