Drátěný čtverec

Úloha číslo: 27

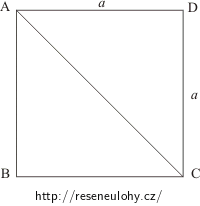
Určete elektrický odpor drátěného čtverce s úhlopříčkou pro dva případy:

a) čtverec je připojen ke zdroji napětí v bodech A, C,

b) čtverec je připojen ke zdroji napětí v bodech B, D.

Čtverec je zhotoven z homogenního drátu. Délku stran si označte a, průřez drátu S a měrný odpor ρ.

Nápověda 1
Do čtverce si „na dráty“ nakreslete rezistory o odpovídajícím odporu a zapojení si překreslete do „běžnější“ podoby. „Deformace“ obvodu nezmění jeho vlastnosti.
Řešení nápovědy 1
Odpory drátů na stranách čtverce a nahradíme rezistory o odpovídajícím odporu R_a. Odpor úhlopříčky nahradíme rezistorem, jehož odpor označíme R_c.

Tento obvod nyní můžeme překreslit do „běžnější“ podoby, podle toho, ve kterých bodech je obvod připojen ke zdroji napětí.

a) Čtverec je připojen v bodech A, C:

b) Čtverec je připojen v bodech B, D:
Nápověda 2
Uvědomte si, jak se počítá elektrický odpor homogenního drátu.
Řešení nápovědy 2
Elektrický odpor R homogenního drátu vypočítáme ze vztahu:
\[R\,=\,\rho\,\frac{l}{S}\,,\]
kde ρ je měrný odpor drátu, l jeho délka a S průřez drátu.
Rozbor
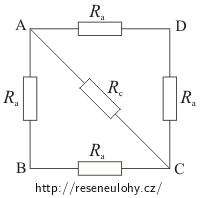
Aby se nám celá situace lépe představovala, doplníme si na každou úsečku rezistor o odpovídajícím odporu. V tomto novém schématu budeme jako obvykle předpokládat, že spojovací vodiče mají nulový odpor.

R_a odpovídá velikosti odporu drátu o délce a,

R_c odpovídá velikosti odporu drátu o délce c, kde c je úhlopříčka ve čtverci o straně a.

Obvod si překreslíme do „běžnější“ podoby podle toho, ve kterých bodech je připojen ke zdroji napětí.

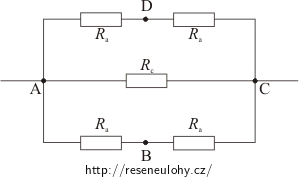
a) Čtverec je připojen v bodech A, C.

Využijeme toho, že při sériovém spojení rezistorů se celkový odpor rovná součtu odporů jednotlivých rezistorů. A pokud jsou rezistory řazeny paralelně, je převrácená hodnota celkového odporu rovna součtu převrácených hodnot odporů v jednotlivých větvích.

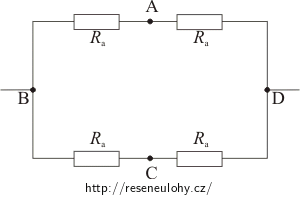
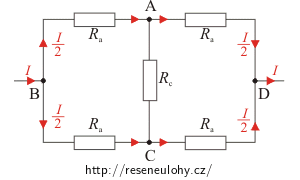
b) Čtverec je připojen v bodech B, D.

Představíme si, že do uzlu B vtéká proud I. Protože je obvod symetrický, rozdělí se tento proud na polovinu do obou větví. Z bodu D vytéká také proud I a díky symetrii zapojení můžeme opět říci, že proudy procházející větvemi CD a AD jsou stejné. Jejich velikost se rovná jedné polovině proudu I.

Z uzlu B do uzlu A přitéká proud \(\frac{I}{2}\), z uzlu A do D odtéká \(\frac{I}{2}\). Protože součet proudů vstupujících do uzlu se rovná součtu proudů vystupujících z uzlu, tak nezbývá žádný proud, který by protékal rezistorem R_c a můžeme ho tedy vynechat.

Při výpočtu celkového odporu využijeme stejné zákony jako v části a).
Řešení části a)
Jestliže je drátěný čtverec připojen ke zdroji napětí v bodech A, C, můžeme daný obvod překreslit takto:

kde \(R_\mathrm{a}\,=\, \rho\frac{a}{S} \), \(R_\mathrm{c}\,=\, \rho\frac{c}{S}\, \)

a c je velikost úhlopříčky ve čtverci o straně a, tedy
\[c\,=\,a \sqrt{2}\] \[R_\mathrm{c}\,=\, \rho\frac{a\sqrt{2}}{S}\,.\]
V našem případě to znamená, že celkový odpor vypočítáme z rovnice
\[\frac{1}{R}\,=\, \frac{1}{R_\mathrm{a}+R_\mathrm{a}}+\frac{1}{R_\mathrm{c}}+\frac{1}{R_\mathrm{a}+R_\mathrm{a}}\,.\]
Tuto rovnici upravíme:
\[\frac{1}{R}\,=\, \frac{1}{2R_\mathrm{a}}+\frac{1}{R_\mathrm{c}}+\frac{1}{2R_\mathrm{a}}\] \[\frac{1}{R}\,=\, \frac{2}{2R_\mathrm{a}}+\frac{1}{R_\mathrm{c}}\] \[\frac{1}{R}\,=\, \frac{R_\mathrm{c}+R_\mathrm{a}}{R_aR_\mathrm{c}}\,.\]
Pro celkový odpor tak získáme rovnici:
\[R\,=\, \frac{R_\mathrm{a}R_\mathrm{c}}{R_\mathrm{c}+R_\mathrm{a}}\,.\]
Nyní už jen dosadíme \(R_\mathrm{a}\,=\, \rho\frac{a}{S} \), \(R_\mathrm{c}\,=\, \rho\frac{a\sqrt{2}}{S}\,: \)
\[ R\,=\, \frac{\left(\rho\frac{a}{S}\right) \cdot \left(\rho \frac{a\sqrt{2}}{S}\right)}{\rho\frac{a\sqrt{2}}{S} +\rho\frac{a}{S} }\,=\, \frac {\sqrt{2}{\left(\rho\frac{a}{S}\right)}^2} {\left(\sqrt{2}+1\right)\rho\frac{a}{S}} \,=\, \frac{\sqrt{2}\rho\frac{a}{S}}{\left(\sqrt{2}+1\right)}\] \[R\,=\, \frac{\sqrt{2}}{\sqrt{2}+1}\cdot \rho\frac{a}{S} \hspace{20px}|\,\cdot \frac{\sqrt{2}-1}{\sqrt{2}-1}\] \[R\,=\, \frac{2-\sqrt{2}}{2-1}\cdot \rho\frac{a}{S}\,.\]
Výsledný vztah:
\[R\,=\, \left(2-\sqrt{2}\right) \rho\frac{a}{S}\,.\]
Řešení části b)
Jestliže je drátěný čtverec připojen ke zdroji v bodech B, D, můžeme obvod překreslit tímto způsobem:

Protože je zapojení symetrické, protéká větvemi BA, BC, AD i CD stejný proud. Rezistorem R_c tedy neprochází žádný proud. Tento rezistor neovlivňuje celkový odpor obvodu. Proto při řešení našeho obvodu můžeme větev s rezistorem R_c vynechat a dostaneme obvod:

Tím se nám celý obvod výrazně zjednodušil a můžeme dopočítat celkový odpor:
\[\frac{1}{R}\,=\, \frac{1}{\left(R_\mathrm{a}+R_\mathrm{a}\right)}+\frac{1}{\left(R_\mathrm{a}+R_\mathrm{a}\right)}\] \[\frac{1}{R}\,=\, \frac{1}{R_\mathrm{a}}\,.\]
Celkový odpor drátěného čtverce připojeného ke zdroji napětí v bodech C, D je:
\[R\,=\,R_\mathrm{a}\,,\]
kde R_a je elektrický odpor drátu o délce a:
\[R_\mathrm{a}\,=\, \rho\frac{a}{S}\,. \]
Odpověď
Pokud je drátěný čtverec připojen ke zdroji napětí v bodech A, C, je jeho celkový odpor \(R\,=\, \left(2-\sqrt{2}\right) \rho\frac{a}{S}\).

Jestliže čtverec připojíme ke zdroji napětí v bodech B, D, pak je jeho celkový odpor \(R\,=\, \rho\frac{a}{S}\).
Jiné možnosti jak řešit část b)
V případě, že bychom v části b) nepřišli na „fintu“ se stejnými proudy a možnost vynechat rezistor, kterým neprochází proud, pak bychom mohli tuto úlohu řešit např. pomocí Kirchhoffových zákonů (viz úloha Využití Kirchhoffových zákonů pro výpočet celkového odporu zapojení) nebo transformací trojúhelníku na hvězdu (viz úloha Transformace trojúhelník - hvězda). Stejně bychom museli postupovat i v případě, že bychom místo drátěného čtverce měli obdélník.

Další možností je řešení pomocí uzlů se stejným potenciálem. Jestliže mezi dvěma body obvodu neprochází proud (resp. by neprocházel, pokud bychom je propojili), znamená to, že mezi nimi není žádné napětí, tj. v obou bodech je stejný potenciál. Takové dva body v obvodu můžeme rozpojit nebo naopak propojit (sloučit do jednoho bodu), aniž bychom změnili celkový odpor zapojení.
Odkaz na podobnou úlohu
Podobná, ale obtížnější úloha pro výpočet celkového odporu obvodu je Odpor drátěné krychle. Tato úloha je řešena pomocí uzlů se stejným potenciálem.