Sbírka řešených úloh

Koeficient polarizovatelnosti

Úloha číslo: 185

Pokud se atom dostane do vnějšího elektrického pole, elektrony v obalu se mírně přeskupí, aby se dosáhlo nové rovnováhy. Přitom se z atomu stane dipól charakterizovaný dipólovým momentem

\[\vec p = \alpha \vec E,\]

kde α je koeficient atomové polarizovatelnosti. Ten závisí podstatným způsobem na struktuře daného atomu.

Jednoduchý model atomu sestává z bodového jádra s kladným nábojem +q a rovnoměrně rozprostřeného záporného náboje -q v objemu koule o poloměru a se středem v jádře. Vypočtěte koeficient polarizovatelnosti tohoto uspořádání.

Návod: Namísto přeskupení záporného náboje v obalu atomu uvažujte maličké posunutí jádra z jeho středu.

• Nápověda 1

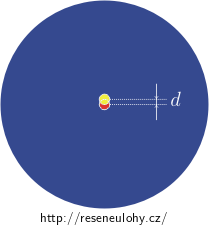
  Uvažte, že působením vnějšího pole se jádro maličko vychýlí ze středu koule. Toto vychýlení je natolik malé, že můžeme zanedbat změny ve struktuře rozložení záporného náboje (stále jej můžeme považovat za rovnoměrné).

  

• Nápověda 2

  Na vychýlené jádro bude působit nejen vnější pole o intenzitě \(\vec E\), ale nově také pole záporného náboje. Intenzitu pole záporného náboje označme \(\vec E_\mathrm{i}\). Při rovnoměrném rozložení záporného náboje ji lze určit například pomocí Gaussovy věty aplikované na kouli se středem ve středu atomu.

• Komentář k nápovědě 2

  Nabízí se přirozená otázka: proč předtím pole vyvolané záporným nábojem na jádro umístěné ve středu atomového obalu nepůsobilo? Můžeme nabídnout několik odpovědí:

  • Jednu odpověď nabízí symetrie: vezměme velmi malý kousek obalu a představme si ho jako záporný bodový náboj. Ten pochopitelně na jádro působí elektrickou silou. Můžeme ale k němu vždy najít středově symetrický stejný kousek, který bude na jádro působit elektrickou silou přesně opačnou.

    

  • Ještě jednu odpověď nabízí symetrie: předpokládejme, že na jádro elektrická síla od obalu působí. Potom ale musí mít nějaký směr. Celý atom nyní otočme kolem libovolné osy jdoucí středem atomu; tím se jakoby díváme z jiného úhlu pohledu a směr působící síly se změní. Avšak rozložení náboje se pootočením nezměnilo, a proto se nemohl změnit ani směr působící síly. To je spor.

    

  • Odpověď nabízí třeba také Gaussova věta elektrostatiky. Obal atomu si můžeme představit jako rovnoměrně nabité kulové slupky obepínající bodové jádro. Každá ze slupek ale ve svém vnitřku budí pole o nulové intenzitě. Integrací příspěvků od jednotlivých slupek docházíme k závěru, že intenzita elektrického pole vyvolaného obalem v jeho středu (nachází se uvnitř všech slupek) je nulová.

  • A konečně — pomocí Gaussovy věty elektrostatiky v příkladu průběh elektrické intenzity v obalu atomu spočítáme. Můžete se tedy podívat na vztah níže, kde dosadíte d = 0. Opět vám vyjde, že intenzita pole vyvolaného obalem atomu, je v jeho středu nulová.

• Rozbor

  Při působení vnějšího pole o intenzitě \(\vec E\) můžeme předpokládat, že se jádro „posune“ kousek ve směru orientace intenzity \(\vec E\). Toto posunutí je velmi malé, v prvním přiblížení tedy můžeme předpokládat, že záporný náboj (příliš) nezmění své rozmístění. Předpokládejme tedy, že zůstane přibližně rovnoměrně rozložený v dané kouli.

  Na kladné jádro posunuté o malou vzdálenost d ze středu rovnoměrně záporně nabité koule tak začne působit síla pole, které vytváří rovnoměrně rozložený záporný náboj. (Podívejte se na komentář k předchozí nápovědě, pokud vám není zřejmé, proč pole vytvářené obalem působí až na vychýlené jádro a nikoliv na jádro v jeho středu.)

  Podle Gaussovy věty, aplikované na kouli o poloměru d a středu totožným s centrem atomového obalu, má toto pole v místě jádra intenzitu stejnou jako pole bodového náboje, jehož velikost je rovna náboji obsaženému v kouli o poloměru d a umístěnému ve středu této koule.

  

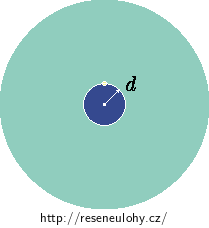
  Na jádro tedy působí dvě síly. Jedna od vnějšího pole, druhá od záporného náboje. V nové rovnováze se tyto dvě síly musí rovnat. Tak spočteme, do jaké vzdálenosti ze středu atomu se jádro vychýlí.

  Nakonec spočteme výsledný dipólový moment tohoto uspořádání. Pro účely tohoto výpočtu si můžeme představit, že veškerý záporný náboj je soustředěn ve středu koule. (Můžeme tak učinit z toho důvodu, že elektrické pole vně obalu (homogenně nabité koule) je stejné jako pole bodového náboje stejné velikosti, který je umístěn ve středu dané koule.) Proto dipólový moment můžeme vypočítat podle vztahu p = qd.

• Řešení

  Působením vnějšího pole se jádro maličko vychýlí ze středu atomu ve směru intenzity vnějšího pole \(\vec E\). Předpokládáme, že vychýlení je tak malé, že záporný náboj zůstane (přibližně) rovnoměrně rozložený v dané kouli.

  Řekněme, že nová rovnováha nastane ve chvíli, kdy se jádro dostane na vzdálenost \(d\ll R\) od středu záporně nabitého kulového oblaku. V tomto místě na něj působí pole tohoto oblaku o intenzitě E_i a podle Gaussovy věty platí

  \[E_\mathrm{i}\cdot 4\pi d^2 = \frac{q}{\varepsilon_0}\cdot\frac{\frac{4}{3}\pi d^3}{\frac{4}{3}\pi a^3},\]

  kde a je poloměr atomového obalu. Po úpravě dostáváme

  \[E_\mathrm{i} = \frac{1}{4\pi\varepsilon_0}\frac{qd}{a^3}.\]

  V rovnováze musí být obě síly působící na kladné jádro vyrovnány. Musí tedy nastat rovnost E = E_i, a proto:

  \[\alpha = \frac{p}{E} = \frac{p}{E_\mathrm{i}} = \frac{qd}{\frac{1}{4\pi\varepsilon_0}\frac{qd}{a^3}} = 4\pi\varepsilon_0a^3 = 3\varepsilon_0 V,\]

  kde V = 4/3πa³ je objem atomu.

• Pole rovnoměrně nabité koule

  Jak vypočítat intenzitu elektrického pole rovnoměrně nabité koule pomocí Gaussovy věty je podrobněji popsáno v úloze Pole rovnoměrně nabité koule.

• Komentář

  Pro atom vodíku je z experimentů určená hodnota koeficientu polarizovatelnosti přibližně \(\frac{\alpha}{4\pi\varepsilon_0}=0{,}667 {\cdot} 10^{-30}\,\mathrm{m^3}\), po úpravě \(\alpha\overset{\cdot}{=} 7{,}42{\cdot} 10^{-41} \ {\rm C}\,\cdot\,{\rm m}^{2}\,\cdot\, {\rm V}^{-1}.\)

  Zkusíme odtud ospravedlnit předpoklad, že posunutí jádra d je mnohem menší než poloměr atomového obalu a. Předpokládejme, že vnější pole má intenzitu E = 10⁵ V m^-1. Pro atom vodíku je q = e a jeho poloměr a uvažujeme zhruba 0,5 · 10^-10 m, a proto

  \[\frac{d}{a} = \frac{p}{qa} = \frac{\alpha E}{ea} = \frac{7{,}42\,\cdot\, 10^{-41}\,\cdot \,10^5}{1{,}6\,\cdot \,10^{-19}\,\cdot \,0{,}5\,\cdot \,10^{-10}} \overset{\cdot}{=} 10^{-6}.\]

• Výsledek

  Koeficient polarizovatelnosti tohoto uspořádání je \(3\varepsilon_0 V\), kde V je objem atomu.

• Odkaz na obtížnější úlohu

  Podobná, o něco obtížnější, je úloha Koeficient polarizovatelnosti atomu vodíku.