Pole nabité roviny řešené mnoha způsoby
Úloha číslo: 2132
Vypočtěte elektrickou intenzitu v okolí homogenně nabité nekonečné roviny (plošnou hustotu náboje označte \(\sigma\)):
a) přímou integrací za využití polárních souřadnic,
b) přímou integrací, rovinu uvažujte jako soustavu „mnoha přímek“ vedle sebe,
c) integrací potenciálu a užití vztahu mezi intenzitou a potenciálem,
d) pomocí Gaussovy věty elektrostatiky.
Pozn.: Předpokládejte, že rovina je nabita kladně.
a) Nápověda – přímá integrace pomocí polárních souřadnic
Kladný bodový náboj Q vytváří ve vzdálenosti r pole o velikosti intenzity
\[E=\frac{1}{4\pi\epsilon_0} \frac{Q}{r^2}.\]Vektor intenzity \(\vec{E}\) míří směrem od náboje, pokud je Q kladný. V opačném případě míří k náboji.
Zamyslete se nad tím, jak bychom tohoto poznatku mohli využít v této úloze.
a) Komentář – přímá integrace pomocí polárních souřadnic
Pro lepší představu si celou situaci nakreslíme do kartézských souřadnic. Do obrázku si vyznačíme také cylindrické souřadnice \(\rho, \alpha, z\).
Pozn.: Pro cylindrické souřadnice se standardně používá písmen r, \(\varphi\), z. Jelikož se písmenem \(\varphi\) označuje elektrický potenciál, s kterým budeme počítat, bylo nutné úhel označit jinak. Vzdálenost bodu od počátku soustavy souřadné obvykle značíme písmenem r, toto označení jsme nahradili písmenem \(\rho\), jelikož písmeno r vystupuje ve vzorci pro intenzitu bodového náboje. Pro shrnutí \(\rho\) je vzdálenost bodu od počátku soustavy souřadné a r je vzdálenost bodu od místa, v němž počítáme intenzitu elektrického pole (bod na ose z).
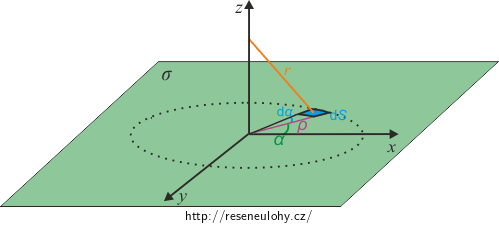
Dle nápovědy rozdělíme rovinu na malé (infinitezimální) plošky, které se budou chovat jako bodové náboje.
a) Řešení – přímá integrace pomocí polárních souřadnic
Bodový náboj Q vytváří ve vzdálenosti r pole o intenzitě
\[{E}=\frac{1}{4\pi\epsilon_0} \frac{Q}{r^2}.\]Velikost elektrické intenzity od infinitezimálně malé plošky dS je
\[\textrm{d}{E}=\frac{1}{4\pi\epsilon_0}\frac{\mathrm{d}Q}{r^2}.\]Je-li rovina nabita nábojem s plošnou hustotou \(\sigma\), potom náboj na infinitezimálně malém kousku roviny \(\textrm{d}S\) je
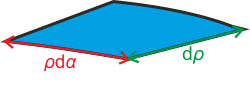
\[\textrm{d}Q = {\sigma} {\textrm{d}S},\]kde \(\textrm{d}S=\rho\,\textrm{d}\alpha\,\textrm{d}\rho\) (viz předchozí oddíl).
Potom dostáváme
\[\textrm{d}Q=\sigma \rho \textrm{d}\alpha\textrm{d}\rho\]a tudíž
\[\textrm{d}{E}=\frac{1}{4\pi\epsilon_0}\frac{\sigma \rho\textrm{d}\alpha\textrm{d}\rho}{r^2}.\tag{1}\]Nyní se zaměříme na směr intenzity. Víme, že jde o nekonečnou rovinu, která je homogenně nabitá.
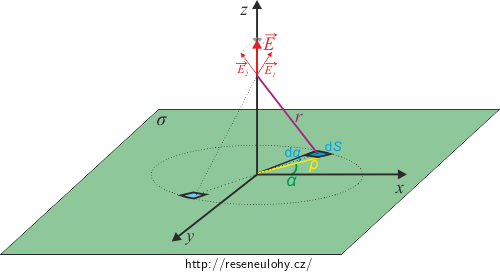
Z obrázku je patrné, že směr celkové intenzity elektrického pole bude mít směr osy z, jelikož x–ová složka elektrické intenzity od nějaké konkrétní plošky roviny se odečte s x–ovou složkou elektrické intenzity plošky, která je symetrická (středově souměrná) s touto ploškou podle počátku souřadného systému. Stejně tak bude y–ová složka celkové intenzity také nulová.
V obrázku si označíme úhel \(\omega\) a elektrickou intenzitu od jedné malé plošky promítneme do směru z, neboli vyjádříme její z–ovou složku:
\[E_\mathrm{z}=E \cos \omega.\tag{2}\]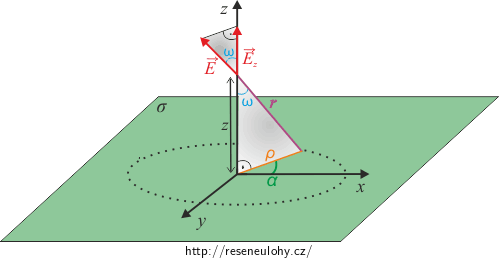
Z pravoúhlosti spodního šedého trojúhelníku dostaneme
\[\cos \omega = \frac {z}{r}\]a Pythagorova věta nám k tomu přidá
\[r=\sqrt{\rho^2 + z^2},\]což dává
\[\cos \omega = \frac {z}{\sqrt{\rho^2 + z^2}}.\tag{3}\]Spojením (1),(2) a (3) dostaneme
\[\textrm{d}{E_\mathrm{z}}=\frac{1}{4\pi\epsilon_0}\frac{\sigma\rho \textrm{d}\alpha\textrm{d}\rho}{\rho^2 + z^2}\frac {z}{\sqrt{\rho^2 + z^2}}=\frac {\sigma z}{4\pi\epsilon_0} \frac {\rho} {(\rho^2 + z^2)^{3/2}} \textrm{d}\alpha \textrm{d}\rho,\]což zintegrujeme přes celou rovinu, tj. budeme integrovat přes \(\rho\) a \(\alpha\), \(\rho\) nabývá hodnot od \(0\) do \(\infty\) a \(\alpha\) nabývá hodnot od \(0\) do \(2\pi\):
\[E_\mathrm{z} = \int_0^\infty \int_0^{2\pi} \frac {\sigma z}{4\pi\epsilon_0} \frac {\rho} {(\rho^2 + z^2)^{3/2}} \textrm{d}\alpha \textrm{d}\rho.\]Veličiny \(\sigma\) a z jsou nezávislé na integračních proměnných \( \rho \) a \(\alpha,\) tudíž je můžeme s ostatními konstantami vytknout před integrál:
\[E_\mathrm{z} = \frac {\sigma z}{4\pi\epsilon_0} \int_0^\infty \int_0^{2\pi} \frac {\rho} {(\rho^2 + z^2)^{3/2}}\textrm{d}\alpha \textrm{d}\rho .\]Nyní výraz zintegrujeme přes proměnou \(\alpha\), jelikož se ve výrazu \(\alpha\) nevyskytuje, integrujeme vlastně konstantu:
\[E_\mathrm{z} =\frac {\sigma z}{4\pi\epsilon_0} 2\pi \int_0^\infty \frac {\rho} {(\rho^2 + z^2)^{3/2}}\textrm{d}\rho,\] \[E_\mathrm{z} = \frac {\sigma z}{2\epsilon_0} \int_0^\infty \frac {\rho} {(\rho^2 + z^2)^{3/2}}\textrm{d}\rho.\]Zbývající integrál přes \(\rho\) budeme řešit substitucí:
\[a = \rho^2 + z^2,\] \[\textrm{d}a = 2\rho\textrm{d}\rho, \]přepočítáme meze:
\[\rho = 0 \Rightarrow a = z^2;\qquad \rho = \infty \Rightarrow a = \infty, \]a dosadíme do původního integrálu:
\[E_\mathrm{z} = \frac {\sigma z}{2\epsilon_0} \int_{z^2}^{\infty} \frac {1} {2a^{3/2}}\textrm{d}a,\] \[E_\mathrm{z} = \frac {\sigma z}{4\epsilon_0} \int_{z^2}^{\infty} {a^{-3/2}}\textrm{d}a,\] \[E_\mathrm{z} = \frac {\sigma z}{4\epsilon_0} \left[-2a^{-1/2}\right]_{z^2}^\infty, \] \[E_\mathrm{z} = - 0 + \frac {\sigma}{2\epsilon_0}\frac{z}{|z|}=\frac {\sigma}{2\epsilon_0}\frac{z}{|z|}. \]Poslední zlomek ve výsledku je jednotkový vektor rovnoběžný s osou z, který určuje směr elektrické intenzity. Pokud by rovina byla nabita kladně, pak elektrická intenzita míří ve směru kladné osy z, pokud jsme nad rovinou, a elektrická intenzita míří ve směru záporné osy z, pokud jsme pod rovinou.
b) Nápověda – přímá integrace pomocí „mnoha přímek“
Homogenně nabitá přímka s lineární hustotou náboje \(\lambda\) vytváří kolem sebe pole o velikosti (viz Pole nabité přímky)
\[E = \frac {\lambda}{2\pi\epsilon_0z.}\]Elektrická intenzita míří kolmo od vodiče a její směr je zobrazen na následujícím obrázku.
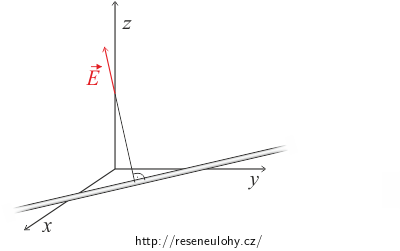
Zamyslete se nad tím, jak bychom tohoto poznatku mohli využít.
b) Rozbor – přímá integrace pomocí „mnoha přímek“
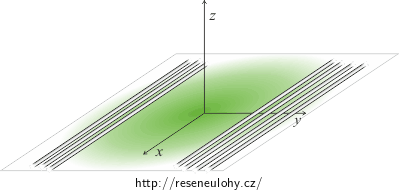
Rovinu si rozdělíme na nekonečně mnoho navzájem rovnoběžných přímek. Celkovou intenzitu získáme „sečtením“ (přesněji integrováním) příspěvků od všech těchto malých kousků.
b) Řešení – přímá integrace pomocí „mnoha přímek“
Zvolme si kartézskou soustavu souřadnou tak, že nabitá rovina leží v rovině xy a my hledáme elektrickou intenzitu na ose z.
Víme, že homogenně nabitá přímka s lineární hustotou \(\lambda\) vytváří ve vzdálenosti r elektrické pole o velikosti
\[E=\frac{\lambda}{2\pi\epsilon_0r}.\tag{4}\]Viz Pole nabité přímky.
Lineární hustota \(\lambda\) souvisí s plošnou hustotou \(\sigma\) vztahem
\[\lambda = \sigma\ \mathrm{d}y.\]Pokud si představíme rovinu jako velmi mnoho navzájem rovnoběžných přímek, pak příspěvek k intenzitě elektrického pole od jedné přímky je
\[dE=\frac{\sigma}{2\pi\epsilon_0r}\textrm{d}y.\]Zamysleme se nad symetrií úlohy.
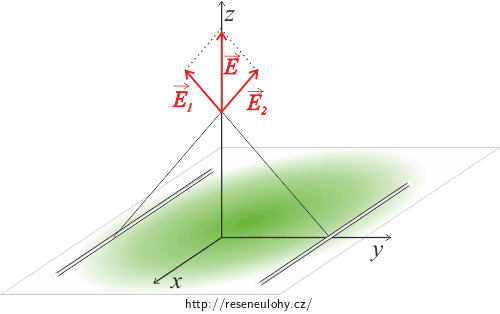
Z obrázku je vidět, že ke každé přímce existuje přímka s ní symetrická podle námi zvolené kartézské osy x. Všechny příspěvky mají nulovou x–vou složku, příspěvky k y–ové složce elektrické intenzity od symetricky umístěných přímek se navzájem odečtou a nenulová zůstane pouze z–ová složka.
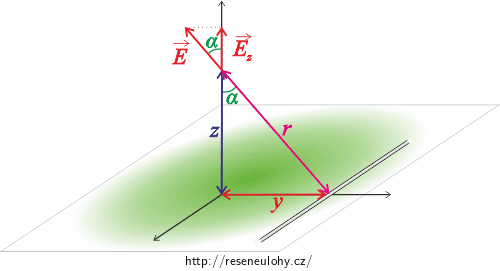
V obrázku si označíme úhel \(\alpha\) a elektrickou intenzitu od jedné přímky promítneme do směru z, neboli vyjádříme její z-ovou složku:
\[E_\mathrm{z} = \cos \alpha \ E.\tag{5}\]Z podobnosti pravoúhlých trojúhelníků dostaneme
\[\cos \alpha = \frac {z}{r},\]kde \(r=\sqrt{z^2 + y^2}.\)
\[\textrm {d}E_\mathrm{z} = \frac {z}{\sqrt{z^2+y^2}}\frac{\sigma}{2\pi\epsilon_0\sqrt{z^2+y^2}}\textrm{d}y,\]což zintegrujeme přes všechny přímky, tj. budeme integrovat přes \(y\):
\[E_\mathrm{z} = \int_{-\infty}^{\infty}\frac{\sigma z}{2\pi\epsilon_0{(z^2+y^2)}}\textrm{d}y,\] \[E_\mathrm{z} = \frac{\sigma z}{2\pi\epsilon_0}\int_{-\infty}^{\infty}\frac{1}{z^2+y^2}\textrm{d}y.\]Tento integrál vede na funkci arkustangens (funkce inverzní k funkci tangens). Připomeneme si derivaci funkce arkustangens
\[\frac{\mathrm{d}\ \mathrm{arctg}\, x}{\mathrm{d}x}=\frac{1}{1+x^2}\]a integrál, jejž počítáme, upravíme na takový tvar, abychom vzorec mohli použít. Z jmenovatele integrálu vytkneme \(z^2\):
\[E_\mathrm{z} = \frac{\sigma }{2\pi\epsilon_0 z} \int_{-\infty}^{\infty}\frac{1}{1+(\frac{y}{z})^2}\textrm{d}y,\] \[E_\mathrm{z} = \frac{\sigma }{2\pi\epsilon_0 z} \Big[z\arctan\frac{y}{z}\Big]_{-\infty}^{\infty}.\]O funkci arkustangens víme
\[\lim_{y\rightarrow \pm\infty}\arctan{\frac{y}{z}}=\pm\frac{\pi}{2} \mathrm{sgn}\ z=\pm\frac{\pi}{2} \frac {z}{|z|},\]což po dosazení dává
\[E_\mathrm{z} = \frac{\sigma }{2\pi\epsilon_0 z}(z \frac {|z|}{z} \frac{\pi}{2} + z \frac {|z|}{z} \frac{\pi}{2}),\] \[E_\mathrm{z} = \frac{\sigma }{2\epsilon_0} \frac {|z|}{z}.\]Pozn.: Funkce \(\mathrm{sgn}\ x\), které říkáme signum, je funkce, která vrací znaménko proměnné, tedy je-li \(x>0\), pak \(\mathrm{sgn}\ x=1\), je-li \(0>x\), pak \(\mathrm{sgn}\ x=-1\), a pro \(x=0\) je \(\mathrm{sgn}\ x = \mathrm{sgn}\ 0=0\).
c) Nápověda – intenzita z potenciálu
Potenciál a elektrickou intenzitu nám dává do vztahu jedna z rovností, ve které vystupuje matematický operátor gradient.
Zkuste si vzpomenout, popřípadě najít, o jaký vztah se jedná. Připomeňte si, co gradient znamená a jak se počítá (v kartézských souřadnicích).
Dále zkuste najít, jaký je potenciál nad rovnoměrně nabitou rovinou s plošnou hustotou \(\sigma.\)
c) Nápověda – vztah pro potenciál v okolí nabité roviny
Potenciál elektrického pole homogenně nabité roviny má tvar (viz Potenciál rovnoměrně nabité roviny)
\[\varphi(z) = - \frac {\sigma}{2\epsilon_0} |z|.\]c) Řešení – intenzita z potenciálu
Elektrická intenzita a potenciál elektrického pole jsou spjaty rovností
\[\vec{E} = - \text{grad} \varphi = -\left(\frac{\partial{\varphi}}{\partial {x}},\frac{\partial{\varphi}}{\partial {y}},\frac{\partial{\varphi}}{\partial {z}}\right).\]Pravá strana rovnosti nám říká, jak se počítá gradient ze skalární funkce v kartézských souřadnicích:
\[\varphi(x,y,z) = - \frac {\sigma}{2\epsilon_0} |z|.\]Pozn.: V tomto případě známe závislost potenciálu na všech souřadnicích (máme ho vyjádřený ve všech bodech), tudíž můžeme počítat všechny složky elektrické intenzity. Jinak tomu bylo u výpočtu na ose homogenně nabité obruče, viz Elektrické pole na ose obruče, i když se může zdát, že se jedná o podobný případ.
Výpočet prvních dvou složek intenzity je jednoduchý:
\[\frac{\partial{\varphi}}{\partial {x}}=0,\] \[\frac{\partial{\varphi}}{\partial {y}}=0.\]Při výpočtu z–ové složky, tj. při derivování výrazu pro potenciál podle z, si kvůli absolutní hodnotě rozdělíme příklad na dvě části. Derivaci budeme počítat zvlášť pro \(z>0\) a pro \(z<0\).
Pro \(z>0\) bude mít potenciál v okolí nabité roviny tvar
\[\varphi(x,y,z) = - \frac {\sigma}{2\epsilon_0} z,\]po zderivování dostaneme
\[\frac{\partial{\varphi}}{\partial {z}}= -\frac {\sigma}{2\epsilon_0} \qquad \text{pro}\ \forall z>0.\]Pro \(z<0\) bude mít potenciál v okolí nabité roviny tvar
\[\varphi(x,y,z) = - \frac {\sigma}{2\epsilon_0} (-z) = \frac {\sigma}{2\epsilon_0} z,\]po zderivování dostaneme
\[\frac{\partial{\varphi}}{\partial {z}}= \frac {\sigma}{2\epsilon_0} \qquad \text{pro}\ \forall z<0.\]Oba výsledky můžeme propojit a zapsat v jednom výrazu:
\[\frac{\partial{\varphi}}{\partial {z}}= -\frac {\sigma}{2\epsilon_0}\frac{z}{|z|} \qquad \text{pro}\ \forall z \in \mathbb{R} \setminus \text{{0}}.\]Pro elektrickou intenzitu tedy dostáváme vztah
\[\vec{E} = \left(0, 0, \frac {\sigma}{2\epsilon_0}\frac{z}{|z|} \right), \qquad \text{pro}\ \forall z \in \mathbb{R} \setminus \text{{0}}. \]Stejně jako v a) a b) je poslední zlomek ve výsledku jednotkový vektor rovnoběžný s osou z, který určuje směr elektrické intenzity. Pokud by rovina byla nabita kladně, pak elektrická intenzita míří ve směru kladné osy z, pokud jsem nad rovinou, a elektrická intenzita míří ve směru záporné osy z, pokud jsem pod rovinou.
d) Odkaz – pomocí Gaussovy věty elektrostatiky
Výpočet elektrostatické intenzity v okolí homogenně nabité roviny pomocí Gaussovy věty elektrostatiky je řešen v úloze Pole rovnoměrně nabité roviny.
Odpověď
Vektor elektrické intenzity v okolí homogenně nabité nekonečné roviny má tvar
\[\vec{E}=\left(0\ ; 0\ ; \frac {\sigma}{2\epsilon_0}\frac{z}{|z|} \right).\]