Urychlená α částice
Úloha číslo: 56
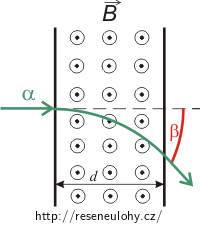
Částice α byla urychlena z klidu elektrickým polem s rozdílem potenciálů 250 kV a vlétla do homogenního magnetického pole o magnetické indukci 0,51 T kolmo k indukčním čarám. Šířka oblasti magnetického pole je 10 cm (viz obrázek). Určete úhel, o který se částice odchýlí od původního směru.
Pozn.: Částice α má dvojnásobný náboj a přibližně čtyřnásobnou hmotnost ve srovnání s protonem.
Nápověda 1
Uvědomte si:
- jakou bude mít částice energii a rychlost po průchodu elektrickým polem;
- jaké síly působí na částici v homogenním magnetickém poli;
- jak se změní její trajektorie v důsledku těchto sil.
Nápověda 2
Magnetická síla je kolmá na pohyb a působí jako síla dostředivá. Částice α se bude tedy pohybovat po kružnici.
Rozbor
Na částici α pohybující se v magnetickém poli působí kolmo ke směru jejího pohybu magnetická síla. Sílu kolmou na směr pohybu nazýváme dostředivá síla a tato síla uděluje částici dostředivé zrychlení. Trajektorie částice α se proto v homogenním magnetickém poli zakřiví a bude mít tvar části kružnice. Velikost rychlosti částice α se při pohybu v magnetickém poli nebude měnit.
Pro výpočet magnetické síly potřebujeme znát rychlost částice α, se kterou vlétla do magnetického pole. Tu vypočítáme pomocí práce elektrických sil při jejím urychlování. Protože částice α byla na začátku v klidu, bude tato práce rovna kinetické energii částice α po urychlení.
Obrázek
Řešení
Nejprve pomocí energií určíme rychlost v částice α v magnetickém poli.
Částice α s nábojem Qα = 2e byla urychlena elektrickým polem s napětím U. Elektrické síly vykonaly práci W = QαU. To se projevilo zrychlením, tedy zvýšením kinetické energie částice o stejnou hodnotu. Před urychlováním byla částice v klidu, proto můžeme napsat, že vykonaná práce se rovná kinetické energii částice α po urychlení.
\[W=E_\mathrm{k}\] \[Q_\alpha U=\frac{1}{2}m_\alpha v^{2}\] \[2eU=\frac{1}{2}\cdot 4 m_\mathrm{p} v^{2}\] \[eU=m_\mathrm{p} v^{2}\]Odtud vyjádříme rychlost částice α
\[v=\sqrt{\frac{e U}{m_\mathrm{p}}}.\]Na částici α pohybující se v magnetickém poli kolmo k indukčním čarám působí magnetická síla Fm o velikosti
\[F_m = Q_\alpha vB.\]Magnetická síla působí kolmo ke směru jejího pohybu, a proto působí jako síla dostředivá
\[F_\mathrm{d} =m_\alpha a_\mathrm{d}, \]kde dostředivé zrychlení ad vyjádříme pomocí velikosti rychlosti
\[a_\mathrm{d} = \frac{v^{2}}{r}.\]Porovnáme vyjádření dostředivé a magnetické síly
\[F_\mathrm{d}=F_\mathrm{m}\] \[m_\alpha\frac{v^{2}}{r} = Q_\alpha vB\] \[4m_\mathrm{p}\frac{v^{2}}{r} = 2evB\]a vyjádříme neznámý poloměr r
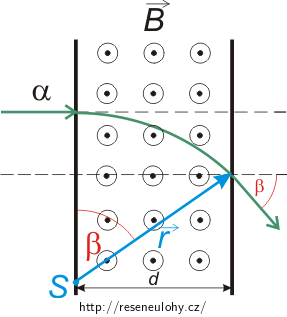
\[r = \frac{2m_\mathrm{p}v}{Be}=\frac{2}{B}\,\sqrt{\frac{m_\mathrm{p}U}{e}}.\]Z obrázku vyplývá, že pro hledaný úhel β platí
\[\sin\beta = \frac{d}{r},\]kam za poloměr r dosadíme a dostáváme
\[\sin\beta = \frac{Bd}{2}\,\sqrt{\frac{e}{m_\mathrm{p} U}}.\]Zápis a číselné dosazení
\(Q_\alpha = 2\, e\) náboj částice \(m_\alpha = 4 \,m_\mathrm{p}\) hmotnost částice \(U = 250\,\mathrm{kV}\) rozdíl potenciálů pole \(B=0{,}51\,\mathrm{T}\) magnetická indukce pole \(d=0{,}10\,\mathrm{m}\) šířka oblasti magnetického pole \(\beta=\mathrm{?}\,\mathrm{(^\circ)}\) úhel odchýlení částice Z tabulek: \(e \approx 1{,}6{\cdot} 10^{-19}\,\mathrm{C}\) náboj protonu \(m_\mathrm{p} \approx 1{,}67 {\cdot} 10^{-27}\,\mathrm{kg}\) hmotnost protonu
Výpočet rychlosti:
\[v=\sqrt{\frac{Q_pU}{m_\mathrm{p}}}=\sqrt{\frac{2{\cdot}1{,}6{\cdot}10^{-19}\cdot250{\cdot}10^{3}}{1{,}67{\cdot}10^{-27}}}\,\mathrm{m\,s^{-1}}\dot{=}\,6{,}92{\cdot}10^{6} \,\mathrm{m\,s^{-1}}.\]Výpočet úhlu, o který se α částice odchýlí od původního směru:
\[\sin\beta = \frac{Bd}{2}\,\sqrt{\frac{e}{m_\mathrm{p} U}} = \frac{0{,}51{\cdot}0{,}1}{2}\,\cdot\,\sqrt{\frac{1{,}6{\cdot}10^{-19}}{1{,}67 {\cdot} 10^{-27}\cdot250{\cdot}10^{3}}}\,\dot{=}\, 0{,}50\] \[\beta \,\dot{=}\, 30^{\circ}.\]Odpověď
Částice α se od původního směru v homogenním magnetickém poli odchýlila asi o 30°.
Dynamický prvek
Následující aplet zobrazuje částici \(\alpha\) nalétávající do magnetické pole. Pomocí posuvníků můžete nastavit parametry apletu jako je šířka oblasti s magnetickým polem \(d\), urychlující napětí \(U\) a velikost magnetické indukce \(B\). Pomocí tlačítek můžete zapínat a vypínat zobrazení pohybu částice a také vymazat zobrazené trajektorie.
Pozn.: Neměňte parametry v průběhu letu částice, aplet by vykresloval nefyzikální chování.
Úlohy pro práci s apletem:
Nejprve si rozmyslete řešení následujících úkolů a správnost svého úsudku si potom ověřte pomocí apletu.
-
Chceme zmenšit úhel odchýlení tím, že zvětšíme hodnotu právě jednoho z parametrů. Je více možností, který parametr zvětšit?
Chceme zmenšit úhel odchýlení tím, že zmenšíme hodnotu právě jednoho z parametrů. Je více možností, který parametr zmenšit?
Parametry apletu nastavte na \(d=0{,}1\space \mathrm{cm},\space U=100\space \mathrm{V}, \space B=0{,}7\space \mathrm{T}.\) Spusťte aplet a pozorujte, co se stane. Pro každou veličinu, jejíž hodnotu můžete nastavit, určete, jak ji změnit (zatímco ostatní zůstanou nezměněné), aby částice doletěla na konec magnetického pole. Své řešení si zkontrolujte pomocí apletu.
-



