Sbírka řešených úloh

Síla působící na desky kondenzátoru

Úloha číslo: 38

• Obrázek

  

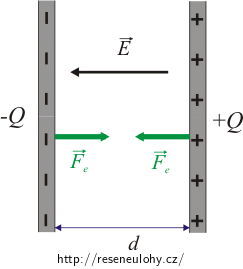
• Nápověda: Intenzita pole

  Intenzita homogenního pole mezi deskami je dána napětím mezi nimi a jejich vzdáleností. Obě desky přispívají do této intenzity stejně.

• Nápověda: Velikost síly

  Síla, kterou působí jedna deska kondenzátoru na druhou, závisí na náboji první desky a na velikosti intenzity elektrického pole, které vytváří pouze druhá deska.

• Rozbor: Síla působící na desky kondenzátoru

  Na obou deskách kondenzátoru je rovnoměrně rozložen náboj Q. Na jedné desce je náboj kladný, na druhé záporný, proto se desky přitahují elektrickou silou.

  Síla působící na první desku je úměrná velikosti náboje na této desce a intenzitě elektrického pole, které vytváří druhá deska (první deska sama na sebe nepůsobí).

  Intenzita homogenního pole kondenzátoru je dána vektorovým součtem intenzit polí od obou desek. Znaménko náboje desky ovlivňuje to, zda intenzita míří k desce, nebo od ní. Mezi deskami oba vektory míří stejným směrem a mimo kondenzátor se navzájem ruší. Intenzita pole od jedné desky bude tedy poloviční než celková intenzita pole uvnitř kondenzátoru.

  

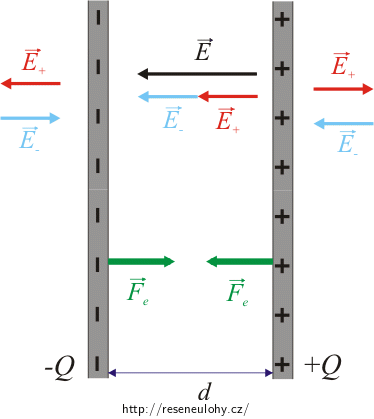
• Řešení: Síla působící na desku kondenzátoru

  Sílu, která působí na záporně nabitou desku, určíme ze vztahu

  \[F_-\,=\,QE_+\,,\]

  kde Q je velikost náboje záporně nabité desky a E₊ je velikost intenzity „od kladně nabité desky“.

  Podobně určíme sílu na kladně nabitou desku jako \[F_+\,=\,QE_-.\]

  Obě síly jsou stejně velké. Jejich velikost budeme dále označovat F_e.

  Oba vektory \(\vec{E}_+\) a \(\vec{E}_-\) jsou stejně velké a mezi deskami mají i stejný směr. Proto platí

  \[E_+\,=\,E_-\,=\,\frac{E}{2}\,,\]

  kde E je velikost celkové intenzity elektrického pole uvnitř kondenzátoru.

  Intenzita elektrického pole uvnitř kondenzátoru je dána vztahem:

  \[E\,=\,\frac{U_1}{d}.\]

  Intenzitu dosadíme do vzorce pro sílu:

  \[F_\mathrm{e} \,=\, Q\frac{E}{2}\,=\,Q\frac{U_1}{2d}.\]

  Náboj kondenzátoru získáme pomocí kapacity a napětí ze vztahu \(Q=C_1U_1\).

  \[ F_\mathrm{e}\,=\,\frac{C_1U_1^2}{2d}.\tag{*}\]

  Zbývá ještě vypočítat kapacitu deskového kondenzátoru, která závisí na ploše desek, permitivitě prostředí a vzdálenosti desek podle vzorce:

  \[C_1\,=\,\frac{\varepsilon S}{d}.\]

  Poznámka: Permitivita prostředí \(\varepsilon\) je skutečná permitivita daného prostředí mezi deskami kondenzátoru. Je tedy rovna součinu relativní permitivity prostředí \(\varepsilon_\mathrm{r}\) a permitivity vakua \(\varepsilon_0\).

  Kapacitu dosadíme do vzorce (*) a máme vyjádřenou sílu, kterou se desky kondenzátoru přitahují:

  \[F_\mathrm{e}\,=\,\frac{\varepsilon S U_1^2}{2d^2}.\]

• Nápověda: Vykonaná práce

  Práce, kterou musíme vykonat, abychom desky od sebe oddálili, závisí na síle, kterou musíme překonat, a na vzdálenosti, o kterou desky posuneme.

• Nápověda: Změna veličin při oddalování desek

  Jestliže je kondenzátor odpojený od zdroje, zůstává na něm stejný náboj. Pokud měníme vzdálenost desek, mění se jeho kapacita a tedy i napětí.

• I. Rozbor: Vykonaná práce

  Práce, kterou musíme vykonat při oddálení desek na dvojnásobnou vzdálenost, závisí na síle, kterou musíme překonávat, a vzdálenosti, o kterou desky posuneme.

  Po posunutí mají desky dvojnásobnou vzdálenost, posunuli jsme je tedy o vzdálenost d.

  Při oddalování desek překonáváme elektrickou sílu, kterou se desky přitahují (tu jsme si spočítali v předchozí části Síla působící na desky kondenzátoru). Protože při posouvání desek se nemění náboj na kondenzátoru, ale mění se napětí (kondenzátor je odpojený od zdroje), vyjádříme si tuto sílu pomocí náboje.

• I. Řešení: Vykonaná práce

  Při oddalování desek překonáváme elektrickou sílu F_e, kterou se desky přitahují. Spočítali jsme ji v předchozí části řešení Síla působící na desku kondenzátoru:

  \[F_\mathrm{e}\,=\,\frac{\varepsilon S U_1^2}{2d^2}.\]

  Napětí na kondenzátoru se při oddalování desek kondenzátoru mění, ale náboj zůstává stejný, protože je kondenzátor odpojený od zdroje. Proto si sílu působící na desku kondenzátoru vyjádříme pomocí veličin, které se při oddalování nemění, tj. náboj a plocha kondenzátoru:

  \[F_\mathrm{e}\,=\,\frac{\varepsilon S {\left( \frac{Q}{C_1}\right)}^2}{2d^2}\,=\,\frac{\varepsilon S }{2d^2} \,\frac{Q^2}{C_1^2}\,=\,\frac{\varepsilon S }{2d^2} \,\frac{Q^2d^2}{\varepsilon^2 S^2}\,=\,\frac{Q^2}{2\varepsilon S}.\]

  Vidíme, že síla během oddalování desek nezávisí na d. Vykonanou práci můžeme spočítat z následujícího vztahu:

  \[W\,=\,Fd\,,\]

  kde d je vzdálenost, o kterou jsme desky kondenzátoru posunuli.

  Pro vykonanou práci dostáváme po dosazení síly vztah:

  \[W\,=\,\frac{Q^2}{2\varepsilon S}d.\]

  Náboj si nyní můžeme opět vyjádřit pomocí počátečního napětí a kapacity \(Q=C_1U_1\):

  \[W\,=\,\frac{C_1^2 U_1^2d}{2\varepsilon S}\,=\,\frac{\varepsilon^2 S^2 U_1^2 d}{2\varepsilon S d^2}.\]

  Výraz zkrátíme a získáme práci potřebnou k oddálení desek na dvojnásobnou vzdálenost:

  \[W\,=\,\frac{\varepsilon S U_1^2}{2d}.\]

• II. Rozbor: Vykonaná práce počítaná přes energii

  Při oddalování desek kondenzátoru platí zákon zachování energie. Vykonaná práce je proto rovna rozdílu elektrické energie kondenzátoru po a před vzdálením desek.

  Elektrická energie kondenzátoru závisí na permitivitě, kvadrátu napětí, ploše kondenzátoru a vzdálenosti desek.

• II. Řešení: Vykonaná práce počítaná přes energii

  Na začátku byla energie kondenzátoru rovna:

  \[E_1\,=\,\frac{1}{2}\,C_1 U_1^2.\]

  Při oddalování desek se napětí na kondenzátoru mění, proto si ho vyjádříme pomocí náboje, který zůstává konstantní:

  \[U_1\,=\,\frac{Q}{C_1},\] \[E_1\,=\,\frac{1}{2}\,C_1 \frac{Q^2}{C_1^2}\,=\,\frac{1}{2}\, {\frac{Q^2}{C_1}}.\]

  Pro energii kondenzátoru tedy platí vztah:

  \[E_1\,=\,\frac{1}{2}\, {\frac{Q^2d}{\varepsilon S}}.\tag{1}\]

  Po oddálení desek se energie zvětšila, protože desky jsou nyní vzdáleny 2d:

  \[E_2\,=\,\frac{1}{2}\, {\frac{Q^2}{C_2}}\,=\,\frac{1}{2} \,{\frac{Q^2 2d}{\varepsilon S}}\,=\,\ {\frac{Q^2 d}{\varepsilon S}}.\tag{2}\]

  Platí zákon zachování energie. Vykonaná práce je tedy rovna rozdílu elektrických energií kondenzátoru:

  \[W\,=\,E_2-E_1.\]

  Dosadíme za energie E₁, E₂ vztahy (1) a (2):

  \[W\,=\,{\frac{Q^2 d}{\varepsilon S}} \,-\,\frac{1}{2} \,{\frac{Q^2d}{\varepsilon S}}\,=\,\frac{1}{2} \,{\frac{Q^2d}{\varepsilon S}}.\]

  Nyní můžeme opět náboj vyjádřit pomocí zadaného počátečního napětí a kapacity:

  \[W\,=\,\frac{1}{2} \,{\frac{ \left( C_1 U_1 \right)^2 d}{\varepsilon S}}\,=\,\frac{1}{2} \,{\frac{ \varepsilon^2 S^2 \, U_1^2 \, d}{d^2 \, \varepsilon S}}\,=\,{\frac{ \varepsilon S \, U_1^2}{2d}}.\]

• Odpověď

  Na desky kondenzátoru působí síla

  \[F_\mathrm{e}=\frac{\varepsilon S U_1^2}{2d^2}\,\,.\]

  Pokud desky oddálíme na dvojnásobnou vzdálenost, vykonáme práci

  \[W=\frac{\varepsilon S U_1^2}{2d}\,\,.\]