Sbírka řešených úloh

Čtyři náboje

Úloha číslo: 271

• Obrázek a označení

  

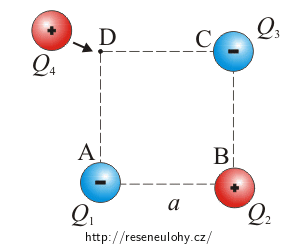
  Jednotlivé náboje očíslujeme a vrcholy čtverce po řadě označíme písmeny. Úlohu budeme počítat obecně a až na konci dosadíme stejnou velikost nábojů a jejich znaménka.

• Nápověda: Vykonaná práce

  Práce vykonaná elektrickou silou při přenesení náboje v elektrickém poli závisí pouze na velikosti přeneseného náboje a rozdílu potenciálu v počátečním a koncovém bodě.

  Při výpočtu práce potřebné na shromáždění všech nábojů, musíme vyjádřit práci, kterou je třeba vykonat na přinesení každého náboje zvlášť do daného vrcholu při vytváření celé konfigurace nábojů a tyto příspěvky pak sečíst.

• Nápověda: Potenciál

  Celkový potenciál elektrického pole v jednom vrcholu čtverce získáme součtem potenciálů elektrických polí, které vytváří náboje v ostatních vrcholech čtverce.

  Pro potenciál bodového náboje platí:

  $$\varphi\,=\, \frac{1}{4 \pi \varepsilon_0} \,\frac{Q}{r}\,.$$

• Rozbor

  Při přenášení náboje v elektrickém poli koná elektrická síla práci, která je rovna rozdílu elektrické potenciální energie v počátečním a koncovém bodě. Do posledního rohu čtverce přenášíme náboj z nekonečna, kde zvolíme elektrickou potenciální energii rovnu nule. Potřebná práce je tedy až na znaménko rovna potenciální energii v koncovém bodě.

  Elektrická potenciální energie v daném bodě je přímo úměrná náboji (včetně znaménka) a potenciálu elektrického pole v tomto bodě.

  Abychom spočetli celkový potenciál elektrického pole, musíme sečíst potenciály elektrických polí, které vytváří jednotlivé náboje. Potenciál elektrického pole v posledním vrcholu čtverce je tedy dán součtem potenciálů elektrických polí, které vytváří náboje ve třech ostatních vrcholech čtverce.

  Potenciál elektrického pole jednoho bodového náboje je přímo úměrný velikosti náboje a nepřímo úměrný jeho vzdálenosti od místa, kde potenciál zjišťujeme.

  Abychom vypočítali práci na shromáždění všech nábojů, musíme vyjádřit práce potřebné na přenesení každého jednotlivého náboje. Na pořadí, v jakém budeme náboje přenášet do čtverce, nezáleží. Při výpočtu jednotlivých prací musíme dát pozor, jaké náboje „jsme již shromáždili“ a které tedy vytváří pole ve vrcholu, kam přesouváme další náboj.

• Řešení: Práce na přidání posledního náboje Q

  Práce vykonaná elektrickou silou při přenesení náboje v elektrickém poli je rovna rozdílu potenciální energie v počátečním bodě 1 a koncovém bodě 2:

  $$W_\mathrm{e}\,=\, E_\mathrm{p1} - E_\mathrm{p2}.$$

  Přenášíme-li náboj z nekonečna, kde volíme potenciální energii rovnou nule (E_p1 = 0), pak je práce rovna záporně vzaté potenciální energii v koncovém bodě 2:

  $$W_\mathrm{e}\,=\,-E_\mathrm{p2}.$$

  V našem případě přenášíme náboj z nekonečna do vrcholu čtverce D. Práce je tedy rovna:

  $$W_\mathrm{e}\,=\, -E_\mathrm{pD}.$$

  Pokud znaménko mínus vynecháme, vyjádříme práci, kterou vykonala vnější síla přemísťující náboj (viz komentář na konci úlohy):

  $$W\,=\, E_\mathrm{pD}.$$

  Potenciální energii vyjádříme pomocí potenciálu a náboje: $$E_\mathrm{pD}\,=\,Q_4 \varphi_\mathrm{D}$$ a dosadíme do vztahu pro výpočet práce:

  $$W\,=\,Q_4 \varphi_\mathrm{D}\,.\tag{*}$$

  Nyní spočítáme potenciál elektrického pole v bodě D. Elektrické pole vytváří náboje umístěné v ostatních třech vrcholech čtverce. Potenciál celkového elektrického pole v bodě D je roven součtu potenciálů elektrických polí jednotlivých nábojů:

  $$\varphi_\mathrm{D}\,=\,\varphi_\mathrm{1D} + \varphi_\mathrm{2D} + \varphi_\mathrm{3D}\,,\tag{**}$$

  kde φ_1D je potenciál pole prvního náboje, φ_2D potenciál pole druhého náboje a φ_3D potenciál pole třetího náboje v bodě D.

  Pro potenciál elektrického pole náboje Q ve vzdálenosti r od náboje platí obecný vztah:

  $$\varphi\,=\,\frac{1}{4 \pi \epsilon_0}\frac{Q}{r}\,.$$

  První a třetí náboj mají od bodu D vzdálenost a. Druhý náboj je od bodu D vzdálen a√2 (a√2 je délka úhlopříčky ve čtverci o straně a). Pro potenciály tedy platí:

  $\varphi_\mathrm{1D}\,=\,\frac{1}{4 \pi \epsilon_0}\,\frac{Q_1}{a}\,, \hspace{30px} \varphi_\mathrm{2D}\,=\,\frac{1}{4 \pi \epsilon_0}\,\frac{Q_2}{a \sqrt{2}}\,, \hspace{30px} \varphi_\mathrm{3D}\,=\,\frac{1}{4 \pi \epsilon_0}\,\frac{Q_3}{a}$.

  Vyjádření jednotlivých potenciálů dosadíme do vzorce (**):

  $$\varphi_\mathrm{D}\,=\,\frac{1}{4 \pi \epsilon_0}\,\frac{Q_1}{a} \,+\, \frac{1}{4 \pi \epsilon_0}\,\frac{Q_2}{a \sqrt{2}}\, +\, \frac{1}{4 \pi \epsilon_0}\,\frac{Q_3}{a}.$$

  Vytkneme konstantu $\frac{1}{4 \pi \varepsilon_0}$:

  $$\varphi_\mathrm{D}\,=\,\frac{1}{4 \pi \epsilon_0}\, \left(\frac{Q_1}{a} \,+\, \frac{Q_2}{a \sqrt{2}}\, +\, \frac{Q_3}{a}\right).$$

  Vyjádřený potenciál dosadíme do vzorce pro výpočet práce (**):

  $$W\,=\, \frac{Q_4}{4 \pi \epsilon_0}\, \left(\frac{Q_1}{a} \,+\, \frac{Q_2}{a \sqrt{2}}\, +\, \frac{Q_3}{a}\right).$$

  Získali jsme obecný vztah pro výpočet práce na přemístění náboje Q₄ do vrcholu D. Nyní ještě dosadíme stejnou velikost nábojů a jejich znaménka Q₁ = Q₃ = − Q a Q₂ = Q₄ = Q:

  $$W\,=\, \frac{Q}{4 \pi \epsilon_0}\, \left(\frac{-Q}{a} \,+\, \frac{Q}{a \sqrt{2}}\, +\, \frac{-Q}{a}\right).$$

  Vytkneme $\frac{Q}{a}$ a upravíme výraz v závorce:

  $$W\,=\, \frac{Q^2}{4 \pi \epsilon_0 a}\, \left(-1 \,+\, \frac{1}{\sqrt{2}}\, -1\right)\,=\, \frac{Q^2}{4 \pi \epsilon_0 a}\, \left(-2 \,+\, \frac{1}{\sqrt{2}}\right).$$

  Vyjádřili jsme práci, kterou vykoná vnější síla při přenesení náboje Q z nekonečna do rohu čtverce.

  Jelikož vyšla práce vnější síly záporná, konala ve skutečnosti práci síla elektrická.

• Řešení: Práce na shromáždění všech nábojů

  Abychom vypočítali celkovou práci na shromáždění všech nábojů, vyjádříme si nejdříve práce, které musí vnější síla vykonat na přidání jednotlivých nábojů postupně do vrcholů čtverce. Z vlastností elektrostatického pole plyne, že na pořadí, v jakém budeme jednotlivé náboje přinášet, nezáleží.

  K výpočtu jednotlivých prací využijeme stejného vzorce (*) jako v předchozí části řešení:

  $$W\,=\, Q \varphi\,,$$

  kde Q je velikost přidávaného náboje včetně znaménka a φ je potenciál elektrického pole ve vrcholu čtverce, do kterého náboj přidáváme.

  Potenciál elektrického pole vytvořeného jednotlivými náboji vyjádříme ze vztahu:

  $$\varphi\,=\, \frac{1}{4 \pi \varepsilon_0}\, \frac{Q}{r}\,,$$

  kde r je vzdálenost náboje od místa, kde potenciál zjišťujeme.

  Práce na přenesení náboje Q₁ do vrcholu A:

  Při umístění prvního náboje nemusíme vykonat žádnou práci, protože nemusíme překonávat žádnou elektrickou sílu (zatím zde není žádné elektrické pole):

  $$W_1\,=\,0.$$

  Práce na přenesení náboje Q₂ do vrcholu B:

  Nyní už musíme překonávat sílu elektrického pole, které vytváří v bodě B náboj Q₁. Práci vyjádříme ze vzorce:

  $$W_2\,=\, Q_2 \varphi_\mathrm{B}\,,$$

  kde φ_1B je potenciál elektrického pole vytvořeného nábojem Q₁ v bodě B.

  Náboj Q₁ je ve vzdálenosti a od vrcholu. Potenciál ve vrcholu B je tedy roven:

  $$\varphi_\mathrm{B}\,=\, \frac{1}{4 \pi \varepsilon_0}\, \frac{Q_1}{a}\,.$$

  Potenciál dosadíme do vzorce pro práci:

  $$W_2\,=\, \frac{1}{4 \pi \varepsilon_0}\, \frac{Q_1 Q_2}{a}.$$

  Dosadíme velikosti a znaménka nábojů Q₁ = −Q a Q₂ = Q:

  $$W_2\,=\, - \frac{1}{4 \pi \varepsilon_0}\, \frac{ Q^2}{a}.$$

  Práce vnější síly vyšla záporná, protože kladný náboj je přitahován z „nekonečna“ záporným nábojem umístěným ve vrcholu čtverce. Práci na přenesení druhého náboje tedy vykonala elektrická síla.

  Práce na přenesení náboje Q₃ do vrcholu C:

  Práci vypočítáme opět ze vztahu:

  $$W_3\,=\, Q_3 \varphi_\mathrm{C}\,.$$

  Elektrické pole v bodě C vytváří náboj Q₁ ve vzdálenosti a√2 a náboj Q₂ ve vzdálenosti a.

  Potenciál je tedy roven:

  $$\varphi_\mathrm{C}\,=\,\varphi_\mathrm{1C} \,+\,\varphi_\mathrm{2C}\,=\,\frac{1}{4 \pi \varepsilon_0}\, \frac{Q_1}{a \sqrt{2}}\,+\,\frac{1}{4 \pi \varepsilon_0}\, \frac{Q_2}{a}\,,$$ $$\varphi_\mathrm{C}\,=\,\frac{1}{4 \pi \varepsilon_0}\, \left(\frac{Q_1}{a \sqrt{2}}\,+\frac{Q_2}{a}\right)\,.$$

  Práce je pak rovna:

  $$W_3\,=\, \frac{Q_3}{4 \pi \varepsilon_0}\, \left(\frac{Q_1}{a \sqrt{2}}\,+\frac{Q_2}{a}\right)\,.$$

  Dosadíme velikosti a znaménka nábojů Q₁ = Q₃ = − Q a Q₂ = Q:

  $$W_3\,=\, \frac{-Q}{4 \pi \varepsilon_0}\, \left( \frac{-Q}{a \sqrt{2}}\,+\frac{Q}{a}\right)\,=\,- \frac{1}{4 \pi \varepsilon_0 }\,\frac{Q^2}{a} \, \left( 1-\frac{1}{ \sqrt{2}}\right).$$

  Práce na přenesení náboje Q₄ do vrcholu D:

  Práci na přenesení posledního náboje jsme vypočítali v předchozí části řešení:

  $$W_4\,=\, \frac{Q^2}{4 \pi \epsilon_0 a}\, \left(-2 \,+\, \frac{1}{\sqrt{2}}\right).$$

  Celkovou práci, kterou musíme vykonat, abychom shromáždili všechny náboje, získáme součtem jednotlivých prací.

  $$W\,=\,W_1+W_2+W_3+W_4,$$ $$W\,=\,0\,+\,\frac{1}{4 \pi \varepsilon_0}\, \frac{- Q^2}{a}+ \frac{1}{4 \pi \varepsilon_0 }\,\frac{Q^2}{a} \, \left(\frac{1}{ \sqrt{2}}\,-1\right)+\frac{Q^2}{4 \pi \epsilon_0 a}\, \left(-2 \,+\, \frac{1}{\sqrt{2}}\right).$$

  Vytkneme $\frac{1}{4 \pi \varepsilon_0}\, \frac{ Q^2}{a}$ a sečteme čísla v závorce:

  $$W\,=\,\frac{1}{4 \pi \varepsilon_0}\, \frac{Q^2}{a}\left(-1 + \frac{1}{ \sqrt{2}}\,-1 -2 \,+\, \frac{1}{\sqrt{2}}\right)\,=\,\frac{1}{4 \pi \varepsilon_0}\, \frac{Q^2}{a}\left(-4 \,+\, \frac{2}{\sqrt{2}}\right),$$ $$W\,=\,\frac{1}{4 \pi \varepsilon_0}\, \frac{Q^2}{a}\left(-4 \,+\,\sqrt{2}\right).$$

  Jelikož vyšla práce vnější síly záporná, konala ve skutečnosti práci síla elektrická.

• Odpověď

  Na přidání posledního náboje do vrcholu čtverce musí vnější síla vykonat práci

  $$W\,=\, \frac{Q^2}{4 \pi \epsilon_0 a}\, \left(-2 \,+\, \frac{1}{\sqrt{2}}\right)\,.$$

  Na shromáždění všech nábojů musí vnější síla vykonat práci

  $$W\,=\,\frac{1}{4 \pi \varepsilon_0}\, \frac{Q^2}{a}\left(-4 \,+\, \frac{2}{\sqrt{2}}\right)\,.$$

  Jelikož v obou případech vyšla práce vnější síly záporná, konala ve skutečnosti práci síla elektrická.

• Komentář: Znaménko práce

  Pokud se má náboj přesunout z místa s vyšší elektrickou potenciální energií do místa s nižší elektrickou potenciální energií, koná práci elektrická síla, tj. těleso se bude tímto směrem pohybovat vlivem elektrické síly. Elektrická potenciální energie v tomto případě klesá a dochází ke zvyšování např. kinetické energie elektronu (elektron je urychlován).

  V opačném případě koná práci vnější síla, zvyšuje tím elektrickou potenciální energii elektronu. V tomto případě se těleso bude tímto směrem pohybovat pod vlivem vnější síly, která překonává elektrickou sílu.

  Je to stejné jako v tíhovém poli. Padá-li těleso dolů, tak se vlastně pohybuje z místa s vyšší tíhovou potenciální energií do místa s nižší tíhovou potenciální energií, a práci koná tíhová síla. Pokud těleso zvedáme do výšky, koná práci vnější síla.

  Vyjde-li práce dané síly záporná, znamená to, že situace je ve skutečnosti opačná, než jak jsme předpokládali. Práci tedy koná síla opačného směru.

• Výpočet práce přímou integrací

  Práci, kterou vykoná elektrická síla, při přenesení náboje z místa a do místa b vypočítáme ze vztahu: $$W_\mathrm{e}\,=\, \int_\mathrm{a}^\mathrm{b} \vec{F}_\mathrm{v} \cdot \mathrm{d}\vec{r}\,,$$

  kde F_v je výsledná elektrická síla, která působí na přenášený náboj.

  Vzhledem k tomu, že práce elektrických sil nezávisí na trajektorii, zvolíme si jako trajektorii, po které se bude náboj pohybovat, polopřímku, která míří do středu čtverce (viz obrázek). Označíme si polohový vektor $\vec{r}$ (počátek bude mít ve středu čtverce) a vyjádříme výslednou elektrickou sílu $\vec{F}_\mathrm{v}$ v obecném místě na zvolené trajektorii.

  Do obrázku zakreslíme elektrické síly, které působí na náboj Q₄.

  

  

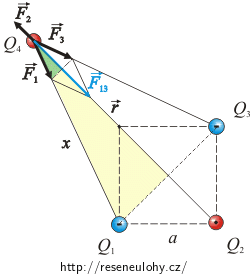  $$\vec{F}_\mathrm{v}\,=\,\vec{F}_1\,+\,\vec{F}_2\,+\,\vec{F}_3\,=\,\vec{F}_{13}\,+\,\vec{F}_2$$ $$F_\mathrm{v}\,=\,F_{13}\,-\,F_2$$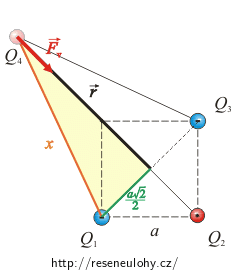

  Nejdříve vyjádříme velikost síly F₂ z Coulombova zákona:

  $$F_2\,=\,k\,\frac{Q_2 Q_4}{\left( r+ \frac{a \sqrt{2}}{2}\right)^2}\,=\,k\,\frac{Q^2}{\left( r+ \frac{a \sqrt{2}}{2}\right)^2}.$$

  Vyjádření velikosti síly F₁₃, což je výslednice sil F₁ a F₃, bude mít více kroků.

  1. Vyjádříme síly F₁ a F₃ opět z Coulombova zákona.
  2. Výslednici F₁₃ vypočítáme z podobnosti zeleného a žlutého trojúhelníku.
  3. Vyjádříme vzdálenost x pomocí r.

  1) Protože náboje Q₁ a Q₃ jsou od náboje Q₄ ve stejné vzdálenosti a všechny náboje mají stejnou velikost, bude i velikost síly F₁ a F₃ stejná:

  $$F_1\,=\,F_3\,=\,k\, \frac{Q^2}{x^2}.\tag{1}$$

  2) Z podobnosti zeleného a žlutého trojúhelníka platí:

  $$\frac{\frac{F_{13}}{2}}{F_1}\,=\,\frac{r}{x},$$ $$F_{13}\,=\,\frac{2 F_1 r}{x}.$$

  Dosadíme velikost síly F₁ ze vzorce (1):

  $$F_{13}\,=\,\frac{2 k\, \frac{Q^2}{x^2} r}{x}\,=\,\frac{2 k Q^2 r}{x^3}.\tag{2}$$

  3) Zbývá vyjádřit ze žlutého trojúhelníka vzdálenost x pomocí r. Použijeme Pythagorovu větu.

  $$x\,=\,\sqrt{\left(\frac{a \sqrt{2}}{2}\right)^2 +r^2}\,=\,\sqrt{\frac{2a^2}{4} +r^2},$$ $$x\,=\,\sqrt{\frac{a^2}{2} +r^2}.$$

  X dosadíme do vzorce (2):

  $$F_{13}\,=\,\frac{2 k Q^2 r}{\sqrt{\left(\frac{a^2}{2} +r^2\right)^3}}.$$

  Výslednou sílu tedy vypočítáme:

  $$F_\mathrm{v}\,=\,F_{13}\,-\,F_2\,=\,\frac{2 k Q^2 r}{\sqrt{\left(\frac{a^2}{2} +r^2\right)^3}}\,-\, k\,\frac{Q^2}{\left( r+ \frac{a \sqrt{2}}{2}\right)^2} \,.$$

  Vyjádřili jsme tedy výslednici elektrické síly, zbývá už „jen“ vypočítat integrál vyjadřující práci. Protože vektor síly $\vec{F}_\mathrm{v}$ je rovnoběžný s vektorem $\vec{r}$, můžeme skalární součin v integrálu zjednodušit:

  $$W_\mathrm{e}\,=\, \int_\mathrm{a}^\mathrm{b} \vec{F}_\mathrm{v} \cdot \mathrm{d}\vec{r}\,=\,-\int_\mathrm{a}^\mathrm{b} F_\mathrm{v} \mathrm{d}r.$$

  Mínus je před integrálem proto, že vektory $\vec{r}$ a $\vec{F}_\mathrm{v}$ jsou opačně orientované.

  Určíme integrační meze. Náboj přenášíme z nekonečna až do rohu čtverce, kde je r rovno polovině úhlopříčky čtverce $r\,=\, \frac{a \sqrt{2}}{2}$:

  $$W_\mathrm{e}\,=\, -\int_\infty^{\frac{a \sqrt{2}}{{2}}} F_\mathrm{v} \mathrm{d}r.$$

  Dosadíme vyjádření elektrické síly:

  $$W_\mathrm{e}\,=\, -\int_\infty^{\frac{a \sqrt{2}}{{2}}} \left( \frac{2 k Q^2 r}{\sqrt{\left(\frac{a^2}{2} +r^2\right)^3}}\,-\, k\,\frac{Q^2}{\left( r+ \frac{a \sqrt{2}}{2}\right)^2} \right) \mathrm{d}r.$$

  Integrál vypočítáme v následujícím oddíle. Výsledek, který získáme, odpovídá řešení pomocí potenciální energie, tj.

  $$W_\mathrm{e}\,=\,-\, \frac{k Q^2}{a} \left( -2 + \,\frac{1}{\sqrt{2}}\right)\,.$$

• Výpočet integrálu

  V tomto oddíle vypočítáme integrál:

  $$W_\mathrm{e}\,=\, -\int_\infty^{\frac{a \sqrt{2}}{{2}}} \left( \frac{2 k Q^2 r}{\sqrt{\left(\frac{a^2}{2} +r^2\right)^3}}\,-\, k\,\frac{Q^2}{\left( r+ \frac{a \sqrt{2}}{2}\right)^2} \right) \mathrm{d}r\,.$$

  Integrál rozdílu je roven rozdílu integrálů. Pozor na znaménko mínus před celým integrálem:

  $$W_\mathrm{e}\,=\,-\int_\infty^{\frac{a \sqrt{2}}{{2}}} \frac{2 k Q^2 r}{\sqrt{\left(\frac{a^2}{2} +r^2\right)^3}}\,\mathrm{d}r \,+\, \int_\infty^{\frac{a \sqrt{2}}{{2}}}\, k\,\frac{Q^2}{\left( r+ \frac{a \sqrt{2}}{2}\right)^2} \mathrm{d}r.$$

  Nejdříve budeme počítat první integrál, který si označíme jako I₁:

  $$I_1\,=\,-\int_\infty^{\frac{a \sqrt{2}}{{2}}} \frac{2 k Q^2 r}{\sqrt{\left(\frac{a^2}{2} +r^2\right)^3}}\,\mathrm{d}r.$$

  Vyjmeme konstanty před integrál:

  $$I_1\,=\,-k Q^2\int_\infty^{\frac{a \sqrt{2}}{{2}}} \frac{2 r}{\sqrt{\left(\frac{a^2}{2} +r^2\right)^3}}\,\mathrm{d}r.$$

  K výpočtu integrálu použijeme substituci. (Meze nebudeme přepočítávat, ale později dosadíme zpět za t a použijeme meze původní.) Integrál vypočítáme:

  $$t\,=\,\frac{a^2}{2} +r^2,$$ $$\mathrm{d}t\,=\,2r\,\mathrm{d}r,$$ $$I_1\,=\,-k Q^2\int \frac{\mathrm{d}t}{t^{\frac{3}{2}}}\, =\,-k Q^2 \,\left[-\,\frac{2}{t^{\frac{1}{2}}}\right]\,.$$

  Dosadíme zpět za t:

  $$I_1\,=\,-k Q^2 \,\left[-\,\frac{2}{\left(\frac{a^2}{2} +r^2\right)^{\frac{1}{2}}}\right]_\infty^{\frac{a \sqrt{2}}{{2}}}\,$$ $$I_1\,=\,k Q^2 \,\frac{2}{\sqrt{\frac{a^2}{2} +\left(\frac{a \sqrt{2}}{{2}}\right)^2}}\,=\,k Q^2 \,\frac{2}{\sqrt{\frac{a^2}{2} +\frac{2a^2 }{4}}}\,=\,k Q^2 \,\frac{2}{\sqrt{\frac{a^2}{2} +\frac{a^2 }{2}}}$$ $$I_1\,=\, \,\frac{2k Q^2}{a}.$$

   

  Nyní vypočítáme druhý integrál, který si označíme I₂:

  $$I_2\,=\,\int_\infty^{\frac{a \sqrt{2}}{{2}}}\, k\,\frac{Q^2}{\left( r+ \frac{a \sqrt{2}}{2}\right)^2} \mathrm{d}r.$$

  Konstanty vyjmeme před integrál:

  $$I_2\,=\,kQ^2\,\int_\infty^{\frac{a \sqrt{2}}{{2}}}\, \,\frac{\mathrm{d}r}{\left( r+ \frac{a \sqrt{2}}{2}\right)^2} .$$

  K výpočtu opět použijeme substituci:

  $$t\,=\,r\,+\,\frac{a \sqrt{2}}{2},$$ $$\mathrm{d}t\,=\,\mathrm{d}r,$$ $$I_2\,=\,kQ^2\,\int \frac{\mathrm{d}t}{t^2}\,=\,kQ^2\,\left[-\,\frac{1}{t}\right] .$$

  Dosadíme zpět za t:

  $$I_2\,=\,kQ^2\,\left[-\,\frac{1}{r\,+\,\frac{a \sqrt{2}}{2}}\right]_\infty^{\frac{a \sqrt{2}}{{2}}} ,$$ $$I_2\,=\,-\,kQ^2\,\frac{1}{\frac{a \sqrt{2}}{{2}}\,+\,\frac{a \sqrt{2}}{2}}\,=\,-\,kQ^2\,\frac{1}{a \sqrt{2}},$$ $$I_2\,=\,-\,\frac{kQ^2}{a \sqrt{2}}.$$

  Vypočítali jsme tedy celý integrál:

  $$W_\mathrm{e}\,=\,I_1 + I_2\,=\,-\,\frac{2k Q^2}{a} +\,\frac{kQ^2}{a \sqrt{2}},$$ $$W_\mathrm{e}\,=\,\,\frac{k Q^2}{a}\left(-2+\,\frac{1}{ \sqrt{2}}\right).$$

• Jiný způsob výpočtu práce na seskupení nábojů

  Práci, kterou vykoná vnější síla na shromáždění všech nábojů, můžeme spočítat také pomocí potenciální energie celé soustavy.

  $$W\,=\,E_\mathrm{p}.$$

  Stačí tedy vyjádřit potenciální energii soustavy.

  Dvojice nábojů Q₁ a Q₂, které jsou od sebe vzdáleny r, má potenciální energii:

  $$E_\mathrm{p12}\,=\, \frac{1}{4 \pi \varepsilon_0} \, \frac{Q_1 Q_2}{r}\,.$$

  Pokud máme více nábojů, získáme potenciální energii celé soustavy součtem potenciálních energií všech dvojic nábojů. V našem případě máme 4 náboje, ze kterých můžeme vytvořit 6 různých dvojic:

  $$E_\mathrm{p}\,=\, E_\mathrm{p12}\,+\,E_\mathrm{p13}\,+\,E_\mathrm{p14}\,+\,E_\mathrm{p23}\,+\,E_\mathrm{p24}\,+\,E_\mathrm{p34}.$$

  Dosadíme potenciální energii jednotlivých dvojic a rovnou vytkneme konstantu $\frac{1}{4 \pi \varepsilon_0}$:

  $$E_\mathrm{p}\,=\, \frac{1}{4 \pi \varepsilon_0} \left(\, \frac{Q_1 Q_2}{a} \,+ \, \frac{Q_1 Q_3}{a\sqrt{2}}\,+\, \frac{Q_1 Q_4}{a}\,+\, \frac{Q_2 Q_3}{a}\,+ \, \frac{Q_2 Q_4}{a\sqrt{2}}\,+\, \frac{Q_3 Q_4}{a} \right).$$

  Doplníme velikosti a znaménka nábojů Q₁ = Q₃ = − Q, Q₂ = Q₄ = Q:

  $$E_\mathrm{p}\,=\, \frac{1}{4 \pi \varepsilon_0} \,\left( -\, \frac{Q^2}{a}\, +\, \frac{Q^2}{a\sqrt{2}}\, -\, \frac{Q^2}{a}\, -\, \frac{Q^2}{a}\, +\, \frac{Q^2}{a\sqrt{2}}\, -\, \frac{Q^2}{a} \right).$$

  Postupně upravíme výraz v závorce:

  $$E_\mathrm{p}\,=\, \frac{1}{4 \pi \varepsilon_0} \,\frac{Q^2}{a}\left( -\, 1\, +\, \frac{1}{\sqrt{2}}\, -\, 1\, -\, 1\, +\, \frac{1}{\sqrt{2}}\, -\, 1 \right),$$ $$E_\mathrm{p}\,=\, \frac{1}{4 \pi \varepsilon_0} \,\frac{Q^2}{a}\left(-4\,+\, \frac{2}{\sqrt{2}} \right).$$

  Práce vnější síly je tedy rovna

  $$W\,=\, \frac{1}{4 \pi \varepsilon_0} \,\frac{Q^2}{a}\left(-4\,+\, \frac{2}{\sqrt{2}} \right)\,,$$

  což odpovídá výsledku získanému sčítáním práce při postupném přidávání jednotlivých nábojů.