Sbírka řešených úloh

Letící elektron v homogenním poli

Úloha číslo: 31

• I. Nápověda 1

  Jak velká síla na elektron působí a jaký má směr?

  Rozmyslete si, o jaký pohyb se jedná.

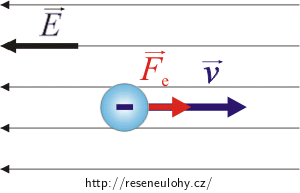
• Obrázek

  

• I. Nápověda 2

  Zrychlení elektronu můžeme spočítat z 2. Newtonova zákona.

• I. Rozbor

  Na pohybující se elektron bude působit elektrická síla úměrná intenzitě homogenního pole. Protože elektron má záporný náboj, bude mít síla opačný směr než vektor elektrické intenzity. To znamená, že síla bude působit ve směru pohybu elektronu a elektron bude touto silou urychlován.

  K výpočtu rychlosti elektronu použijeme vztah pro dráhu rovnoměrně zrychleného pohybu, kde nesmíme zapomenout na počáteční rychlost elektronu. Zrychlení vyjádříme pomocí 2. Newtonova zákona a dobu pohybu si spočítáme pomocí vztahu pro rychlost rovnoměrně zrychleného pohybu.

• I. Řešení: Pohyb elektronu

  Na elektron bude působit elektrická síla o velikosti

  \[F_\mathrm{e}\,=\,eE\,.\tag{1}\]

  Protože náboj elektronu je záporný, bude mít síla opačný směr než elektrická intenzita \(\vec{E}\). Síla tedy bude mířit ve směru pohybu a elektron bude rovnoměrně zrychlovat. Pomocí 2. Newtonova zákona vyjádříme zrychlení a:

  \[a\,=\,\frac{F_\mathrm{e}}{m}.\]

  Za elektrickou sílu můžeme dosadit ze vzorce (1):

  \[a\,=\,\frac{eE}{m}\,.\tag{2}\]

  Elektron se pohybuje rovnoměrně zrychleně, pro jeho rychlost platí vztah

  \[v\,=\,at+v_0,\]

  přičemž jako v₀ jsme si označili počáteční rychlost elektronu.

  Z této rovnice si vyjádříme neznámý čas t:

  \[t\,=\,\frac{v-v_0}{a}.\tag{3}\]

  Pro dráhu rovnoměrně zrychleného pohybu platí vztah:

  \[s\,=\,\frac{1}{2}at^2+v_0t.\]

  Nyní můžeme dosadit za čas t ze vzorce (3):

  \[s\,=\,\frac{1}{2}a\left( \frac{v-v_0}{a}\right)^2+v_0\frac{v-v_0}{a}.\]

  Vztah budeme upravovat tak, abychom vyjádřili hledanou rychlost v:

  \[s\,=\,\frac{1}{2} \frac{\left( v-v_0\right)^2}{a}+\frac{v_0\left(v-v_0\right)}{a} \hspace{20px}|\,\cdot 2a,\] \[2sa\,=\,\left( v-v_0\right)^2 + 2v_0\left( v-v_0\right).\]

  Roznásobíme a zjistíme, že se nám některé členy odečtou:

  \[2sa\,=\,v^2 - 2v_0v + v_0^2 + 2v_0v - 2v_0^2,\] \[2sa\,=\,v^2 - v_0^2\hspace{20px}|\, +v_0^2,\] \[ v^2\,=\,2sa+v_0^2,\] \[v\,=\, \sqrt {2sa+v_0^2}.\]

  Do tohoto vzorce dosadíme za zrychlení a vztah (2) a získáme hledanou konečnou rychlost elektronu:

  \[v\,=\,\sqrt {\frac{2seE}{m}+v_0^2}.\]

• II. Nápověda

  Zauvažujte nad tím, jak a proč se při pohybu v homogenním poli mění energie elektronu.

• II. Rozbor

  K výpočtu rychlosti využijeme zákon zachování energie.

  Na letící elektron působí ve směru pohybu elektrická síla, která koná práci a tím zvětšuje kinetickou energii elektronu.

  Poznámka: Práce vykonaná elektrickou silou odpovídá změně elektrické potenciální energie.

• II. Řešení: Energie elektronu

  Pro letící elektron platí zákon zachování energie:

  \[E_\mathrm{k2}\,=\,E_\mathrm{k1}+W_\mathrm{e}.\tag{*}\]

  Kinetické energie elektronu zjistíme ze vztahů \[E_\mathrm{k1}\,=\,\frac{1}{2}m v_0^2\,,\hspace{40px} E_\mathrm{k2}\,=\,\frac{1}{2}m v^2\,,\] kde v₀ je počáteční rychlost elektronu.

  W_e je práce, kterou musela vykonat elektrická síla, aby elektron urychlila. Protože je elektrická síla konstantní, můžeme ji vypočítat ze vztahu:

  \[W_\mathrm{e}\,=\,F_\mathrm{e} s.\]

  Elektrická síla je přímo úměrná náboji elektronu e a intenzitě pole E: \(F_\mathrm{e}\,=\,eE\), tím dostáváme pro elektrickou práci vztah:

  \[W_\mathrm{e}\,=\,e E s.\]

  Vztahy pro jednotlivé členy dosadíme do zákona zachování energie (*) a vyjádříme neznámou rychlost v:

  \[\frac{1}{2}m v^2\,=\,\frac{1}{2}m v_0^2 + e E s \hspace{20px}| \,\cdot \frac{2}{m},\] \[v^2\,=\,v_0^2 + \frac{2seE}{m},\] \[v\,=\,\sqrt {\frac{2seE}{m}+v_0^2}.\]

• Zápis a číselný výpočet

  \[ \begin{eqnarray} v_0\,&=&\,10\,\mathrm{km\,s}=10^4\,\mathrm{m\,s^{-1}}\\ E\,&=&\,20\,\mathrm{V\,m^{-1}}\\ s\,&=&\,9\,\mathrm{cm}\,=\,9{\cdot} 10^{-2}\,\mathrm{m}\\ v\,&=&\,?\,\left(\mathrm{m\,s^{-1}}\right)\end{eqnarray}\]

  Z tabulek:

  \[e\,=\,1{,}6 {\cdot} 10^{-19}\,\mathrm{C}\] \[m\,=\,9{,}1 {\cdot} 10^{-31}\,\mathrm{kg}\]

  ---

  \[ \begin{eqnarray}v\,&=&\,\sqrt {\frac{2seE}{m}+v_0^2}\\ v\,&=&\,\sqrt {\frac{2\,\cdot\, 9{\cdot} 10^{-2} \,\cdot\, 1{,}6 {\cdot} 10^{-19}\,\cdot\, 20}{9{,}1 {\cdot} 10^{-31}}\,+\,\left(10^4\right)^2}\,\mathrm{m\,s^{-1}}\\ v \,&\dot=&\, 800\,\mathrm{km\,s^{-1}} \end{eqnarray}\]

  Všimněte si, že i když není elektrické pole moc silné, získá elektron i na malé dráze velkou rychlost. Je to způsobeno tím, že elektron je velmi lehký, a proto k jeho urychlení stačí malé množství energie.

• Odpověď

  Po uražení dráhy 9 cm bude mít elektron rychlost \(v\,=\,\sqrt {\frac{2seE}{m}+v_0^2}\,\,\dot=\,\,800\,\mathrm{km\,s^{-1}}\).

• Co by se změnilo, kdyby....

  Co by se změnilo, kdyby elektron vletěl do stejného homogenního pole ve směru siločar?

  

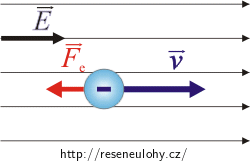
  V takovém případě by elektrická síla měla opačný směr než rychlost. Elektron by se pohyboval rovnoměrně zpomaleným pohybem.