Sbírka řešených úloh

Řešení obvodu metodou uzlových napětí

Úloha číslo: 1955

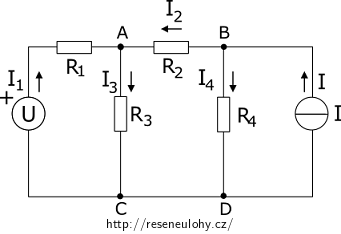
Řešte tento obvod pomocí metody uzlových napětí a spočtěte všechny neznámé proudy a napětí, jestliže víte : U = 100 V, R₁ = 100 Ω, R₂ = 200 Ω, R₃ = 300 Ω, R₄ = 400 Ω a I = 15 A.

• Připomenutí Kirchhoffových zákonů.

  Metoda smyčkových proudů vychází z Kirchhoffových zákonů, proto si je připomeňme.

  Základní pojmy:

  • Uzel je místo, ve kterém se stýká dva a více vodičů.
  • Větev obvodu je část obvodu mezi dvěma uzly tvořená jedním prvkem nebo několika prvky spojenými za sebou.
  • Smyčka je uzavřené dráha v části obvodu tvořená větvemi.

  První Kirchhoffův zákon

  Je to vlastně zákon zachování elektrického náboje. Stejnosměrný proud je dán elektrickým nábojem, který projde průřezem vodiče za jednu sekundu. Tento náboj se nemůže ve vodiči nikde nahromadit ani vznikat. Všemi průřezy nerozvětveného vodiče prochází týž proud. Dělí-li se proud do několika větví, musí být součet proudů přicházejících do uzlu roven součtu proudů, které z uzlu odcházejí. První Kirchhoffův zákon můžeme vyslovit také následujícím způsobem: Algebraický součet všech proudů v uzlu se rovná nule.

  Druhý Kirchhoffův zákon

  Napětí na každém spotřebiči elektrického obvodu je dáno prací potřebnou k přemístění jednotkového elektrického náboje mezi svorkami spotřebiče. Projde-li náboj po uzavřené dráze, musí být příslušná práce nulová, neboť náboj se vrátil na místo téhož potenciálu. Touto uzavřenou dráhou může být libovolná smyčka v obvodu.

  Druhý Kirchhoffův zákon můžeme vyslovit následujícím způsobem: Algebraický součet všech napětí zdrojů a všech úbytků napětí na spotřebičích se v uzavřené smyčce rovná nule. Případně pokud místo napětí zdrojů budeme uvažovat elekromotorická napětí zdrojů, která mají opačná znaménka, tak můžeme druhý Kirchhoffův zákon formulat také takto: Algebraický součet všech elektromotorických napětí zdrojů v dané uzavřené smyčce obvodu se musí rovnat algebraickému součtu všech úbytků napětí na spotřebičích.

• Rozbor

  Podstata metody uzlových napětí spočívá v tom, že jeden uzel označíme (zvolíme) jako uzel referenční. Volíme takový uzel, ve kterém je spojeno nejvíc prvků. Napětí každého z ostatních uzlů, vztažené k uzlu referenčnímu, označujeme jako napětí uzlové.

  Označíme si proudy jednotlivými větvemi obvodu a aplikujeme na ně první Kirchhoffův zákon. Proudy vyjádříme pomocí uzlových napětí a napětí zdrojů v této větvi.

• Postup řešení

  Naším úkolem je určit proudy: I₁, I₂, I₃, I₄ a napětí: U₁, U₂, U₃, U₄

  

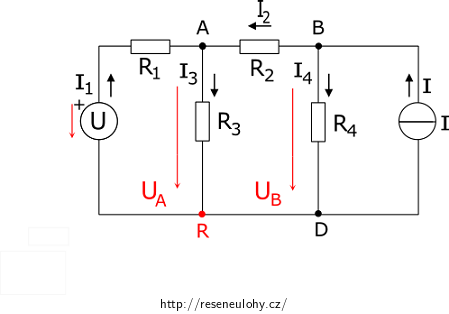
  1. U zdrojů napětí si vyznačíme šipkou směr napětí.

  2. Označíme jednotlivé uzly, přičemž jeden z nich zvolíme jako referenční uzel. V našem případě se jedná o uzel R.

  3. Mezi jednotlivými uzly a uzlem referenčním označíme uzlová napětí. V našem případě jsme je označili jako U_A a U_B.

  4. Označíme si proudy jednotlivými větvemi. Pro každý uzel napíšeme rovnici pomocí prvního Kirchhoffova zákona. Proudy v jednotlivých větvích obvodu vyjádříme pomocí uzlových napětí, napětí zdrojů a odporů rezistorů. Získáme tak soustavu rovnic, kde neznámá jsou uzlová napětí.

  5. Řešením soustavy rovnic najdeme uzlová napětí.

  6.  Pomocí uzlových napětí stanovíme proudy nebo napětí na jednotlivých prvcích obvodu.

• 1. část řešení – sestavení a vyřešení rovnic

  

  V předchozím oddíle je popsán postup řešení, dle něho jsme jako referenční uzel zvolili uzel R, označili uzlová napětí a proudy jednotlivýi větvemi. Teď napíšeme rovnici podle prvního Kirchhoffova zákona pro uzel A:

  \[I_1 + I_2 - I_3\,=\,0 \tag{uzel A}\]

  a pro uzel B:

  \[I - I_2 - I_4\,=\,0. \tag{uzel B}\]

  Proudy větvemi vyjádříme pomocí uzlových napětí a napětí zdrojů:

  \[I_\mathrm{1}\,=\, \frac{U-U_A}{R_1}\,,\] \[I_\mathrm{2}\,=\, \frac{U_B-U_A}{R_2}\,,\] \[I_\mathrm{3}\,=\, \frac{U_A}{R_3}\,,\] \[I_\mathrm{4}\,=\, \frac{U_B}{R_4}\,.\]

  Tyto vztahy dosadíme do výše napsaných rovnic dle prvního Kirchhoffova zákona. Tím získáme dvě rovnice o dvou neznámých:

  \[\frac{U-U_A}{R_1}\,+\frac{U_B-U_A}{R_2}\,-\frac{U_A}{R_3} \,=\, 0,\tag{uzel A}\] \[I-\frac{U_B-U_A}{R_2}\,-\frac{U_B}{R_4} \,=\, 0.\tag{uzel B}\]

  a dosadíme do nich zadané hodnoty v základních jednotkách:

  \[\frac{100-U_A}{100}\,+\frac{U_B-U_A}{200}\,-\frac{U_A}{300} \,=\, 0,\tag{uzel A}\] \[15-\frac{U_B-U_A}{200}\,-\frac{U_B}{400} \,=\, 0.\tag{uzel B}\]

  Rovnice upravíme:

  \[11U_A - 3U_B\,=\,600,\] \[-2U_A + 3U_B\,=\,6000. \]

  Soustavu vyřešíme, například sčítací metodu. První rovnici přičteme ke druhé rovnici:

  \[9U_A\,=\,6600\,.\]

  Tím jsme se zbavili neznáme U_B, vypočítáme U_A:

  \[U_A\,=\, \frac{2200}{3}\,\,\mathrm{V} \dot{=}\,733{,}33\,\,\mathrm{V}.\]

  Nyní dopočítáme i napětí U_B:

  \[-2\frac{2200}{3}\, + 3U_B\,=\,6000, \] \[U_B\,=\, \frac{22400}{9}\,\,\mathrm{V} \dot{=}\,2488{,}88\,\,\mathrm{V}.\]

• 2. část řešení – dopočítání proudů

  Nyní, když jsme si spočítali uzlová napětí, tak proudy spočítáme velice rychle.

  \[I_\mathrm{1}\,=\, \frac{U-U_A}{R_1}\, \Rightarrow\, I_1 \,=\, -\frac{19}{3}\, \mathrm{A}\] \[I_\mathrm{2}\,=\, \frac{U_B-U_A}{R_2}\, \Rightarrow\, I_2 \,=\, \frac{79}{9}\, \mathrm{A}\] \[I_3\,=\,\frac{U_A}{R_3}\, \Rightarrow\, I_3 \,=\, \frac{22}{9}\, \mathrm{A}\] \[I_4\,=\,\frac{U_B}{R_4}\, \Rightarrow\, I_4 \,=\, \frac{56}{9}\, \mathrm{A}\]

• 3. část řešení – dopočítání úbytků napětí

  Úbytky napětí na jednotlivých rezistorech spočítáme pomocí Ohmova zákona:

  \[U_1\,=\, R_1I_1 \Rightarrow\, U_1 \,=\, -\frac{1900}{3}\, \mathrm{V} \dot{=}\,-633{,}33\,\,\mathrm{V}\] \[U_2\,=\, R_2I_2 \Rightarrow\, U_2 \,=\, \frac{15800}{9}\, \mathrm{V} \dot{=}\,1755{,}55\,\,\mathrm{V}\] \[U_3\,=\, R_3I_3 \Rightarrow\, U_3 \,=\, \frac{6600}{9}\, \mathrm{V} \dot{=}\,733{,}33\,\,\mathrm{V}\] \[U_4\,=\, R_4I_4 \Rightarrow\, U_4 \,=\, \frac{22400}{9}\, \mathrm{V} \dot{=}\,2488{,}88\,\,\mathrm{V}\]

• Odpověď

  Spočítali jsme uzlová napětí \(U_A\) a \(U_B\) \[U_A\,=\, \frac{2200}{3}\,\,\mathrm{V} \dot{=}\,733{,}33\,\,\mathrm{V},\] \[U_B\,=\, \frac{22400}{9}\,\,\mathrm{V} \dot{=}\,2488{,}88\,\,\mathrm{V}.\]

  Z uzlových napětích jsme určili proudy

  \[I_1\,=\, -\frac{19}{3}\,\mathrm{A},\qquad \ I_2\,=\, \frac{79}{9}\,\mathrm{A},\qquad \ I_3\,=\, \frac{22}{9}\,\mathrm{A},\qquad \ I_4\,=\, \frac{56}{9}\,\mathrm{A}.\]

  Z proudů jsme určili jednotlivé úbytky napětí

  \[ U_1 \,=\, -\frac{1900}{3}\, \mathrm{V}\ \dot{=}\ -630\,\,\mathrm{V},\] \[ U_2 \,=\, \frac{15800}{9}\, \mathrm{V}\ \dot{=}\ 1\,760\,\,\mathrm{V},\] \[ U_3 \,=\, \frac{2200}{9}\, \mathrm{V}\ \dot{=}\ 730\,\,\mathrm{V},\] \[ U_4 \,=\, \frac{22400}{9}\, \mathrm{V}\ \dot{=}\ 2\,490\,\,\mathrm{V}.\]