Sbírka řešených úloh

Výkon elektrického proudu

Úloha číslo: 42

Ke zdroji s konstantním elektromotorickým napětím je sériově připojen rezistor R₁ o odporu 5 Ω. Poté tento rezistor nahradíme rezistorem R₂ o odporu 0,2 Ω.

Jaký je vnitřní odpor zdroje, jestliže výkon proudu v rezistorech je v obou obvodech stejný?

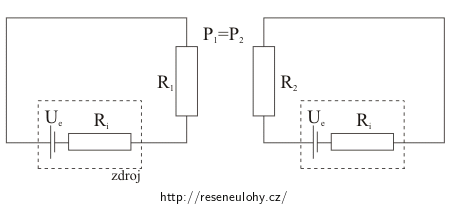
• Nápověda 1

  Uvědomte si nebo vyhledejte, jaký je rozdíl mezi reálným a ideálním zdrojem napětí.

• Řešení nápovědy 1

  Protéká-li obvodem elektrický proud, dochází k úbytku napětí i na zdroji. Můžeme tedy říci, že zdroj klade proudu odpor (tzv. vnitřní odpor zdroje, obvykle ho značíme R_i).

  Ve schématech takový reálný zdroj kreslíme jako ideální zdroj (nemá žádný vnitřní odpor, jeho napětí je rovno elektromotorickému napětí U_e), ke kterému je sériově připojen rezistor o odporu R_i.

  

• Nápověda 2: výkon elektrického proudu v rezistoru

  Uvědomte si, že v obou zapojeních se shoduje výkon elektrického proudu v rezistorech. Tento výkon je roven součinu napětí na rezistoru a proudu, který tímto rezistorem prochází.

• Rozbor

  Protože v našem obvodu je zapojen reálný zdroj, napětí na rezistoru bude rovno rozdílu elektromotorického napětí a napětí na vnitřním odporu zdroje.

  Proud procházející rezistorem vypočítáme z Ohmova zákona pro uzavřený obvod. Ten říká, že proud v uzavřeném obvodu se rovná podílu elektromotorického napětí zdroje a součtu odporů vnější a vnitřní části obvodu (tj. součet odporu R₁ (nebo R₂) a vnitřního odporu zdroje).

  Abychom vypočítali vnitřní odpor zdroje, vyjádříme si pro oba obvody výkon elektrického proudu v rezistoru. Ze zadání úlohy víme, že se tyto výkony rovnají. Jejich porovnáním získáme hledaný vnitřní odpor zdroje.

• Řešení

  Výkon elektrického proudu na připojeném rezistoru vypočítáme ze vztahu

  \[P\,=\,UI\,=\,\left(U_\mathrm{e}-R_\mathrm{i}I\right)I\,,\]

  kde U_e je elektromotorické napětí, R_i je vnitřní odpor zdroje a I je proud protékající obvodem.

  Jestliže je výkon proudu P pro oba rezistory stejný, pak platí, že

  \[P_1\,=\,U_\mathrm{e}I_1-R_\mathrm{i}I_1^2\] \[P_2\,=\,U_\mathrm{e}I_2-R_\mathrm{i}I_2^2\] \[P_1\,=\,P_2\,,\]

  a tedy

  \[U_\mathrm{e}I_1-R_\mathrm{i}I_1^2\,=\,U_\mathrm{e}I_2-R_\mathrm{i}I_2^2\,.\]

  Z této rovnice si vyjádříme vnitřní odpor R_i:

  \[U_\mathrm{e}\left(I_1-I_2\right)\,=\,R_\mathrm{i}\left(I_1^2-I_2^2\right)\] \[R_\mathrm{i}\,=\,\frac{U_\mathrm{e}\left(I_1-I_2\right)}{I_1^2-I_2^2} \,=\,\frac{U_\mathrm{e}\left(I_1-I_2\right)}{\left(I_1-I_2\right)\left(I_1+I_2\right)} \,=\,\frac{U_\mathrm{e}}{I_1+I_2}\,.\tag{1}\]

  Z Ohmova zákona pro uzavřený obvod víme, že

  \[I\,=\,\frac{U_\mathrm{e}}{R+R_\mathrm{i}}\,.\]

  V našem případě to znamená:

  \[I_1\,=\,\frac{U_\mathrm{e}}{R_1+R_\mathrm{i}}\hspace{20px} I_2\,=\,\frac{U_\mathrm{e}}{R_2+R_\mathrm{i}}\,.\tag{1. a 2. obvod}\]

  Takto vyjádřené neznámé proudy I₁, I₂ dosadíme do rovnice (1) a upravíme:

  \[R_\mathrm{i}\,=\,\frac{U_\mathrm{e}}{\frac{U_\mathrm{e}}{R_1+R_\mathrm{i}}+\frac{U_\mathrm{e}}{R_2+R_\mathrm{i}}} \,=\,\frac{1}{\frac{1}{R_1+R_\mathrm{i}}+\frac{1}{R_2+R_\mathrm{i}}}\] \[ R_\mathrm{i}\,=\,\frac{\left(R_1+R_\mathrm{i}\right)\left(R_2+R_\mathrm{i}\right)} {\left(R_2+R_\mathrm{i}\right)+\left(R_1+R_\mathrm{i}\right)}\,.\]

  V této rovnici nám zbyla jediná neznámá R_i, kterou vyjádříme:

  \[R_\mathrm{i}\left(R_1+R_2+2R_\mathrm{i}\right)\,=\,R_1R_2+R_\mathrm{i}R_1+R_\mathrm{i}R_2+R_\mathrm{i}^2\] \[2R_\mathrm{i}^2\,=\,R_1R_2+R_\mathrm{i}^2\] \[R_\mathrm{i}^2\,=\,R_1R_2\] \[R_\mathrm{i}\,=\,\sqrt{R_1R_2}\,.\]

• Odpověď

  Je-li výkon proudu pro dva rezistory o odporu R₁ = 5 Ω a R₂ = 0,2 Ω ve vnější části obvodu stejný, pak vnitřní odpor zdroje je \(R_\mathrm{i}\,=\,\sqrt{R_1R_2}\,=\,\sqrt{5 {\cdot} 0{,}2}\,\mathrm{\Omega}\,=\,1\,\mathrm{\Omega}\).

• Odkaz na podobnou úlohu

  Podívejte se také na úlohu Výpočet proudů v obvodu při konstantním výkonu.