Sbírka řešených úloh

Indukce bez vodiče

Úloha číslo: 255

• Nápověda 1

  Použijte Maxwellovu rovnici vyjadřující Faradayův zákon v integrálním tvaru

  \[\oint_\mathrm{c} \vec E\cdot \mathrm{d}\vec l = -\frac{\mathrm{d}\Phi}{\mathrm{d}t},\]

  přičemž integrál vlevo (odpovídající indukovanému napětí) počítáme přes nějakou uzavřenou smyčku c v prostoru a člen vpravo vyjadřuje časovou změnu indukčního toku plochou této smyčky.

• Nápověda 2

  Otázkou je, jak vhodně volit smyčku, aby integrál v Maxwellově rovnici (viz předchozí nápověda) byl „jednoduše“ spočitatelný.

  Za tím účelem odvoďte, že vektor elektrické intenzity rotuje kolem osy válce (podobně jako vektor magnetické indukce rotuje kolem tenkého přímého vodiče s proudem) a velikost elektrické intenzity závisí pouze na vzdálenosti od osy válce.

  Vhodnou smyčkou bude tedy kruhová smyčka obepínající osu válce.

  Vyjádřete pak také časovou derivaci indukčního toku pomocí plochy této smyčky a časové derivace magnetické indukce.

• Rozbor

  Proměnné magnetické pole indukuje pole elektrické podle Faradayova zákona elektromagnetické indukce. V úlohách se obvykle používá na smyčky tvořené vodiči. Pro tuto úlohu je důležité si uvědomit, že není nijak podstatné, že žádné vodiče nejsou přítomny. Indukované elektrické pole vzniká stejně.

  Pro výpočet elektrického pole tak můžeme využít Faradayův zákon; tentokrát ovšem ve verzi s intenzitou pole, tedy vlastně přímo jednu z Maxwellových rovnic v integrálním tvaru \[\oint_\mathrm{c} \vec E\cdot\mathrm{d}\vec l = -\frac{\mathrm{d}\Phi}{\mathrm{d}t}.\] Vlevo můžeme integrovat přes libovolnou uzavřenou smyčku c. Abychom integrál spočetli, musíme tuto smyčku zvolit vhodným způsobem. Vzhledem k válcové symetrii se vhodnou volbou jeví být kružnice se středem v ose válce a ležící v jeho kolmém řezu: vektor intenzity elektrického pole totiž musí být v každém místě kolmý na vektor magnetické indukce (to vyplývá přímo z Maxwellových rovnic a platí pro každé elektromagnetické pole), bude tedy ležet v rovině kolmého řezu válce.

  Dokonce je pravda, že v každém bodě kružnice bude mít stejnou velikost a také bude mít směr tečny ke kružnici v tomto bodě; podrobné zdůvodnění je ponecháno do řešení úlohy.

  V takovém případě můžeme integrál vlevo a také změnu indukčního toku smyčkou lehko spočítat.

• Řešení – Faradayův zákon

  Využijeme integrální tvar Faradayova zákona, který říká, že

  \[\oint_\mathrm{c} \vec{E}\cdot {\rm d}\vec l = -\frac{{\rm d}\Phi}{{\rm d}t}.\tag{1}\]

  Na levé straně je vlastně elektromotorické napětí vzniklé v nějaké křivce c, kterou můžeme volit libovolně, musí však být uzavřená. Přitom nezáleží na tom, zda tato křivka představuje fyzicky přítomný vodič; elektrické pole vznikne tak jako tak! V uzavřeném vodiči se pouze navíc projeví vznikem indukovaného proudu.

  Můžeme si tedy libovolně zvolit uzavřenou křivku, podél níž budeme integrovat levou stranu. Vhodnou volbou křivky c je kružnice (o poloměru r < R) ležící v kolmém řezu válce se středem v ose válce. Vektor elektrické intenzity \(\vec{E}\) bude ležet v rovině této kružnice (musí být kolmý na vektor \(\vec{B}\)). Ze symetrie situace pak vyplývá, že tento vektor bude v každém bodě tečný ke kružnici.

   

  To si zaslouží podrobnější komentář. Zdůvodnění lze nalézt několik, tady se pokusíme vyhnout diferenciálním operátorům a nabídnout fyzikální pohled. Válcová symetrie situace nám totiž zaručuje jedinou věc, a to sice, že pokud by vektor \(\vec{E}\) byl odchýlený od tečny, pak bude „stejně odchýlený“ od tečny ve všech bodech kružnice. Pak bychom intenzitu mohli rozdělit na dvě složky: tečnou ke kružnici a normálovou. Z důvodu symetrie je ale normálová složka nulová a vektor \(\vec{E}\) tečný ke kružnici.

  Pokud by normálová složka nebyla nulová, mohli bychom si představit vodič ve směru normálové složky, tato složka elektrické intenzity by v něm vyvolala proud a ten by vyvolal magnetické pole, které by ovšem cirkulovalo kolem tohoto vodiče. Přitom není nijak podstatné, že tam tento vodič fyzicky není — elektrické pole vyvolává magnetické pole, vodič k tomu není potřeba. Takové magnetické pole však podle zadání úlohy není přítomno.

   

  Shrňme, že ze symetrie víme: vektor elektrické intenzity v každém bodě kružnice má stejnou velikost E a je k ní tečný. Integrál na levé straně rovnice (1) je tedy roven

  \[\oint_\mathrm{c} \vec E\cdot {\rm d}\vec l = \oint_\mathrm{c} E\,{\rm d}l = E \oint_\mathrm{c} {\rm d}l = E \ (2\pi r).\]

  Na pravé straně rovnice (1) je časová derivace indukčního toku skrze kruh určený touto kružnicí. Vzhledem k rovnoběžnosti vektorů \(\vec{B}\) a \(\vec{S}\) a neměnnosti plochy kruhu S máme:

  \[-\frac{{\rm d}\Phi}{{\rm d}t} = -S\frac{{\rm d}B}{{\rm d}t} = -\pi r^2\frac{{\rm d}B}{{\rm d}t}.\]

  Porovnáním předchozích vztahů dostaneme

  \[E\cdot (2\pi r) = -\pi r^2\frac{{\rm d}B}{{\rm d}t},\] \[E = -\frac{r}{2}\frac{{\rm d}B}{{\rm d}t}.\]

  Znaménko minus značí fakt, že indukované pole se snaží zabránit změně, která jej vyvolala. Souvisí tedy se směrem, nikoli s velikostí elektrické intenzity.

• Řešení – orientace indukovaného pole

  Už jsme řekli, že směr elektrické intenzity je tečný ke kružnici. Jak je orientován? Předpokládejme, že magnetické pole roste. Potom pole na kružnici musí cirkulovat takovým směrem, aby v myšlené proudové smyčce obíhal takový proud, který vyvolá magnetické pole ve středu smyčky směrem dolů.

  Podle Ampérova pravidla pravé ruky pak vyplývá, že intenzita „obíhá“ kružnici po směru hodinových ručiček.

  

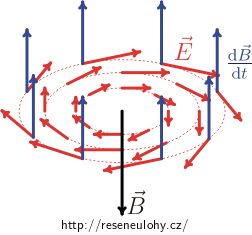
  K obrázku výše upozorněme, že modré šipky neznázorňují magnetickou indukci \(\vec B\), ale její časovou derivaci! Magnetickou indukci \(\vec B\), vyvolanou elektrickým polem, znázorňuje pro přehlednost jediný černý vektor. Modrý vektor mířící vzhůru nám tedy naznačuje, že magnetické pole roste (neboť podle zadání magnetická indukce uvnitř válce míří vzhůru). Červené šipky pak mají význam vektoru intenzity elektrického pole \(\vec E\) v daném místě.

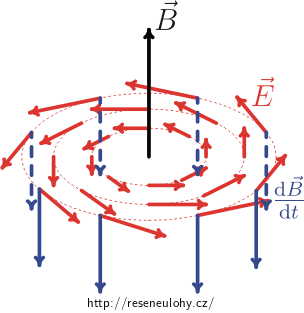
  Pro úplnost dodejme, že pokud by magnetické pole sláblo, pak by „modrý“ vektor časové derivace magnetické indukce mířil dolů a vektor intenzity elektrického pole by obíhal kolem osy válce v opačném smyslu, tedy proti směru hodinových ručiček. Magnetickou indukci \(\vec B\), vyvolanou elektrickým polem, opět znázorňuje černý vektor (viz obrázek níže).

  

• Odpověď

  Pokud velikost magnetické indukce roste, vektor intenzity elektrického pole rotuje kolem osy po směru hodinových ručiček.

  Pokud velikost magnetické indukce klesá, vektor intenzity elektrického pole rotuje kolem osy proti směru hodinových ručiček.

  V obou případech je jeho velikost přímo úměrná vzdálenosti r od osy otáčení:

  \[E = \frac{r}{2}\frac{{\rm d}B}{{\rm d}t}.\]