Nekonečná síť rezistorů

Úloha číslo: 665

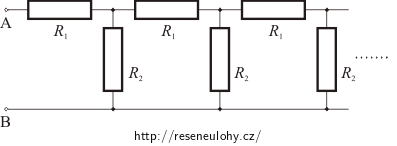
Na obrázku je nakreslena nekonečná rezistorová síť s rezistory o odporech R₁ a R₂. Určete celkový odpor sítě.

Nápověda 1
Zamyslete se, jak se změní celkový odpor sítě, jestliže k ní přidáme ještě jeden „kousek“ (tedy jeden sériově a jeden paralelně zapojený rezistor) nebo ho naopak ubereme.
Řešení nápovědy 1
Uvažovaná síť rezistorů je nekonečná, proto přidáme-li k této síti ještě jeden „kousek“, bude jich tam stále nekonečně mnoho a celkový odpor se nezmění. To nám umožní celé zapojení překreslit do velmi jednoduché náhradní sítě, jejíž odpor musí být roven celkovému odporu původní nekonečné sítě R_AB.
Nápověda 2
Uvědomte si, jaká pravidla platí pro počítání celkového odporu sériově a paralelně zapojených rezistorů.
Řešení nápovědy 2
Při sériovém spojení n rezistorů je celkový odpor roven součtu odporů jednotlivých rezistorů:
\[ R\,=\,R_1\,+\,R_2\,+\,...\,+\,R_\mathrm{n}. \]
Při paralelním zapojení n rezistorů platí, že převrácená hodnota celkového odporu je rovna součtu převrácených hodnot odporů jednotlivých rezistorů:
\[ \frac{1}{R}\,=\,\frac{1}{R_1}\,+\,\frac{1}{R_2}\,+\,...\,+\,\frac{1}{R_\mathrm{n}}. \]
Nápověda 3
Při řešení úlohy bude potřeba vyřešit kvadratickou rovnici. Uvědomte si nebo vyhledejte, jak se kvadratická rovnice řeší.
Řešení nápovědy 3
Kvadratická rovnice ax² + bx + c = 0 s neznámou x a koeficienty a, b, c, má dva kořeny.

Tyto kořeny určíme ze vztahu:
\[ x_{1{,}2}\,=\,\frac{-b\,\pm\,\sqrt{b^2-4ac}}{2a}\,. \]
Rozbor
V této úloze je pro nás velmi důležitou skutečností, že uvažovaná síť rezistorů je nekonečná.

Přidáme-li tedy k této síti ještě jeden člen, což je v našem případě jeden sériově a jeden paralelně zapojený rezistor, celkový odpor se nezmění. To nám umožní celé zapojení překreslit do velmi jednoduché náhradní sítě, jejíž odpor musí být roven celkovému odporu původní nekonečné sítě R_AB.

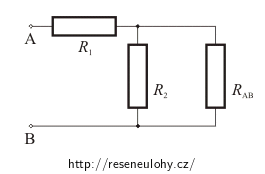
Pomocí pravidel pro výpočet celkového odporu pro paralelně a sériově zapojené rezistory nyní můžeme odpor sítě R_AB vypočítat.
Řešení
Rezistorová síť ze zadání úlohy je nekonečná. Přidáme-li tedy k této síti ještě jeden člen (jeden sériově a jeden paralelně zapojený rezistor), celkový odpor se nezmění. Celé zapojení tedy můžeme překreslit do sítě, jejíž odpor musí být roven celkovému odporu původní nekonečné sítě R_AB.

Pomocí pravidel pro výpočet celkového odporu pro paralelně a sériově zapojené rezistory nyní vypočítáme odpor sítě R_AB.

Celkový odpor paralelně zapojených rezistorů R₂ a R_AB označíme R_p (v obrázku vyznačen červeně).

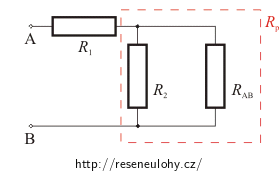
Pro odpor R_p tedy platí:
\[ \frac{1}{R_\mathrm{p}}\,=\,\frac{1}{R_2}+\frac{1}{R_\mathrm{AB}}\,=\,\frac{R_\mathrm{AB}+R_2}{R_2R_\mathrm{AB}} \] \[ R_\mathrm{p}\,=\,\frac{R_2R_\mathrm{AB}}{R_\mathrm{AB}+R_2}\,. \]
Celkový odpor nekonečné rezistorové sítě R_AB se rovná součtu odporů R₁ a R_p (tyto rezistory jsou zapojeny sériově):
\[ R_\mathrm{AB}\,=\,R_1\,+\,R_\mathrm{p}\,=\,R_1\,+\,\frac{R_2R_\mathrm{AB}}{R_\mathrm{AB}+R_2} \] \[ R_\mathrm{AB}\,=\,\frac{R_1\left(R_\mathrm{AB}+R_2\right)+R_2R_\mathrm{AB}}{R_\mathrm{AB}+R_2}\,. \]
Nyní za pomoci matematických úprav vypočítáme odpor R_AB:
\[ R_\mathrm{AB}\left(R_\mathrm{AB}+R_2\right)\,=\,R_1\left(R_\mathrm{AB}+R_2\right)+R_2R_\mathrm{AB} \] \[ R_\mathrm{AB}^2\,+\,R_2R_\mathrm{AB}\,=\,R_1R_\mathrm{AB}\,+\,R_1R_2\,+\,R_2R_\mathrm{AB} \] \[ R_\mathrm{AB}^2\,=\,R_1R_\mathrm{AB}\,+\,R_1R_2 \] \[ R_\mathrm{AB}^2\,-\,R_1R_\mathrm{AB}\,-\,R_1R_2\,=\,0\,. \]
Získali jsme tedy kvadratickou rovnici pro neznámou R_AB. Vyřešením této rovnice již určíme celkový odpor nekonečné sítě:
\[ R_\mathrm{AB}\,=\,\frac{R_1\,+\sqrt{R_1^2+4R_1R_2}}{2}\,=\,\frac{R_1\,+\,\sqrt{R_1^2\left(1+\frac{4R_2}{R_1}\right)}}{2} \] \[ R_\mathrm{AB}\,=\,\frac{R_1\,+\,R_1\sqrt{1+\frac{4R_2}{R_1}}}{2} \] \[ R_\mathrm{AB}\,=\,\frac{R_1}{2}\left(1\,+\,\sqrt{1+\frac{4R_2}{R_1}}\right). \]
Druhé řešení kvadratické rovnice vychází záporně, což je pro nás nepřijatelné.
Odpověď
Odpor nekonečné sítě rezistorů je dán vztahem
\[ R_\mathrm{AB}\,=\,\frac{R_1}{2}\left(1\,+\,\sqrt{1+\frac{4R_2}{R_1}}\right). \]
Odkazy na podobné úlohy
Zkuste si vyřešit také úlohy Odpor elektrické sítě, Netradiční obvody 1 a Netradiční obvody 2.