Sbírka řešených úloh

Kuličky na niti ponořené do benzenu

Úloha číslo: 26

• Nápověda 1

  Jaké síly na kuličky působí a co pro tyto síly musí platit?

  Nakreslete si obrázek.

• Nápověda 2

  Které síly se změní, ponoříme-li kuličky do benzenu? Přibudou nějaké nové síly?

• Obrázek

  

  

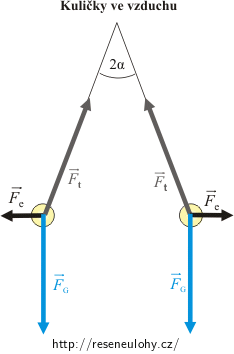
• Rozbor

  Na vzduchu na každou nabitou kuličku zavěšenou na vlákně působí tíhová síla, tahová síla vlákna a odpudivá elektrická síla. Obě kuličky jsou v klidu, proto výslednice všech tří sil musí být nulová.

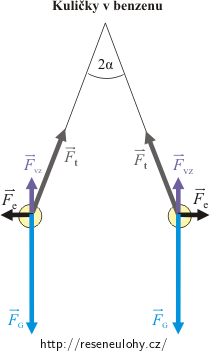
  Ponoříme-li kuličky do benzenu, některé působící síly se změní, ale výslednice sil musí být opět rovna nule.

  Odpudivá elektrická síla se ε_r-krát zmenší a změní se také tahová síla vlákna. Tíhová síla zůstane stejná. Navíc přibude vztlaková síla.

  V obou případech si z vhodného pravoúhlého trojúhelníka můžeme vyjádřit tangens úhlu α, oba vztahy porovnat a vyjádřit odtud neznámou hustotu.

  

  

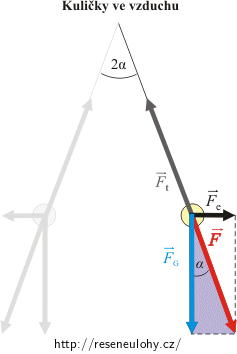
• Řešení

  Na vzduchu působí na každou kuličku tíhová síla \(\vec{F}_\mathrm{G}\) a tahová síla vlákna \(\vec{F}_\mathrm{t}\). Protože jsou kuličky nabité, odpuzují se navzájem elektrickou silou \(\vec{F}_\mathrm{e}\).

  Pro velikost sil platí:

  \[F_\mathrm{G}\,=\,mg,\] \[F_\mathrm{e}\,=\,\frac{1}{4 \pi \varepsilon_0}\, \frac{Q^2}{r^2}\,,\]

  kde r je vzdálenost kuliček.

  Vzhledem k tomu, že jsou kuličky v klidu, je výslednice těchto tří sil rovna nule.

  Z „fialového“ pravoúhlého trojúhelníka můžeme vyjádřit tangens úhlu α:

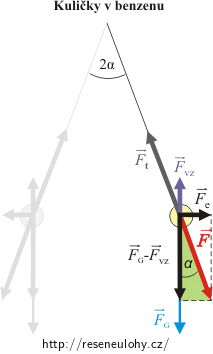
  \[\mathrm{tg}\, \alpha=\frac{F_\mathrm{e}}{F_\mathrm{G}}\,=\,\frac{\frac{1}{4 \pi \varepsilon_0}\, \frac{Q^2}{r^2}}{mg},\] \[\mathrm{tg}\, \alpha\,=\,\frac{1}{4 \pi \varepsilon_0} \,\frac{Q^2}{mgr^2}.\tag{*}\]

  Ponoříme-li kuličky do benzenu, přibude navíc čtvrtá síla — vztlaková síla \(\vec{F}_\mathrm{VZ}\). Tíhová síla zůstane stále stejná, ale odpudivá elektrická síla \(\vec{F}_\mathrm{e}\) se ε_r-krát zmenší. Změní se také tahová síla vlákna:

  \[F_\mathrm{G}\,=\,mg,\] \[F_\mathrm{e}\,=\,\frac{1}{4 \pi \varepsilon_0 \varepsilon_r}\, \frac{Q^2}{r^2}, \] \[F_\mathrm{VZ}\,=\,V \varrho_b g.\]

  Výslednice všech čtyř sil musí být opět nulová.

  Znovu si vyjádříme tg α, tentokrát ze „zeleného“ trojúhelníka:

  \[\mathrm{tg}\, \alpha\,=\,\frac{F_\mathrm{e}}{F_\mathrm{G}-F_\mathrm{VZ}}\,=\,\frac{\frac{1}{4 \pi \varepsilon_0 \varepsilon_r}\, \frac{Q^2}{r^2}}{mg-V \varrho_b g}, \] \[\mathrm{tg}\, \alpha\,=\,\frac{1}{4 \pi \varepsilon_0 \varepsilon_r}\, \frac{Q^2}{r^2\left(mg-V \varrho_b g \right)}.\tag{**}\]

  Nyní oba vztahy (*) a (**) pro tangens úhlu α porovnáme:

  \[\frac{1}{4 \pi \varepsilon_0} \,\frac{Q^2}{mgr^2} \,=\,\frac{1}{4 \pi \varepsilon_0 \varepsilon_r}\, \frac{Q^2}{r^2g\left(m-V \varrho_b \right)}.\]

  Obě strany rovnice vynásobíme \(4 \pi \varepsilon_0 gr^2\) a vydělíme Q²:

  \[\frac{1}{m} \,=\,\frac{1}{ \varepsilon_r}\, \frac{1}{m-V \varrho_b }\,.\]

  Za hmotnost kuličky m můžeme dosadit m = V ρ a dostaneme:

  \[\frac{1}{V\varrho}\, =\,\frac{1}{ \varepsilon_r}\, \frac{1}{V\varrho-V \varrho_b }.\]

  Z této rovnice vyjádříme neznámou hustotu kuličky ρ.

  \[\frac{1}{\varrho}\,=\,\frac{1}{ \varepsilon_r}\, \frac{1}{\varrho-\varrho_b },\] \[\varrho\,=\,\varepsilon_r \left(\varrho-\varrho_b \right).\]

  Závorku roznásobíme a členy s neznámou převedeme na levou stranu:

  \[\varepsilon_r \varrho-\varrho\,=\,\varepsilon_r \varrho_b,\] \[\varrho \left(\varepsilon_r -1\right)\,=\,\varepsilon_r \varrho_b,\] \[\varrho\,=\,\frac{\varrho_b \varepsilon_r }{\varepsilon_r -1}.\]

• Zápis a číselné dosazení

  ρb = 879 kg m−3	hustota benzenu
  εr = 2,3	relativní permitivita benzenu
  ρ = ?  ( kg m−3)	hustota kuliček

  ---

  \[\varrho\,=\,\frac{\varrho_b \varepsilon_r }{\varepsilon_r -1}\,=\,\frac{2{,}3 \,\cdot\, 879}{2{,}3-1}\,\mathrm{kg\,m^{-3}}\dot=\,1\,600\,\mathrm{kg\,m^{-3}}\]

  Podíváme-li se do tabulek, zjistíme, že kuličky jsou nejspíš vyrobeny z nějaké umělé hmoty.

• Odpověď

  Kuličky jsou vyrobeny z látky o hustotě \(\varrho=\frac{\varrho_b \varepsilon_r }{\varepsilon_r -1}\dot=1\, 600\,\mathrm{kg\,m^{-3}}\).

• Odkaz na jednodušší úlohu

  Úloha, ve které jsou kuličky zavěšené pouze ve vzduchu, má název Zavěšené nabité kuličky.