Galvanometr
Úloha číslo: 311
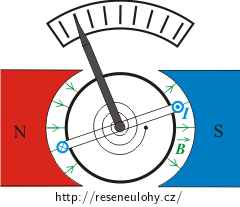
Obdélníková smyčka galvanometru má 50 závitů. Strana cívky rovnoběžná s nákresnou má délku 3,0 cm, strana cívky kolmá k nákresně má délku 2,0 cm. Cívka je umístěna v radiálním magnetickém poli o magnetické indukci 0,010 T. Torzní konstanta vlasového pera, na němž je cívka zavěšena, je 1,0·10 -8 Nm/° .
a) Nakreslete vektory magnetických sil působících na strany cívky, které jsou kolmé k nákresně. Směr proudu je vyznačen na obrázku.
b) Určete ustálenou výchylku φ galvanometru, jestliže závity prochází proud 1,0 mA.
c) Diskutujte, co se stane, když proud, který prochází cívkou galvanometru, změní směr.
Nápověda
Jestliže se cívka, kterou prochází elektrický proud, nachází v magnetickém poli, začnou na její strany působit magnetické síly. Směr těchto sil určíme pomocí Flemingova pravidla levé ruky.
Magnetické síly působící na strany cívky zapříčiní, že se cívka začne v magnetickém poli otáčet podle své osy. Aby se cívka neotáčela, ale pouze vychýlila z rovnovážné polohy, působí na ni pružina. V rovnovážném stavu se moment magnetické síly rovná silovému momentu, kterým na cívku působí pružina.
Nápověda - Torzní moment a torzní konstanta
Torzní kyvadlo (viz obrázek) je dalším příkladem kmitavého systému. Jestliže pootočíme disk vzhledem k jeho rovnovážné poloze a pak uvolníme, začne na něm nakreslená ryska kmitat kolem rovnovážné polohy — dojde k tzv. torzním kmitům. Při úhlové výchylce φ, v libovolném z obou směrů, vzniká vratný silový moment, kterým působí zkroucené zavěšené vlákno (tzv. torzní moment). Pro jeho velikost platí:
\[M=-\kappa \varphi.\]Konstanta κ se jmenuje torzní konstanta. Její velikost závisí na délce zavěšeného vlákna, na jeho průměru a na materiálu, z něhož je vlákno vyrobeno.
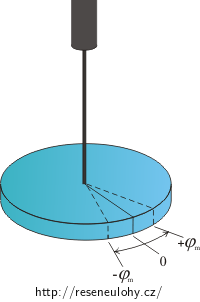
Stejným způsobem, jako u torzních kmitů, je charakterizováno i silové působení pružiny na ručičku přístroje. Torzní konstanta pružiny je tedy konstantou úměrnosti mezi velikostí silového momentu pružiny a úhlem vychýlení ručičky.
Rozbor
Měření proudu v galvanometrech s pohyblivou cívkou je založeno na rotačním účinku magnetického pole na smyčku, kterou protéká proud.
Mezi permanentními magnety je umístněna cívka navinutá na jádro z měkkého feromagnetického materiálu. Tvar permanentních magnetů a jádra způsobuje, že magnetická indukce v prostoru mezi permanentními magnety a jádrem má radiální směr (viz obrázek v zadání).
Jestliže cívkou, nacházející se v magnetickém poli, začne procházet elektrický proud, působí na ní díky konstrukci galvanometru dvojice magnetických sil, která způsobí otočení cívky v magnetickém poli a tím i vychýlení ručičky na stupnici, která je s cívkou spojena. Aby se cívka v magnetickém poli nezačala otáčet, ale došlo jen k výchylce z rovnovážné polohy úměrné velikosti proudu, je k cívce přidělána pružinka, která působí silou, jejíž moment vyrovnává moment magnetické síly. Silový moment, kterým pružinka působí je úměrný výchylce z rovnovážné polohy.
Směr působících magnetických sil a smysl rotace
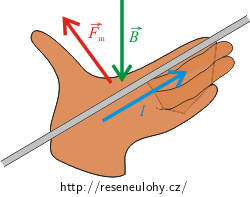
Směr magnetických sil působících na cívku, kterou prochází proud, určíme pomocí Flemingova pravidla levé ruky, jež říká:
Položíme-li k vodiči levou ruku tak, aby natažené prsty ukazovaly směr proudu a magnetické indukční čáry (respektive vektor \(\vec{B}\)) vstupovaly do dlaně, ukazuje odtažený palec směr a orientaci vektoru magnetické síly \(\vec{F}_\mathrm{m}\), která působí na vodič.
Jestliže cívkou prochází proud vyznačený na obrázku v zadání, působí na cívku dvojice magnetických sil. Ty způsobí, že se cívka v magnetickém poli vychýlí proti směru hodinových ručiček (v kladném smyslu), tj. dojde k vychýlení ručičky přístroje doleva.
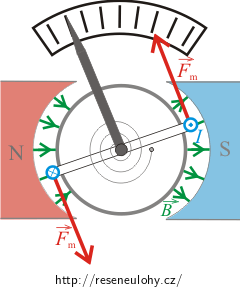
Poznámka: Na strany závitu cívky rovnoběžné s obrázkem magnetická síla nepůsobí, protože jsou rovnoběžné s vektorem magnetické indukce \(\vec{B}\).
Po zapojení galvanometru do obvodu obráceně, začne cívkou procházet proud v opačném směru. Magnetické síly působící na cívku tedy budou mít směr po směru hodinových ručiček a ručička galvanometru se vychýlí doprava.
Pokud bude galvanometr zapojený v obvodu se střídavým proudem s malou frekvencí, bude dvojice magnetických sil neustále měnit svůj směr. Ručička galvanometru se tak neustálí na jedné hodnotě, ale bude kmitat s amplitudou rovnou maximální výchylce proudu. Pokud ale frekvence střídavého proudu bude příliš vysoká, ručička díky své hmotnosti “nebude stíhat“ s takto vysokou frekvencí kmitat a zůstane stát uprostřed.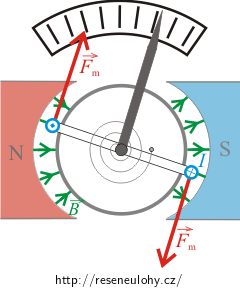
Řešení
Při průchodu proudu cívkou v magnetickém poli začnou na strany cívky působit magnetické síly. Ty způsobí, že se cívka začne otáčet podle své osy. Aby se cívka v magnetickém poli stále neotáčela, ale pouze se vychýlila ze své rovnovážné polohy, úměrně velikosti proudu, který jí protéká, je k ní přidělána pružina. Velikost magnetických sil, a tedy i jejich moment, je úměrný protékajícímu proudu. Moment síly pružiny je úměrný úhlu natočení cívky. To znamená, že výchylka cívky je úměrná protékajícímu proudu.
Položíme-li velikost momentu magnetické síly M rovnu velikosti silového momentu M' vyvolaného pružinou, dostáváme
\[M=M'.\]Pro vyjádření velikosti momentu magnetické síly M vyšetříme síly, které působí na jednotlivé strany obdélníkové cívky umístěné v magnetickém poli.
Velikosti sil působících na jednotlivé strany obdélníkové smyčky určíme pomocí vztahu
\[F_\mathrm{m}=I|\vec{l}\times\vec{B}|=IlB\sin\alpha,\]kde úhel α je úhel mezi vektorem magnetické indukce \(\vec{B}\) a směrem proudu.
Magnetické síly působící na strany cívky rovnoběžné s obrázkem
Díky tomu, že je magnetické pole, v němž se nachází cívka, radiální, nepůsobí na strany cívky rovnoběžné s obrázkem žádné síly. Vektor magnetické indukce je totiž vždy rovnoběžný se směrem proudu v těchto stranách cívky.
Magnetické síly působící na strany cívky kolmé k obrázku
Směr proudu procházejícího částí cívky, která je kolmá k obrázku, svírá se směrem vektoru magnetické indukce pravý úhel, tj. α = 90°. Pro velikost magnetické síly působící na vodič délky b platí
\[F_1=F_2=IbB\sin 90^{\circ}=IbB.\]Síly jsou rovnoběžné a vzájemně opačně orientované.
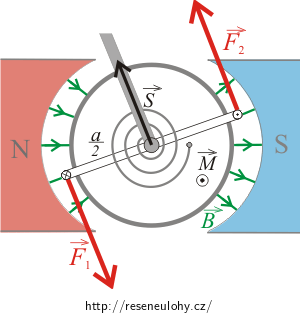
Momenty obou sil mají stejný směr, jsou kolmé k rovině určené oběma silami a celkový moment má velikost
\[M=F_1\frac{a}{2}+F_2\frac{a}{2}=\frac{a}{2} (F_1+F_2).\]Protože síly F1 a F2 mají stejnou velikost, můžeme psát
\[M=\frac{a}{2} (F_1+F_2)=F_1 a=IabB=ISB,\]kde jsme dosadili obsah závitu cívky S = ab. Výsledný silový moment působící na cívku o N závitech má velikost
\[M=NISB.\]Pro velikost silového momentu M' vyvolaného pružinou platí
\[M'=\kappa \varphi,\]kde κ je torzní konstanta a φ je úhlová výchylka.
Položíme-li velikost momentu magnetické síly M rovnu velikosti silového momentu M' vyvolaného pružinou, dostáváme
\[NISB=\kappa \varphi.\]Pro výchylku φ galvanometru platí
\[\varphi=\frac{NISB}{\kappa}.\]Zápis a číselné dosazení
\(N=50\) počet závitů smyčky galvanometru \(a=3{,}0\,\mathrm{cm}=0{,}030\,\mathrm{m}\) délka strany cívky rovnoběžné s nákresnou \(b=2{,}0\,\mathrm{cm}=0{,}020\,\mathrm{m}\) délka strany cívky kolmé k nákresně \(B=0{,}010\,\mathrm{T}\) magnetická indukce pole cívky \(\kappa=1{,}0{\cdot} 10^{-8}\,\mathrm{Nm/^{\circ}}\) torzní konstanta vlasového pera \(I=1{,}0\,\mathrm{mA}=1{\cdot} 10^{-3}\,\mathrm{A}\) proud procházející závity galvanometru \(\varphi=?\,\mathrm{(^{\circ})}\) výchylka galvanometru
\[\varphi=\frac{NISB}{\kappa}=\frac{50{\cdot} 10^{-3}\cdot0{,}03{\cdot}0{,}02{\cdot}0{,}01}{1{,}0{\cdot} 10^{-8}}=30^{\circ}\]Odpověď
Výchylka galvanometru se při průchodu proudu o velikosti 1,0 mA ustálila na φ = 30°.
Pokud cívkou začne procházet proud opačným směrem, magnetické síly působící na cívku změní svůj směr a ručička galvanometru se vychýlí na druhou stranu.






