Magnetické pole rotující nabité koule
Úloha číslo: 243
Vypočtěte vektorový potenciál magnetického pole koule o poloměru R rotující úhlovou rychlostí ω kolem osy procházející jejím středem. Na povrchu koule je rovnoměrně rozložen povrchový náboj s hustotou σ. Vypočtěte také magnetickou indukci uvnitř a vně této koule.
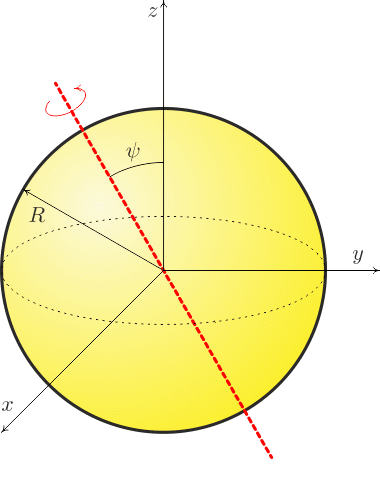
Osa rotace leží v rovině xz a s osou z svírá úhel ψ.
Nápověda 1
Nic se nezmění, pokud si kouli představíme stojící a necháme po ní obíhat pouze náboj. Pohybující se náboj na kouli pak vlastně představuje proud tekoucí po jejím povrchu, tj. plošný proud.
Jaká bude jeho plošná hustota \(\vec k\) v místě \(\vec r^,\), kde se náboj pohybuje rychlostí \(\vec v\)? A jak souvisí s vektorem úhlové rychlosti \(\vec\omega\) rotace koule?
Nápověda 2
Připomeňte si vztah pro výpočet vektorového potenciálu \(\vec A\) v místě \(\vec r\) buzeného plošným proudovým elementem \(\vec k\) v místě \(\vec r^,\).
Rozbor
Rotující koule s povrchovou hustotou náboje σ se chová stejně jako stojící koule, po jejímž povrchu teče proud o plošné hustotě \(\vec k\):
\[\vec k = \sigma\vec v.\]Proudový element \(\mathrm{d}\vec I\) v místě \(\vec r^,\) budí v místě \(\vec r\) vektorový potenciál
\[\mathrm{d}\vec A(\vec r) = \frac{\mu_0}{4\pi}\frac{\mathrm{d}\vec I}{|\vec r-\vec r^,|}.\]Integrací přes plochu koule tak dostáváme vztah
\[\vec A(\vec r) = \frac{\mu_0}{4\pi}\int \frac{\vec k(\vec r^,)\,\mathrm{d}S^,}{|\vec r-\vec r^,|}.\]Tento integrál je třeba spočítat. Jeden z možných postupů je využít sférické souřadnice.
Z vektorového potenciálu ihned aplikací operátoru rotace určíme magnetickou indukci
\[\vec B = \mathrm{rot}\,\vec A=\nabla\times\vec A.\]Poznámka: V úloze používáme normalizaci \(\nabla\cdot \vec A = 0\).
Nápověda 3 – vhodná volba souřadné soustavy
Pro integraci využijte sférických souřadnic, přičemž postupujte následujícím způsobem:
Soustavu souřadnic zvolte tak, aby bod \(\vec r\), ve kterém počítáte potenciál, ležel na kladné poloose z. Dále tak, aby osa otáčení ležela v rovině xz. Úhel mezi osou z a osou otáčení označte ψ. Viz obrázek.
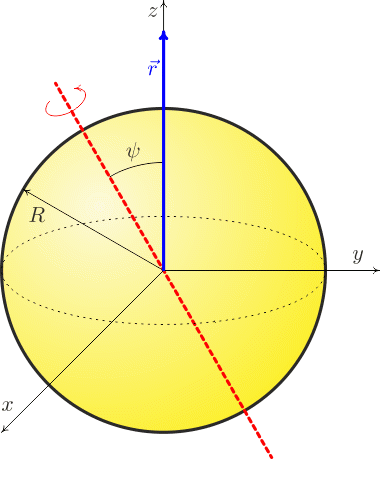
Integrujte přes plošky dS' na povrchu koule. Integrujte ve sférických souřadnicích přes úhly θ' (odklon místa plošky od osy z, v mezích od nuly do π) a φ' (odklon průmětu plošky do roviny xy od osy x, v mezích od nuly do 2π).
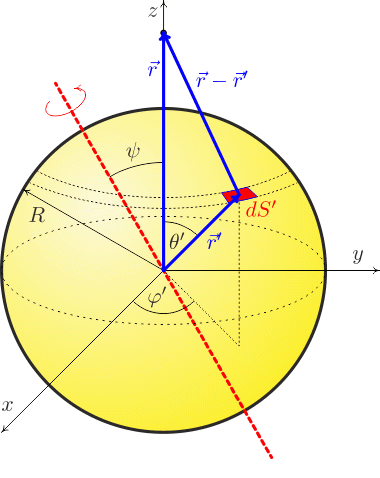
Vektor \(\vec r'\) začíná v počátku a končí v plošce dS' na ploše koule, má tedy délku R. Ploška dS' se nachází na pásku určeném úhlem θ', který obepíná sféru v ploše kolmé na osu z. Tento pásek má poloměr R sinθ' a tloušťku R dθ'.
Ploška dále leží na pásku v místě, určeném úhlem φ' a její délka podél pásku je určena malým úhlem dφ'. Tento úhel dφ' vytíná na pásku o poloměru R sinθ' úsečku o délce R sinθ' dφ'.
Odtud dostáváme, že dS' = R2 sinθ' dθ' dφ'.
Vyjádřete \(|\vec r-\vec r^,|\) s použitím kosinové věty pomocí r, R, θ'.
Vyjádřete vektorový součin v plošné hustotě proudu \(\vec k\) pomocí velikosti vektorů \(\vec\omega\) a \(\vec r^,\), úhlových sférických souřadnic θ', φ' a úhlu ψ, který svírá osa otáčení s osou z.
Nezapomeňte, že integrujete vektorovou funkci! Integrujte tedy jednotlivé složky zvlášť.
Uvědomte si, že integrál sinu či kosinu přes periodu 2π je nulový.
Řešení – sestavení integrálu

Počítejme potenciál v bodě \(\vec r\), který speciálně volme v ose z. Osa z ovšem v takovém případě nemusí být totožná s osou otáčení, viz předchozí nápovědu! Užijeme vztah
\[\vec A(\vec r) = \frac{\mu_0}{4\pi}\int \frac{\vec k(\vec r^,)}{|\vec r-\vec r^,|}\,dS^, ,\]kde pro plošnou hustotu proudu \(\vec k\) platí
\[\vec k = \sigma\vec v.\]Obvodová rychlost \(\vec v\) v bodě \(\vec r^,\) je dána vztahem
\[\vec v = \vec\omega \times\vec r^, .\]Podle kosinové věty platí
\[|\vec r-\vec r^,| = \sqrt{R^2+r^2-2Rr\cos\theta^{,}}\]a plošku dS' můžeme vyjádřit ve sférických souřadnicích jako
\[dS^, = R^2\sin\theta^,\mathrm{d}\theta^,\mathrm{d}\varphi^, .\]Integrujeme tedy přes plošky na sféře, které mají délku R sinθ' dφ' a tloušťku R dθ', přičemž φ' má meze od 0 do 2π (odpovídá opsání vodorovného kruhového řezu koulí) a θ' má meze od 0 do π (řezy cestují od horního do spodního okraje koule).
Poznámka: Ke vztahu pro dS lze dojít i formálními úvahami: integrujeme ve sférických souřadnicích, ve kterých platí, že dV = r2 sin θ dr dθ dφ a zároveň dS = dV/dr = r2 sin θ dθ dφ. Přitom, jsme-li na povrchu sféry, pak zřejmě r = R.
Po dosazení do vztahu
\[\vec A(\vec r) = \frac{\mu_0}{4\pi}\int \frac{\vec k(\vec r^,)}{|\vec r-\vec r^,|}\,\mathrm{d}S^,\]za veličiny \(\vec k\), \(|\vec r-\vec r^,|\) a \(dS^,\) vztahy uvedené výše dostaneme
\[\vec A(\vec r) = \frac{\mu_0}{4\pi}\int_\mathrm{povrch} \frac{\sigma(\omega\times\vec r^,)}{\sqrt{R^2+r^2-2Rr\cos\theta^,}}\,R^2\,\sin\theta^,\,\mathrm{d}\varphi^,\,\mathrm{d}\theta^,\]a (dvojný) integrál přes povrch koule můžeme napsat jako dvojici integrálů
\[\vec A(\vec r) = \frac{\mu_0}{4\pi}\int_0^\mathrm{\pi}\int_0^{2\pi} \frac{\sigma(\vec\omega\times\vec r^,)}{\sqrt{R^2+r^2-2Rr\cos\theta^,}}\,R^2\,\sin\theta^,\,\mathrm{d}\varphi^,\,\mathrm{d}\theta^, .\tag{+}\]Zbývá vyjádřit vektorový součin \(\vec\omega \times\vec r^,\) pomocí zadaných konstant (velikosti úhlové rychlosti ω, poloměru koule R, úhlu ψ) a souřadnic θ', φ'.
Řešení – výpočet složek vektorového potenciálu

Osa otáčení je vůči ose z sklopena v rovině y = 0 o (pevný) úhel ψ. Potom pro úhlovou rychlost platí
\[\vec\omega = (\omega\,\sin\psi,\, 0,\,\omega\,\cos\psi).\]Kartézské souřadnice vektoru \(\vec r^,\) můžeme pomocí sférických souřadnic vyjádřit jako
\[\vec r^, = (R\,\sin\,\theta^,\,\cos\,\varphi^,,\,R\,\sin\,\theta^,\,\sin\,\varphi^,,\,R\,\cos\,\theta^,).\]Vektorový součin pak má složky
\[(\vec\omega \times\vec r^,)_\mathrm{x} = R\omega\,(-\cos\,\psi\,\sin\,\theta^,\,\sin\,\varphi^,),\] \[(\vec\omega \times\vec r^,)_\mathrm{y} = R\omega\,(\cos\,\psi\,\sin\,\theta^,\,\cos\,\varphi^,-\sin\,\psi\,\cos\,\theta^,),\] \[(\vec\omega \times\vec r^,)_\mathrm{z} = R\omega\,(\sin\,\psi\,\sin\,\theta^,\,\sin\varphi^,).\]Pomocí tohoto vyjádření přepišme integrál (+) pro vektorový potenciál \(\vec A\) do složek:
\[A_\mathrm{x}(\vec r) = \frac{\mu_0}{4\pi}\int_0^{\pi}\int_0^{2\pi} \frac{\sigma\,R^3\omega (-\cos\,\psi\,\sin\,\theta^,\sin\,\varphi^,)}{\sqrt{R^2+r^2-2Rr\cos\theta^,}}\,\sin\theta^,\,\mathrm{d}\varphi^,\,\mathrm{d}\theta^, \] \[A_\mathrm{y}(\vec r) = \frac{\mu_0}{4\pi}\int_0^{\pi}\int_0^{2\pi} \frac{\sigma\,R^3\omega (\cos\psi\sin\theta^,\cos\,\varphi^,-\sin\psi\cos\theta^,)}{\sqrt{R^2+r^2-2Rr\cos\theta^,}}\sin\theta^,\mathrm{d}\varphi^,\mathrm{d}\theta^, \] \[A_\mathrm{z}(\vec r) = \frac{\mu_0}{4\pi}\int_0^{\pi}\int_0^{2\pi} \frac{\sigma\,R^3\omega (\sin\,\psi\,\sin\,\theta^,\,\sin\varphi^,)}{\sqrt{R^2+r^2-2Rr\cos\theta^,}}\,\sin\theta^,\,\mathrm{d}\varphi^,\,\mathrm{d}\theta^, ,\]a tyto integrály můžeme upravit do tvaru
\[A_x(\vec r) = \frac{\mu_0}{4\pi}\int_0^{2\pi}\sin\,\varphi^,\,\mathrm{d}\varphi^,\int_0^{\pi} \frac{\sigma\,R^3\omega (-\cos\,\psi\,\sin\,\theta^,)}{\sqrt{R^2+r^2-2Rr\cos\theta^,}}\,\sin\theta^,\,\mathrm{d}\theta^,\] \[A_y(\vec r) = \frac{\mu_0}{4\pi}\int_0^{2\pi}\cos\,\varphi^,\,\mathrm{d}\varphi^,\int_0^{\pi} \frac{\sigma\,R^3\omega (\cos\,\psi\,\sin\,\theta^,)}{\sqrt{R^2+r^2-2Rr\cos\theta^,}}\,\sin\theta^,\,\mathrm{d}\theta^, -\] \[- \frac{\mu_0}{4\pi}\int_0^{2\pi}\,\mathrm{d}\varphi^,\int_0^{\pi} \frac{\sigma\,R^3\omega (\sin\,\psi\,\cos\,\theta^,)}{\sqrt{R^2+r^2-2Rr\cos\theta^,}}\,\sin\theta^,\,\mathrm{d}\theta^, \] \[A_z(\vec r) = \frac{\mu_0}{4\pi}\int_0^{2\pi}\sin\,\varphi^,\,\mathrm{d}\varphi^,\int_0^{\pi} \frac{\sigma\,R^3\omega (\sin\,\psi\,\sin\,\theta^,)}{\sqrt{R^2+r^2-2Rr\cos\theta^,}}\,\sin\theta^,\,\,\mathrm{d}\theta^,.\]Protože platí
\[\int_0^{2\pi} \sin\varphi^,\,\mathrm{d}\varphi^, = \int_0^{2\pi} \cos\varphi^,\,\mathrm{d}\varphi^, = 0,\]zjednoduší se integrály na tvary
\[A_\mathrm{x}(\vec r) = 0,\] \[A_\mathrm{y}(\vec r) = - \frac{\mu_0}{4\pi}\int_0^{2\pi}\,d\varphi^,\int_0^{\pi} \frac{\sigma\,R^3\omega (\sin\,\psi\,\cos\,\theta^,)}{\sqrt{R^2+r^2-2Rr\cos\theta^,}}\,\sin\theta^,\,\mathrm{d}\theta^, \] \[A_\mathrm{z}(\vec r) = 0.\]Vidíme, že vektorový potenciál \(\vec A(\vec r)\) bude mít nenulovou pouze y-ovou složku a ta bude mít velikost
\[A_\mathrm{y}(\vec r) = -\frac{\mu_0}{4\pi}\int_0^{2\pi}\,\mathrm{d}\varphi^,\int_0^\pi \frac{\sigma\,R^3\omega\, \sin\psi\,\cos\theta^,}{\sqrt{R^2+r^2-2Rr\cos\theta^,}}\,\sin\theta^,\,\mathrm{d}\theta^, =\] \[= -\frac{\mu_0R^3\sigma\omega \sin\psi}{2}\int_0^\pi \frac{\sin\theta^,\cos\theta^,}{\sqrt{R^2+r^2-2Rr\cos\theta^,}}\,\mathrm{d}\theta^,=.\]Pro výpočet integrálu zkuste použít substituci u = cos θ'. Podrobný výpočet je uveden v komentáři na konci úlohy. Po provedení integrace vyjde
\[= \frac{\mu_0R^3\sigma\omega \sin\psi}{2}\frac{1}{3R^2r^2}\left[(R^2+r^2+Rr)|R-r|-(R^2+r^2-Rr)(R+r)\right].\tag{*}\]Rozvažme dva případy podle absolutní hodnoty ve výsledku.
(i) Pokud bod \(\vec r\) leží uvnitř koule, potom r < R a |R − r| = R − r, pak hranatá závorka ve vztahu (*) vyjde
\[\left[(R^2+r^2+Rr)|R-r|-(R^2+r^2-Rr)(R+r)\right] =\] \[=\left[(R^2+r^2+Rr)(R-r)-(R^2+r^2-Rr)(R+r)\right] = -2r^3\]a pro y-ovou složku vektorového potenciálu tudíž máme
\[A_\mathrm{y} = -\frac{\mu_0R\sigma}{3}(\omega r\sin\psi),\]kde výraz v závorce určuje velikost vektorového součinu \(|\vec\omega \times \vec r|\), takže můžeme psát
\[A_\mathrm{y} = -\frac{\mu_0R\sigma}{3}|\vec \omega\times\vec r|.\]Protože velikost vektorového součinu je kladné číslo, je složka Ay záporná, a tudíž vektor \(\vec A\) míří ve směru záporné poloosy y. (Připomeňme na tomto místě, že v tuto chvíli počítáme ve speciálně zvolené soustavě souřadnic.)
A protože vektor \(\vec\omega\times\vec r\) podle pravidla pravé ruky míří ve směru záporné poloosy y, můžeme psát
\[\vec A(\vec r) = \frac{\mu_0R\sigma}{3}(\vec \omega\times\vec r).\]Všimněte si, že poslední výraz neobsahuje složky žádného vektoru, a tudíž platí při libovolné volbě soustavy souřadnic.
(ii) Pokud bod \(\vec r\) leží vně koule, potom r > R a |R − r| = r − R, pak hranatá závorka ve vztahu (*) vyjde
\[\left[(R^2+r^2+Rr)|R-r|-(R^2+r^2-Rr)(R+r)\right] =\] \[=\left[(R^2+r^2+Rr)(r-R)-(R^2+r^2-Rr)(R+r)\right] = -2R^3\]a pro y-ovou složku vektorového potenciálu tak máme
\[A_\mathrm{y} = \frac{\mu_0R^4\sigma}{3r^3}(-\omega r\sin\psi) = \frac{\mu_0R^4\sigma}{3r^3}|\vec\omega\times\vec r|.\]Z obdobných úvah jako výše dostaneme, že
\[\vec A(\vec r) = \frac{\mu_0R^4\sigma}{3r^3}(\vec \omega\times\vec r).\]Vizualizace vektorového potenciálu
Nyní opustíme speciální soustavu souřadnic, kterou jsme zavedli kvůli výpočtu vektorového potenciálu, a vrátíme se k „přirozenější“ vztažné soustavě, ve které osa rotace bude mířit vzhůru, ve směru kladné poloosy z.
Vektorový potenciál uvnitř koule
Pro vektorový potenciál uvnitř koule jsme odvodili vztah
\[\vec A = \frac{\mu_0R\sigma}{3}(\vec\omega\times\vec r).\]Všimněme si nejprve, že pro jeho velikost platí
\[A = \frac{\mu_0R\sigma\omega}{3}r\sin\psi ,\]kde ve zlomku jsou konstanty a výraz r sinψ určuje vzdálenost od osy otáčení. S rostoucí vzdáleností od osy otáčení tedy velikost vektoru \(\vec A\) lineárně roste.
Co se týče směru, podle pravidla pravé ruky obíhá vektorový potenciál kolem osy otáčení (palec ukazuje vektor \(\vec\omega\), zahnuté prsty směr obíhání, zcela analogicky jako tomu je u pohybu po kružnici).
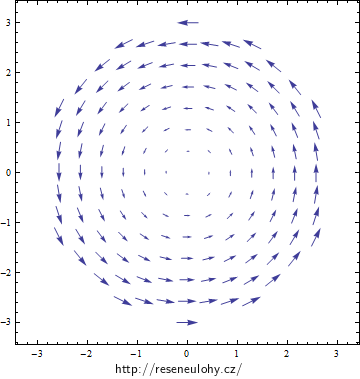
Pohled seshora podél osy otáčení na vektorový potenciál magnetického pole uvnitř rotující nabité koule.
Vektorový potenciál vně koule
Pro vektorový potenciál vně rotující nabité koule jsme odvodili vztah
\[\vec A = \frac{\mu_0R^4\sigma}{3r^3}(\vec\omega\times\vec r).\]Pro jeho velikost platí
\[A = \frac{\mu_0R^4\sigma\omega}{3}\ \frac{r\sin\psi}{r^3} ,\]kde v prvním zlomku jsou konstanty. Výraz r sinψ určuje vzdálenost od osy otáčení. S rostoucí vzdáleností od osy otáčení tedy velikost vektoru \(\vec A\) lineárně roste, ale zároveň klesá se třetí mocninou vzdálenosti od počátku. Pokud zafixujeme úhel ψ — tj. pevně si zvolíme přímku procházející počátkem, na které potenciál vyšetřujeme — pak na této přímce jeho velikost klesá s druhou mocninou vzdálenosti od počátku.
Poznámka: Podobně tomu je u potenciálu elektrického pole ideálního dipólu. Že tato podobnost není čistě náhodná, ještě uvidíme při výpočtu magnetické indukce níže.
Co se týče směru, je to stejné jako uvnitř koule. Podle pravidla pravé ruky obíhá vektorový potenciál kolem osy otáčení (palec ukazuje vektor \(\vec\omega\), zahnuté prsty směr obíhání, zcela analogicky jako tomu je u pohybu po kružnici).
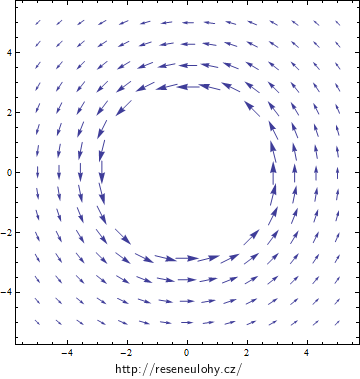
Pohled seshora podél osy otáčení na vektorový potenciál magnetického pole vně rotující nabité koule.
Komentář – výpočet integrálu
Vypočteme integrál
\[\int_0^\pi \frac{\sin\theta^,\,\cos\theta^,}{\sqrt{R^2+r^2-2Rr\,\cos\theta^,}}\,\mathrm{d}\theta^,.\]Použijeme substituci
\[u = \cos\theta^,\qquad \mathrm{d}u = -\sin\theta^,\,\mathrm{d}\theta^, ,\]pomocí níž integrál přejde na tvar
\[-\int_1^{-1} \frac{u}{\sqrt{R^2+r^2-2Rru}}\,\mathrm{d}u = \int_{-1}^{1} \frac{u}{\sqrt{R^2+r^2-2Rru}}\,\mathrm{d}u.\]Nyní použijeme druhou substituci
\[t = R^2+r^2-2Rru,\qquad \mathrm{d}t = -2Rr\,\mathrm{d}u,\]přičemž zřejmě zpětně platí, že
\[u = \frac{t-R^2-r^2}{-2Rr}, \qquad \mathrm{d}u = -\frac{\mathrm{d}t}{2Rr}.\]Touto substitucí integrál přejde na tvar
\[\frac{1}{4R^2r^2}\qquad\int_\mathrm{R^2+r^2+2Rr}^\mathrm{R^2+r^2-2Rr} \frac{t-R^2-r^2}{\sqrt{t}}\,\mathrm{d}t,\]odkud úpravou dostaneme
\[\frac{1}{4R^2r^2}\int_\mathrm{(R+r)^2}^\mathrm{(R-r)^2} \left(\sqrt{t}-\frac{R^2+r^2}{\sqrt{t}}\right)\,\mathrm{d}t = \frac{1}{4R^2r^2}\left[\frac{t^{3/2}}{3/2}-(R^2+r^2)\frac{t^{1/2}}{1/2}\right]_\mathrm{(R+r)^2}^\mathrm{(R-r)^2} =\] \[= \frac{1}{4R^2r^2}\left[\frac{2}{3}\sqrt t\left(t-3R^2-3r^2\right)\right]_\mathrm{(R+r)^2}^\mathrm{(R-r)^2}\ .\]Odkud po dosazení horní a dolní meze dostaneme
\[= \frac{1}{4R^2r^2}\left[\frac{2}{3}|R-r|\left(-2R^2-2r^2-2Rr\right)-\frac{2}{3}(R+r)\left(-2R^2-2r^2+2Rr\right)\right] =\] \[= -\frac{1}{3R^2r^2}\left[|R-r|\left(R^2+r^2+Rr\right)- (R+r)\left(R^2+r^2-Rr\right)\right].\]Řešení – výpočet magnetické indukce uvnitř koule
Magnetickou indukci dostaneme provedením operátoru rotace na vektorový potenciál \(\vec A\). Uvnitř koule platí
\[\vec B = \nabla\times\vec A = \frac{\mu_0R\sigma}{3}\left[\nabla\times(\vec\omega\times\vec r)\right].\]Výpočet si zjednodušíme, pokud volíme speciální soustavu souřadnic, v níž vektor úhlové rychlosti míří ve směru kladné poloosy z a má tedy složky \(\vec\omega = (0,\,0,\,\omega)\). Potom
\[\vec\omega\times\vec r = (-\omega y,\,\omega x,\,0)\]a rotace tohoto vektoru je rovna
\[\nabla\times (\vec\omega\times\vec r) = \left(0-\frac{\partial}{\partial z}(\omega x), \,\frac{\partial}{\partial z}(-\omega y)-0,\,\frac{\partial}{\partial x}(\omega x)-\frac{\partial}{\partial y}(-\omega y)\right) = (0,\,0,\,2\omega).\]Odtud vyplývá, že vektor \(\nabla\times(\vec\omega\times\vec r)\) je orientován do kladné poloosy z, tedy stejně jako vektor \(\vec\omega\), a má velikost 2ω. Proto
\[\nabla\times (\vec\omega\times\vec r) = 2\vec\omega\]a dosazením do vztahu pro magnetickou indukci dostáváme
\[\vec B = \nabla\times\vec A = \frac{2}{3}\mu_0R\sigma\vec\omega.\]Z výsledného vztahu je vidět, že jde o homogenní magnetické pole mířící ve směru osy otáčení.
Poznámka: Při výpočtu lze také použít vektorové identity (platné pro libovolné vektory \(\vec\omega\) a \(\vec r\)):
\[\nabla\times(\vec\omega\times\vec r) = (\vec r\cdot\nabla)\vec\omega - (\vec\omega\cdot\nabla)\vec r + \vec\omega(\nabla\cdot\vec r)-\vec r(\nabla\cdot\vec\omega).\tag{I}\]První a poslední člen jsou nulové, neboť \(\vec\omega\) je konstantní vektor. Dále platí, že
\[\nabla\cdot\vec r = \frac{\partial}{\partial x}(x) + \frac{\partial}{\partial y}(y) + \frac{\partial}{\partial z}(z) = 1+1+1 = 3,\]a tudíž
\[\vec\omega(\nabla\cdot\vec r) = 3\omega.\]Pišme
\[\vec\omega = (\omega_\mathrm{x},\omega_\mathrm{y},\omega_\mathrm{z}).\]Potom \((\vec\omega\cdot\nabla)\) je operátor:
\[(\vec\omega\cdot\nabla) = \left(\omega_\mathrm{x}\frac{\partial}{\partial x}+\omega_\mathrm{y}\frac{\partial}{\partial y}+\omega_\mathrm{z}\frac{\partial}{\partial z}\right),\]který působí jednotlivě na každou složku vektoru \(\vec r\). Tudíž výsledkem je vektor o složkách
\[[(\vec\omega\cdot\nabla)\vec r]_\mathrm{x} = (\vec\omega\cdot\nabla)(x) = \left(\omega_\mathrm{x}\frac{\partial}{\partial x}+\omega_\mathrm{y}\frac{\partial}{\partial y}+\omega_\mathrm{z}\frac{\partial}{\partial z}\right)(x)=\] \[= \omega_\mathrm{x}\frac{\partial}{\partial x}(x)+\omega_\mathrm{y}\frac{\partial}{\partial y}(x)+\omega_\mathrm{z}\frac{\partial}{\partial z}(x) = \omega_\mathrm{x} + 0 + 0 = \omega_\mathrm{x}.\]Podobně dostaneme, že
\[[(\vec\omega\cdot\nabla)\vec r]_\mathrm{y} = \omega_\mathrm{y},\] \[[(\vec\omega\cdot\nabla)\vec r]_\mathrm{z} = \omega_\mathrm{z},\]a tedy
\[(\vec\omega\cdot\nabla)\vec r = (\omega_\mathrm{x},\,\omega_\mathrm{y},\,\omega_\mathrm{z}) = \vec\omega.\]Dosazením do identity (I) dostaneme, že
\[\nabla\times(\vec\omega\times\vec r) = 0 - \vec\omega + 3\vec\omega - 0 = 2\vec\omega.\]Řešení – výpočet magnetické indukce vně koule
Magnetickou indukci dostaneme provedením operátoru rotace na vektorový potenciál \(\vec A\). Vně koule platí
\[\vec B = \nabla\times\vec A = \frac{\mu_0R^4\sigma}{3}\left[\nabla\times\left(\vec\omega\times\frac{\vec r}{r^3}\right)\right].\tag{B1}\]Pro výpočet užijeme identity, platné pro libovolné vektory \(\vec a\) a \(\vec b\):
\[\nabla\times(\vec a\times\vec b) = (\vec b\cdot\nabla)\vec a - (\vec a\cdot\nabla)\vec b + (\nabla\cdot\vec b)\vec a - (\nabla\cdot\vec a)\vec b.\]Pokud v identitě píšeme \(\vec\omega\) namísto \(\vec a\) a \(\vec{r}/r^3\) namísto \(\vec b\), dostáváme
\[\nabla\times\left(\vec\omega\times \frac{\vec r}{r^3}\right)=\left(\frac{\vec r}{r^3}\cdot\nabla\right)\vec\omega- (\vec\omega\cdot\nabla)\frac{\vec r}{r^3} + \left(\nabla\cdot\frac{\vec r}{r^3}\right)\vec\omega - \left(\nabla\cdot\vec \omega\right)\frac{\vec r}{r^3}.\tag{B2}\]První a čtvrtý člen jsou nulové, neboť v obou z nich působí diferenciální operátor na konstantní vektor \(\vec{\omega}\).
Také třetí člen je (vně koule) nulový, neboť
\[\nabla\cdot\frac{\vec r}{r^3} = 0.\]Máme totiž (ve všech bodech kromě počátku)
\[\nabla\cdot\frac{\vec r}{r^3} = \frac{\partial}{\partial x}\left(\frac{x}{r^3}\right) + \frac{\partial}{\partial x}\left(\frac{y}{r^3}\right) + \frac{\partial}{\partial x}\left(\frac{z}{r^3}\right) = \frac{\partial}{\partial x}\left(\frac{x}{(x^2+y^2+z^2)^{3/2}}\right) +\] \[+ \frac{\partial}{\partial x}\left(\frac{y}{(x^2+y^2+z^2)^{3/2}}\right) + \frac{\partial}{\partial x}\left(\frac{z}{(x^2+y^2+z^2)^{3/2}}\right) = \frac{(x^2+y^2+z^2)^{3/2}-x\,\frac{3}{2}(x^2+y^2+z^2)^{1/2}\,2x}{(x^2+y^2+z^2)^{3}} +\] \[+ \frac{(x^2+y^2+z^2)^{3/2}-y\,\frac{3}{2}(x^2+y^2+z^2)^{1/2}\,2y}{(x^2+y^2+z^2)^{3}} + \frac{(x^2+y^2+z^2)^{3/2}-z\,\frac{3}{2}(x^2+y^2+z^2)^{1/2}\,2z}{(x^2+y^2+z^2)^{3}} =\] \[=\frac{3(x^2+y^2+z^2)^{3/2}-3(x^2+y^2+z^2)(x^2+y^2+z^2)^{1/2}}{(x^2+y^2+z^2)^3} = 0.\]Pro úplnost poznamenejme, že výsledek platí ve všech bodech s výjimkou počátku soustavy souřadnic, nás ale zajímají pouze body vně koule.
Zbývá tedy spočítat poslední člen
\[\left(\vec\omega\cdot\nabla\right)\frac{\vec r}{r^3}.\]Označme \(\vec\omega = (\omega_\mathrm{x},\,\omega_\mathrm{y},\,\omega_\mathrm{z})\). V závorce je diferenciální operátor
\[\left(\vec\omega\cdot\nabla\right) = \left(\omega_\mathrm{x}\frac{\partial}{\partial x} + \omega_\mathrm{y}\frac{\partial}{\partial y} + \omega_\mathrm{z}\frac{\partial}{\partial z}\right),\]který působí na každou složku vektoru \(\vec r/r^3 = (x/r^3,\,y/r^3,\,z/r^3)\). Výsledkem je tedy vektor, pro jehož
x-ovou složku platí
\[\left[(\nabla\cdot\vec\omega)\frac{\vec r}{r^3}\right]_\mathrm{x} = \left[\omega_\mathrm{x}\frac{\partial}{\partial x} + \omega_\mathrm{y}\frac{\partial}{\partial y} + \omega_\mathrm{z}\frac{\partial}{\partial z}\right]\left(\frac{x}{r^3}\right) = \left[\omega_\mathrm{x}\frac{\partial}{\partial x} + \omega_\mathrm{y}\frac{\partial}{\partial y} + \omega_\mathrm{z}\frac{\partial}{\partial z}\right]\left(\frac{x}{(x^2+y^2+z^2)^{3/2}}\right).\tag{1}\]Platí, že
\[\frac{\partial}{\partial x}\left(\frac{x}{(x^2+y^2+z^2)^{3/2}}\right) = \] \[=\frac{(x^2+y^2+z^2)^{3/2} - 3x^2(x^2+y^2+z^2)^{1/2}}{(x^2+y^2+z^2)^3} =\frac{(x^2+y^2+z^2) - 3x^2}{(x^2+y^2+z^2)^{5/2}} = \frac{r^2-3x^2}{r^5}.\tag{2}\]Dále máme
\[\frac{\partial}{\partial y}\left(\frac{x}{(x^2+y^2+z^2)^{3/2}}\right) = \frac{0 - 3xy(x^2+y^2+z^2)^{1/2}}{(x^2+y^2+z^2)^3}=\frac{-3xy}{(x^2+y^2+z^2)^{5/2}} = -\frac{3xy}{r^5},\tag{3}\]podobně
\[\frac{\partial}{\partial z}\left(\frac{x}{(x^2+y^2+z^2)^{3/2}}\right) = \frac{0 - 3xy(x^2+y^2+z^2)^{1/2}}{(x^2+y^2+z^2)^3} =\frac{-3xz}{(x^2+y^2+z^2)^{5/2}} = -\frac{3xz}{r^5}.\tag{4}\]Dosazením vztahů (2)-(4) do (1) dostaneme, že
\[\left[(\nabla\cdot\vec\omega)\frac{\vec r}{r^3}\right]_\mathrm{x} = \frac{\omega_\mathrm{x}(r^2-3x^2)+\omega_\mathrm{y}(-3xy)+\omega_\mathrm{z}(-3xz)}{r^5}= \frac{\omega_\mathrm{x}}{r^3} - \frac{3x}{r^5}(\omega_\mathrm{x}x+\omega_\mathrm{y}y+\omega_\mathrm{z}z) = \frac{\omega_\mathrm{x}}{r^3} - \frac{3x}{r^5}(\vec\omega\cdot\vec r).\]Navlas stejným postupem (nebo cyklickou záměnou souřadnic) zjistíme, že platí
\[\left[(\nabla\cdot\vec\omega)\frac{\vec r}{r^3}\right]_\mathrm{y} = \frac{\omega_\mathrm{y}}{r^3} - \frac{3y}{r^5}(\vec\omega\cdot\vec r),\] \[\left[(\nabla\cdot\vec\omega)\frac{\vec r}{r^3}\right]_\mathrm{z} = \frac{\omega_z}{r^3} - \frac{3z}{r^5}(\vec\omega\cdot\vec r).\]Vektorově lze výsledek psát ve tvaru
\[\left[(\nabla\cdot\vec\omega)\frac{\vec r}{r^3}\right] = \frac{1}{r^5}\left(r^2\vec\omega - 3(\vec\omega\cdot\vec r)\vec r\right).\]Pro magnetickou indukci vně rotující koule postupným dosazením posledního vztahu do (B2) a (B1) dostaneme
\[\vec B = \frac{\mu_0R^4\sigma}{3r^5}\left(3(\vec\omega\cdot\vec r)\vec r - r^2\vec\omega\right).\]Poznámka: Pro magnetickou indukci pole magnetického dipólu s magnetickým (dipólovým) momentem \(\vec m\) platí
\[\vec B_\mathrm{dip}(\vec r) = \frac{\mu_0}{4\pi r^5}\left(3(\vec m\cdot\vec r)\vec r - r^2\vec m\right).\]Porovnáním tohoto vztahu s předchozím zjistíme, že vně rotující nabité koule má pole stejný charakter jako pole magnetického dipólu s magnetickým momentem:
\[\vec m = \frac{4}{3}\pi R^4\sigma\vec\omega = V\sigma R\vec\omega.\]Na tento výsledek se odvoláváme v úloze Magnetické pole homogenně zmagnetované koule.
Odpověď
Magnetický vektorový potenciál uvnitř koule je dán vztahem
\[\vec A(\vec r) = \frac{\mu_0R\sigma}{3}(\vec\omega\times\vec r)\]a vně koule platí
\[\vec A(\vec r) = \frac{\mu_0R^4\sigma}{3r^3}(\vec\omega\times\vec r).\]Magnetické pole uvnitř koule je homogenní, pro magnetickou indukci platí
\[\vec B(\vec r) = \nabla\times\vec A(\vec r) = \frac{2}{3}\mu_0\sigma R\vec\omega.\]Magnetické pole vně koule je stejné jako pole magnetického dipólu s magnetickým momentem
\[\vec m = \frac{4}{3}\pi R^4\sigma\vec\omega,\]pro magnetickou indukci platí
\[\vec B(\vec r) = \nabla\times\vec A(\vec r) = \frac{\mu_0R^4\sigma}{3r^5}\left(3(\vec\omega\cdot\vec r)\vec r - r^2\vec\omega\right).\]Poznámka: Používáme normalizaci \(\nabla\cdot\vec A = 0\).

