Celková admitance v obvodu
Úloha číslo: 606
Vypočítejte admitanci a efektivní hodnotu proudu v obvodu, který je tvořen paralelním zapojením reálné cívky s indukčností 254 mH a odporem 60 Ω, rezistoru o odporu 50 Ω a ideálního kondenzátoru s kapacitou 127 μF. Střídavé napětí zdroje má efektivní hodnotu 100 V a frekvence napětí je 50 Hz.
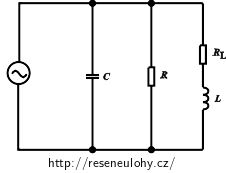
Zápis
RL = 60 Ω odpor cívky L = 254 mH indukčnost cívky R = 50 Ω odpor rezistoru C = 127 μF kapacita kondenzátoru U = 100 V efektivní hodnota napětí f = 50 Hz frekvence napětí zdroje Y = ? (S) celková admitance obvodu I = ? (A) efektivní hodnota proudu Nápověda – co je to admitance
Admitance Y obvodu vyjadřuje zdánlivou vodivost obvodu a fázový posun mezi napětím a proudem při průběhu harmonického střídavého napětí. Získáme ji jako převrácenou hodnotu impedance Z obvodu.
Jednotkou admitance je stejně jako u vodivosti v případě stejnosměrného proudu siemens (značíme S, [Y] = S).
Admitanci zavádíme pro snazší výpočty u paralelních obvodů. Protože zatímco v sériových obvodech získáme celkovou impedanci jako součet impedancí dílčích (jedná se o vektorový součet), tak naopak v paralelních obvodech získáme celkovou admitanci jako součet dílčích admitancí (opět vektorový součet) a Ohmův zákon potom nabývá tvaru:
\[ I = U Y .\]Rozbor
Jelikož je obvod paralelní, tak celkovou admitanci obvodu získáme jako součet dílčích admitancí reálné cívky, rezistoru a kondenzátoru.
Efektivní hodnotu proudu získáme pomocí Ohmova zákona pro střídavý proud, ve kterém vystupuje admitance.
Řešení pomocí komplexní symboliky
Pozn.: Komplexní jednotku budeme označovat j. Komplexní veličiny budeme značit pruhem.
Celkovou admitanci Y obvodu získáme jako součet admitancí jednotlivých větví, které lze vyjádřit jako převrácené hodnoty jejich impedancí.
1) Admitance reálné cívky \(\bar{Y}_\mathrm{L}\):
Pro impedanci cívky \(\bar{Z}_\mathrm{L} \) platí:
\[ \bar{Z}_\mathrm{L} = R_\mathrm{L} + X_\mathrm{L}\mathrm{j} = R_\mathrm{L} + \omega L\, \mathrm{j}= R_\mathrm{L} + 2 \pi f L\, \mathrm{j},\]kde RL je odpor cívky, XL induktance cívky a ω úhlová frekvence napětí v obvodu. Admitanci cívky \(\bar{Y}_\mathrm{L}\) získáme jako převrácenou hodnotu její impedance \(\bar{Z}_\mathrm{L} \):
\[ \bar{Y}_\mathrm{L} = \frac{1}{\bar{Z}_\mathrm{L}} = \frac{1}{R_\mathrm{L} + 2 \pi f L\,\mathrm{j}} =\] \[=\frac{1}{R_\mathrm{L} + 2 \pi f L\, \mathrm{j}}\ \frac{ R_\mathrm{L} - 2 \pi f L\, \mathrm{j}}{R_\mathrm{L} - 2 \pi f L \,\mathrm{j}} = \frac{ R_\mathrm{L} - 2 \pi f L\, \mathrm{j}}{R_\mathrm{L}^2 + (2 \pi f L)^2}=\frac{ R_\mathrm{L} }{R_\mathrm{L}^2 + (2 \pi f L)^2 }- \frac{2 \pi f L}{R_\mathrm{L}^2 + (2 \pi f L)^2} \mathrm{j}.\]2) Pro impedanci rezistoru \( \bar{Z}_\mathrm{R} \) platí:
\[ \bar{Z}_\mathrm{R} = R, \]kde R je jeho odpor. Admitanci rezistoru \( \bar{Y}_\mathrm{R} \) získáme jako převrácenou hodnotu jeho impedance \( \bar{Z}_\mathrm{R} \):
\[ \bar{Y}_\mathrm{R} = \frac{1}{\bar{Z}_\mathrm{R}} =\frac{1}{R}.\]3) Impedance kondenzátoru \( \bar{Z}_\mathrm{C} \) se rovná jeho kapacitanci XC, pro kterou platí:
\[ \bar{Z}_\mathrm{C} =- X_\mathrm{C} \mathrm{j} = - \frac{\mathrm{j}}{\omega C}= - \frac{\mathrm{j}}{2 \pi f C},\]kde ω je úhlová frekvence. Admitanci kondenzátoru \( \bar{Y}_\mathrm{C} \) získáme také jako převrácenou hodnotu jeho impedance \( \bar{Z}_\mathrm{C} \):
\[ \bar{Y}_\mathrm{C} = \frac{1}{\bar{Z}_\mathrm{C}} = \frac{1}{- \frac{\mathrm{j}}{2 \pi f C} } = 2 \pi f C\, \mathrm{j}. \]Celkovou admitanci \(\bar{Y}\) získáme jako součet admitancí jednotlivých větví:
\[\bar{Y} = \bar{Y}_\mathrm{L} + \bar{Y}_\mathrm{R} + \bar{Y}_\mathrm{C} =\] \[= \frac{ R_\mathrm{L} }{R_\mathrm{L}^2 + (2 \pi f L)^2 }- \frac{2 \pi f L}{R_\mathrm{L}^2 + (2 \pi f L)^2} \mathrm{j} + \frac{1}{R} + 2 \pi f C\, \mathrm{j}=\] \[= (\frac{ R_\mathrm{L} }{R_\mathrm{L}^2 + (2 \pi f L)^2}+ \frac{1}{R}) +(2 \pi f C-\frac{2 \pi f L }{R_\mathrm{L}^2 + (2 \pi f L)^2} )\,\mathrm{j}.\]Velikost celkové admitance Y určíme jako absolutní hodnotu komplexní admitance:
\[Y = |\bar{Y}|= | (\frac{ R_\mathrm{L} }{R_\mathrm{L}^2 + (2 \pi f L)^2}+ \frac{1}{R}) +(2 \pi f C-\frac{2 \pi f L }{R_\mathrm{L}^2 + (2 \pi f L)^2} )\,\mathrm{j}|= \] \[ = \sqrt{ ( \frac{1}{R}+\frac{ R_\mathrm{L} }{R_\mathrm{L}^2 + (2 \pi f L)^2})^2 +(2 \pi f C-\frac{2 \pi f L }{R_\mathrm{L}^2 + (2 \pi f L)^2} )^2}. \]Dosadíme číselně do vztahu pro admitanci Y:
\[Y = \sqrt{ (\frac{ R_\mathrm{L} }{R_\mathrm{L}^2 + (2 \pi f L)^2}+ \frac{1}{R})^2 +(2 \pi f C-\frac{2 \pi f L }{R_\mathrm{L}^2 + (2 \pi f L)^2} )^2}= \] \[=\sqrt{( \frac{ 60 }{60^2 + (2\cdot \pi \cdot 50 {\cdot} 254 \cdot 10^{-3})^2} + \frac{1}{50})^2 + ( 2 \cdot\pi \cdot 50 {\cdot} 127 \cdot 10^{-6} - \frac{2 \cdot \pi \cdot 50 {\cdot} 254 \cdot 10^{-3} }{60^2 + (2\cdot \pi \cdot 50 {\cdot} 254 \cdot 10^{-3})^2})^2} \,\mathrm S \,\dot=\] \[\dot= \,\sqrt{(\frac{ 60 }{60^2 + 80^2} + 0{,}02 )^2 + ( 0{,}04-\frac{ 80 }{60^2 + 80^2})^2}\,\mathrm S = \sqrt{0{,}026^2 + 0{,}032^2}\,\mathrm S \,\dot=\, 41{\cdot} 10^{-3} \,\mathrm S= 41\,\mathrm{mS}.\]
Efektivní hodnotu proudu I v obvodu určíme pomocí Ohmova zákona pro střídavý proud. Použijeme variantu, ve které vystupují efektivní hodnoty napětí U a proudu I a velikost celkové impedance Z, resp. admitance Y:
\[ I = \frac{U}{Z} = U Y. \]Dosadíme za admitanci:
\[ I = U Y = U\,|\bar{Y}| \,\dot{=}\, 100 {\cdot} 41\cdot 10^{-3} \,\mathrm A = 4{,}1\,\mathrm A. \]Řešení pomocí fázorů
Protože se jedná o paralelní obvod, celkovou admitanci Y obvodu získáme jako fázorový součet admitancí jednotlivých větví obvodu, tj. reálné cívky, rezistoru a kondenzátoru. Vše si znázorníme pomocí diagramu pro admitance, ve kterém zohledníme také fázový posun mezi napětím a proudem na jednotlivých součástkách.
a) Admitance reálné cívky YL:
Admitanci reálné cívky YL získáme jako převrácenou hodnotu její impedance ZL.
Impedanci reálné cívky ZL získáme z diagramu pro sériové zapojení induktance cívky XL a odporu cívky RL.
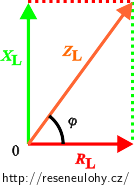
Impedanci reálné cívky ZL vyjádříme z diagramu a dosadíme číselné hodnoty:
\[ Z_\mathrm{L} = \sqrt{ R_\mathrm{L}^2 + X_\mathrm{L}^2 }= \sqrt{ R_\mathrm{L}^2 + (\omega L)^2 }= \sqrt{ R_\mathrm{L}^2 + (2 \pi f L)^2 }= \] \[ = \sqrt{60^2 + (2\cdot \pi \cdot 50 {\cdot} 254 \cdot 10^{-3})^2 }\,\mathrm \Omega\dot= \sqrt {60^2 + 80^2}= 100\,\mathrm \Omega. \]Admitanci reálné cívky YL dostaneme jako převrácenou hodnotu impedance ZL:
\[ Y_\mathrm{L} = \frac{1}{Z_\mathrm{L}} = \frac{1}{100} \,\mathrm S = 0{,}01 \,\mathrm S. \]Fázový posun φ mezi napětím a proudem vyjádříme ze stejného diagramu jako celkovou impedanci:
\[ \mathrm{tg}\,\varphi = \frac{X_\mathrm{L}}{R_\mathrm{L}}=\frac{\omega L}{R_\mathrm{L}}=\frac{2 \pi f L}{R_\mathrm{L}}=\frac{2\cdot \pi \cdot 50 {\cdot} 254 \cdot 10^{-3}}{60}\,\dot=\, \frac{80}{60}\,\dot=\,1{,}3 \qquad \Rightarrow \qquad \varphi = 53 ^\circ. \]Také si uvědomíme, že na cívce předbíhá napětí proud.
b) Admitance rezistoru YR:
Admitanci rezistoru YR získáme jako převrácenou hodnotu odporu rezistoru R:
\[ Y_\mathrm{R} = \frac{1}{R} = \frac{1}{50}\,\mathrm S = 0{,}02 \,\mathrm S. \]Na rezistoru je napětí a proud ve fázi.
c) Admitance kondenzátoru YC:
Admitanci kondenzátoru YC získáme jako převrácenou hodnotu impedance, resp. kapacitance kondenzátoru XC:
\[ Y_\mathrm{C} = \frac{1}{X_\mathrm{C}} = \frac{1}{\frac{1}{\omega C}}= \frac{1}{\frac{1}{2 \pi f C}}=2 \pi f C= 2 \cdot \pi \cdot 50 {\cdot} 127\cdot 10^{-6}\,\mathrm S \,\dot=\, 0{,}04 \,\mathrm S. \]Na kondenzátoru předbíhá proud napětí.
Celkovou admitanci Y získáme z fázorového diagramu. Protože se jedná o paralelní zapojení, je napětí na všech součástkách připojených v obvodu stejné, ale proudy se liší a mohou být vůči sobě i fázově posunuty. Proto je v následujícím diagramu zakresleno jediné napětí, ale tři různé proudy danými větvemi zapojení.
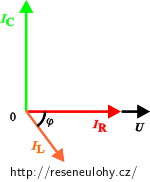
Pozn.: Velikosti fázorů v tomto i v následujících diagramech nejsou z důvodu názornosti obrázků v poměru k zadaným hodnotám.
Protože podle Ohmova zákona platí
\[ I = \frac{U}{Z}= \frac{U}{\frac{1}{Y}}= U Y \]a pro paralelní obvod je napětí na všech součástkách stejné, můžeme si fázorový diagram překreslit na diagram pro admitance:
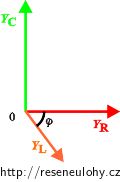
Celkovou admitanci obvodu získáme součtem všech tří admitancí, proto si nejprve rozložíme admitanci cívky YL do svislého a vodorovného směru:
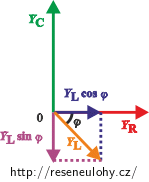
Pozn.: Tento krok není nutný, ale ulehčí nám výpočet, protože nebude třeba použít ko/sinovou větu, ale vystačíme si s jednodušší větou Pythagorovou.
Nyní budeme admitance sčítat jako vektory:
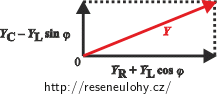
Vyjádříme z diagramu celkovou admitanci Y:
\[ Y = \sqrt{ (Y_\mathrm{R} + Y_\mathrm{L}\,\cos\,\varphi)^2 + (Y_\mathrm{C} - Y_\mathrm{L}\,\sin\,\varphi)^2 } .\]Dosadíme číselné hodnoty admitancí a vypočteme:
\[ Y = \sqrt{ (0{,}02 + 0{,}01 \cdot \cos\,53^\circ )^2 + (0{,}04 - 0{,}01\cdot \sin\,53^\circ)^2 }\,\mathrm S = 0{,}041\,\mathrm S = 41{\cdot} 10^{-3}\,\mathrm S=41\,\mathrm{mS} .\]
Efektivní hodnotu proudu I v obvodu určíme pomocí Ohmova zákona pro střídavý proud, ve kterém vystupuje celková admitance obvodu Y:
\[ I = \frac{U}{Z}= \frac{U}{\frac{1}{Y}}= U Y, \]kde U je efektivní hodnota napětí. Dosadíme číselně:
\[ I = 100 {\cdot} 0{,}041 \,\mathrm A = 4{,}1\,\mathrm A. \]Odpověď
Celková admitance obvodu má hodnotu přibližně 41 mS a efektivní hodnota proudu je asi 4,1 A.
Porovnání výsledků získaných pomocí řešení s komplexní symbolikou a řešení pomocí diagramu pro admitance
Celková impedance odvozená pomocí komplexní symboliky:
\[Y_\mathrm{K} = \sqrt{ ( \frac{1}{R}+\frac{ R_\mathrm{L} }{R_\mathrm{L}^2 + (2 \pi f L)^2})^2 +(2 \pi f C-\frac{2 \pi f L }{R_\mathrm{L}^2 + (2 \pi f L)^2} )^2}. \]Celková impedance odvozená pomocí diagramu pro admitance:
\[ Y_\mathrm{F} = \sqrt{ (\frac{1}{R} + Y_\mathrm{L}\cos{\varphi})^2 + (2 \pi f C- Y_\mathrm{L}\sin{\varphi})^2 } .\]
Při porovnání výše uvedených vztahů dojdeme k závěru, že pokud mají být vztahy rovnocenné, je třeba dokázat, že platí
\[ \frac{ R_\mathrm{L} }{R_\mathrm{L}^2 + (2 \pi f L)^2} = Y_\mathrm{L}\cos{\varphi},\] \[ \frac{2 \pi f L }{R_\mathrm{L}^2 + (2 \pi f L)^2}= Y_\mathrm{L}\sin{\varphi}.\]

Nejprve dokážeme, že
\[ \frac{ R_\mathrm{L} }{R_\mathrm{L}^2 + (2 \pi f L)^2} = Y_\mathrm{L}\cos{\varphi}.\]Z diagramu pro admitance platí:
\[ \sin{\varphi} = \frac{X_\mathrm{L}}{Z_\mathrm{L}}, \] \[ \cos{\varphi} = \frac{R_\mathrm{L}}{Z_\mathrm{L}}. \]Admitanci cívky YL lze vyjádřit ve tvaru
\[ Y_\mathrm{L} = \frac{1}{Z_\mathrm{L}} = \frac{1}{\sqrt{R_\mathrm{L}^2+X_\mathrm{L}^2}}.\]Nyní dosadíme do výrazu s kosinem:
\[ Y_\mathrm{L}\cos{\varphi} = \frac{1}{Z_\mathrm{L}}\cos{\varphi}=\frac{R_\mathrm{L}}{Z_\mathrm{L}^2}=\frac{R_\mathrm{L}}{R_\mathrm{L}^2+X_\mathrm{L}^2}=\frac{R_\mathrm{L}}{R_\mathrm{L}^2+(2\pi f L)^2}\]a vidíme, že jsme dokázali požadovanou rovnost.
Nyní dokážeme druhou rovnost:
\[ \frac{2 \pi f L }{R_\mathrm{L}^2 + (2 \pi f L)^2}= Y_\mathrm{L}\sin{\varphi}.\]Potřebné vztahy máme již vyjádené výše, dosadíme je do výrazu se sinem:
\[Y_\mathrm{L}\sin{\varphi} = \frac{1}{Z_\mathrm{L}}\sin{\varphi}=\frac{X_\mathrm{L}}{Z_\mathrm{L}^2}=\frac{X_\mathrm{L}}{R_\mathrm{L}^2+X_\mathrm{L}^2}=\frac{2 \pi f L}{R_\mathrm{L}^2+(2\pi f L)^2}\]a opět dostáváme hledanou rovnost.
Závěr: Dokázali jsme, že řešení pomocí komplexní symboliky a řešení pomocí diagramů pro admitance jsou stejná.

