Hliníkový kotouč v proměnném magnetickém poli
Úloha číslo: 791
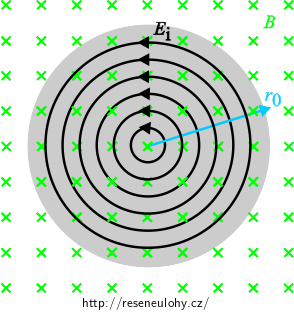
Hliníkový kotouč o poloměru 40 mm a tloušťce 1 mm vložíme do proměnného magnetického pole, jehož indukční čáry jsou kolmé k rovině kotouče. Závislost magnetické indukce na čase určuje vztah B = Bm cos (ωt), kde amplituda magnetické indukce Bm je 30 mT a úhlová frekvence ω = 100π rad/s.
Určete amplitudu proudu indukovaného v kotouči a amplitudu jeho výkonu.
Pozn.: Průřez hliníkového kotouče má obdélníkový tvar.
Nápověda 1
Uvědomte si, jak bude kotouč reagovat na proměnné magnetické pole, do kterého je vložen.
Nápověda 2
Kotouč můžeme rozdělit na malé prstence. V každém prstenci určíme velikost indukovaného elektrického pole, pomocí kterého určíme velikost indukovaného proudu v tom daném prstenci. Celkový indukovaný proud protékající kotoučem získáme jako součet proudů v jednotlivých prstencích.
Nápověda 3
Podle Ohmova zákona v diferenciálním tvaru je proudová hustota úměrná intenzitě elektrického pole. Elektrické pole v kotouči vzniká elektromagnetickou indukcí, tedy intenzitu indukovaného elektrického pole, resp. indukované napětí odvodíme pomocí Faradayova zákona elektromagnetické indukce.
Rozbor
Velikost amplitudy proudu indukovaného v kotouči odvodíme z časového průběhu indukovaného proudu. Pro odvození rovnice časového průběhu proudu je třeba kotouč rozdělit na elementární prstence a celkový indukovaný proud poté získáme pomocí integrace proudové hustoty přes celou plochu kotouče.
Amplitudu výkonu tohoto proudu odvodíme pomocí celkového výkonu, který získáme integrací jednotlivých elementů výkonu, které připadají na jednotlivé části prstence.
Řešení – maximální hodnota proudu
Celkový indukovaný proud I v kotouči získáme integrací hustoty elektrického proudu j přes plochu, kterou proud prochází:
\[ I = \int_\mathrm{S} j \mathrm{d}S, \]kde dS je element plochy obdélníku (poloviny průřezu kotouče). Hustota elektrického proudu j nemusí být na celé ploše S stejná, proto je nutné integrovat.
Proudovou hustotu j vyjádříme pomocí Ohmova zákona v diferenciálním tvaru:
\[ j = \gamma E_\mathrm{i}, \]kde γ je měrná elektrická vodivost (tzv. konduktivita) a Ei je intenzita elektrického pole na dané plošce dS.
Pro intenzitu elektrického pole Ei platí v případě homogenního pole vztah:
\[ E_\mathrm{i}= \frac{U_\mathrm{i}}{d},\]kde d je vzdálenost a Ui velikost indukovaného napětí na dané vzdálenosti. V této úloze ale nemáme homogenní pole.
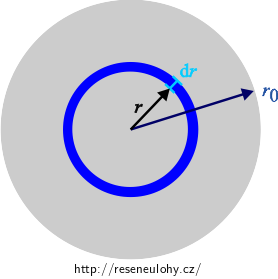
Uvažujeme úzký prstenec o poloměru r a šířce dr a určíme elektrické pole indukované v tomto prstenci. Podle Faradayova zákona elektromagnetické indukce platí:
\[ U_\mathrm{i} = - \frac{\mathrm{d} \Phi}{\mathrm {d}t},\]kde Ui je indukované napětí v prstenci a Φ magnetický indukční tok. Dále můžeme psát:
\[U_\mathrm{i} = - \frac{\mathrm{d} (B S)}{\mathrm {d}t}, \]kde B je magnetická indukce a S je plocha prstence. Plocha S uvnitř prstence je konstantní, tedy:
\[U_\mathrm{i} =- S \frac{\mathrm{d} B}{\mathrm {d}t}=- \pi r^2 \frac{\mathrm{d} B}{\mathrm {d}t}. \]Dosadíme ze zadání za magnetickou indukci B = Bm cos ωt a dostaneme:
\[U_\mathrm{i} = - \pi r^2 \, \frac{\mathrm{d} [B_\mathrm{m} \cos {(\omega t)}]}{\mathrm {d}t} = - \pi r^2 \omega B_\mathrm{m} \sin (\omega t). \]Tím jsme získali indukované napětí v celém prstenci. Protože ale pole podél celého prstence je stejné (situace je symetrická), můžeme velikost intenzity elektrického pole spočítat obdobně ve výše uvedeném případě homogenního pole. Pro intenzitu elektrického pole tedy získáme vztah:
\[ E_\mathrm{i}= \frac{U_\mathrm{i}}{d} = \frac{U_\mathrm{i}}{2 \pi r}= \frac{ \pi r^2 \omega B_\mathrm{m} \sin (\omega t)}{2 \pi r}=\frac{r}{2}\omega B_\mathrm{m} \sin (\omega t).\]kam jsme za délku d dosadili „délku“ prstence 2πr.
Pomocí výše odvozených vztahů můžeme pro hustotu elektrického proudu j psát:
\[ j = \gamma \frac{ r}{2}\omega B_\mathrm{m} \sin (\omega t). \]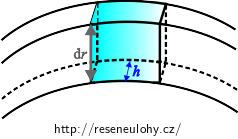
S využitím faktu, že uvažovaný prstenec má obdélníkový průřez o plošném obsahu dS = h dr, můžeme pro celkový proud indukovaný v kotouči psát:
\[ I = \int_\mathrm{S} j \mathrm{d}S = \int_0^\mathrm{r_0} j h \mathrm{d}r= \int_0^\mathrm{r_0} \gamma \frac{ r}{2}\omega B_\mathrm{m} \sin (\omega t) h \mathrm{d}r.\]Výraz zintegrujeme a upravíme:
\[ I = \frac{ \gamma \omega B_\mathrm{m} \sin (\omega t) h} {2}\, \int_0^\mathrm{r_0} r \mathrm{d}r= \frac{ \gamma \omega B_\mathrm{m} \sin (\omega t) h} {2}\, \left[ \frac{r^2}{2}\right]_0^\mathrm{r_0} = \frac{ \gamma \omega B_\mathrm{m} \sin (\omega t) h} {4}\, r^2_0= \frac{ \gamma \omega B_\mathrm{m} h r^2_0 } {4}\, \sin (\omega t). \]Pro časový průběh proudu I platí obecný vztah:
\[ I = I_\mathrm{m} \,\sin (\omega t), \]kde Im je amplituda proudu, která má v tomto případě velikost:
\[I_\mathrm{m} = \frac{ \gamma \omega B_\mathrm{m} h r^2_0 } {4}. \]Řešení – maximální hodnota výkonu
Celkový výkon P spočítáme podobně jako celkový proud I v předchozím oddíle, tedy integrací příspěvků dP jednotlivých prstenců, na které si celý kotouč rozdělíme.
Element výkonu dP proudu indukovaného v prstenci určíme ze vztahu:
\[ \mathrm{d}P=\frac{U_\mathrm{i}^2}{\mathrm{d}R},\]kde dR je odpor tohoto prstence, který lze vypočítat jako:
\[ \mathrm{d}R=\frac{l}{\gamma \mathrm{d}S} = \frac{2 \pi r}{\gamma h \mathrm{d}r} , \]kde l je délka (= obvod) elementárního prstence, γ je vodivost hliníkového prstence, dS = hdr plošný obsah obdélníkového průřezu prstence, h tloušťka prstence a dr je šířka prstence.
Pro indukované napětí Ui jsme v předchozím oddíle odvodili vztah:
\[U_\mathrm{i} = - \pi r^2 \omega B_\mathrm{m} \sin (\omega t). \]Dosadíme do výrazu pro element výkonu dP a upravíme:
\[ \mathrm{d}P=\frac{U_\mathrm{i}^2}{\mathrm{d}R}= \frac{\left[- \pi r^2 \omega B_\mathrm{m} \sin (\omega t)\right]^2}{\frac{2 \pi r}{\gamma h \mathrm{d}r}}= \frac{\pi}{2} \left[\omega B_\mathrm{m} \sin (\omega t)\right]^2 \, \gamma h r^3\, \mathrm{d}r.\]Integrujeme přes celý kotouč:
\[ P = \int \mathrm{d}P = \int_0^\mathrm{r_0} \frac{\pi}{2} \left[\omega B_\mathrm{m} \sin (\omega t)\right]^2 \, \gamma h r^3\, \mathrm{d}r=\frac{\pi}{2} \left[\omega B_\mathrm{m} \sin (\omega t)\right]^2 \, \gamma h \int_0^\mathrm{r_0} r^3\, \mathrm{d}r= \] \[= \pi \left[\omega B_\mathrm{m} \sin (\omega t)\right]^2 \, \gamma h \left[\frac{r^4}{4}\right]_0^\mathrm{r_0}= \frac{\pi}{2} \left[\omega B_\mathrm{m} \sin (\omega t)\right]^2 \, \gamma h \frac{r_0^4}{4}= \frac{ \pi \left[\omega B_\mathrm{m} \right]^2 \, \gamma h r_0^4}{8} \sin^2 (\omega t). \]Maximální výkon Pm můžeme vyjádřit pomocí vztahu:
\[ P = P_\mathrm{m} \sin^2\left(\omega t\right), \] \[ P_\mathrm{m}= \frac{ \pi \left[\omega B_\mathrm{m} \right]^2 \, \gamma h r_0^4}{8}. \]Zápis a číselné dosazení
r0 = 40 mm poloměr hliníkového kotouče h = 1 mm tloušťka hliníkového kotouče B = Bmcos(ωt) závislost magnetické indukce v kotouči na čase Bm = 30 mT maximální hodnota magnetické indukce v kotouči ω = 100π rad/s úhlová frekvence otáčení kotouče Im = ? (A) maximální hodnota indukovaného proudu v kotouči Pm = ? (W) maximální hodnota výkonu v kotouči Z tabulek: γ = 3,7·107 Ω-1m-1
konduktivita hliníku
\[I_\mathrm{m} = \frac{ \gamma \omega B_\mathrm{m} h r^2_0 } {4}= \frac{ 3{,}7 {\cdot} 10^{-7} \cdot 100 \cdot \pi 30 {\cdot} 10^{-3} \cdot 0{,}001 {\cdot} 0{,}04^2} {4}\,\dot=\, 140\,\mathrm A. \]
\[ P_\mathrm{m}= \frac{ \pi [\omega B_\mathrm{m} ]^2 \, \gamma h r_0^4}{8}=\frac{ \pi \cdot[100 \cdot \pi \cdot 30 {\cdot} 10^{-3} ]^2 {\cdot} 3{,}7 {\cdot} 10^{-7} \cdot 0{,}001 {\cdot} 0{,}04^4}{8} \,\dot=\, 330\,\mathrm W. \]
Odpověď
Indukovaný proud v kotouči dosahuje maximální hodnoty přibližně 140 A a jeho maximální výkon je asi 330 W.