Sbírka řešených úloh

Okamžité hodnoty napětí a proudu v sériovém RLC obvodu

Úloha číslo: 77

Sériový obvod střídavého proudu je tvořen rezistorem o odporu 90 Ω, cívkou o indukčnosti 1,3 H a kondenzátorem o kapacitě 10 μF. Obvod je připojen ke zdroji střídavého napětí o amplitudě 100 V a frekvenci 50 Hz. Napište rovnice pro okamžité hodnoty napětí a proudu v obvodu, jestliže počáteční fáze proudu je nulová.

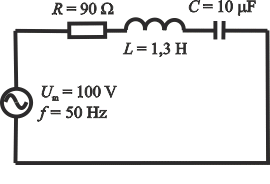
• Zápis

  Ze zadání si vypíšeme veličiny, které známe:

  Amplituda zdroje střídavého napětí v obvodu	Um = 100 V
  Frekvence zdroje střídavého napětí	f  = 50 Hz
  Odpor rezistoru	R = 90 Ω
  Indukčnost cívky	L = 1,3 H
  Kapacita kondenzátoru	C = 10 μF
  Počáteční fáze proudu	φ0i = 0

  Veličiny, které chceme určit:

  Okamžitá hodnota proudu	i(t) = ? (A)
  Okamžitá hodnota napětí	u(t) = ? (V)

• Nápověda 1

  Průběh střídavého proudu a střídavého napětí lze popsat pomocí funkce sinus.

  Vyhledejte si rovnice, kterými popisujeme okamžité hodnoty střídavého napětí a proudu.

• Nápověda 2

  Pro vyčíslení hledaných rovnic potřebujeme znát amplitudu proudu I_m a fázový posun mezi napětím a proudem φ_0u. K jejich určení použijeme Ohmův zákon pro střídavý proud.

  V úloze Sériový RLC obvod najdete podrobné vysvětlení výpočtu proudu a odvození fázového posunu.

• Vyjádření amplitudy proudu I_m

  Použijeme Ohmův zákon pro obvod se střídavým proudem:

  \[I_\mathrm{m}=\frac{U_\mathrm{m}}{Z}=\frac{U_\mathrm{m}}{\sqrt{R^2+\left(X_L-X_C\right)^2}}=\frac{U_\mathrm{m}}{\sqrt{R^2+\left(2 \pi f L - \frac{1}{2 \pi f C}\right)^2}} \]

  ---

  Číselné vyjádření:

  \[I_\mathrm{m}=\frac{100}{\sqrt{90^2+\left(2 \pi \cdot 50 {\cdot} 1{,}3 - \frac{1}{2 \pi \cdot 50 {\cdot} 10 \cdot 10^{-6}}\right)^2}} \, \mathrm{A} \] \[I_\mathrm{m} \,\dot{=}\, 0{,}79 \, \mathrm{A}\]

• Vyjádření fázového posunu mezi napětím a proudem φ_0u

  Použijeme vzorec pro vyjádření fázového posunu pomocí impedancí jednotlivých prvků:

  \[ \mathrm{tg\,} \varphi_\mathrm{0u} = \frac{X_\mathrm{L} - X_\mathrm{C}}{R}= \frac{\omega L- \frac{1}{ \omega C}}{R}= \frac{2 \pi f L- \frac{1}{ 2 \pi f C}}{R} \] \[\varphi_\mathrm{0u} = \mathrm{arctg\,}\left(\frac{2 \pi f L- \frac{1}{ 2 \pi f C}}{R}\right)\]

  ---

  Číselné řešení:

  \[\varphi_\mathrm{0u} = \mathrm{arctg\,}\left(\frac{2 \pi f L- \frac{1}{ 2 \pi f C}}{R}\right)= \mathrm{arctg\,}\left(\frac{2\pi \cdot 50 {\cdot} 1{,}3 - \frac{1}{ 2 \pi \cdot 50 {\cdot} 10 \cdot 10^{-6}}}{90}\right)\] \[\varphi_\mathrm{0u} \,\dot{=}\, 45 ^{\circ} = \frac{\pi}{4} \]

• Okamžité hodnoty střídavého proudu a napětí

  Okamžitá hodnota střídavého proudu:

  Fázový posun proudu je nulový, amplitudu proudu I_m jsme vypočítali:

  \[ i(t)=I_\mathrm{m} \, \sin(\omega t + \varphi_{0i})=I_\mathrm{m}\, \sin( 2 \pi f t + \varphi_{0i} ) \] \[ i(t)\,\dot{=}\,0{,}79 \cdot \sin(2 \pi 50 t)\,\mathrm A =0{,}79 \cdot \sin(100 \pi t)\,\mathrm A.\]

   

  Okamžitá hodnota střídavého napětí:

  Amplitudu napětí U_m známe, fázový posun jsme vypočítali:

  \[ u(t)=U_\mathrm{m} \, \sin(\omega t + \varphi_\mathrm{0u})=U_\mathrm{m} \, \sin( 2 \pi f t + \varphi_\mathrm{0u} ) \] \[u(t)\,\dot{=}\,100 \cdot \sin( 2 \pi 50 t + \frac{\pi}{4} )\,\mathrm V = 100\cdot \sin( 100 \pi t + \frac{\pi}{4} )\,\mathrm V.\]

   

  Do vztahů dosazujeme číselné hodnoty času vyjádřené v sekundách.

• Odpověď

  Rovnice pro okamžité hodnoty napětí a proudu v sériovém RLC obvodu se střídavým proudem mají přibližně tvar:

  \[ i(t)=0{,}79 \cdot \sin\left({100 \pi t}\right)\,\mathrm A,\] \[u(t)=100 \cdot \sin\left( 100 \pi t + \frac{\pi}{4} \right)\,\mathrm V. \]